力扣：2322. 从树中删除边的最小分数

存在一棵无向连通树，树中有编号从 0 到 n - 1 的 n 个节点， 以及 n - 1 条边。

给你一个下标从 0 开始的整数数组 nums ，长度为 n ，其中 nums[i] 表示第 i 个节点的值。另给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [ai, bi] 表示树中存在一条位于节点 ai 和 bi 之间的边。

删除树中两条 不同 的边以形成三个连通组件。对于一种删除边方案，定义如下步骤以计算其分数：

1. 分别获取三个组件 每个 组件中所有节点值的异或值。
2. 最大 异或值和 最小 异或值的 差值 就是这一种删除边方案的分数。

• 例如，三个组件的节点值分别是：[4,5,7]、[1,9] 和 [3,3,3] 。三个异或值分别是 4 ^ 5 ^ 7 = 6、1 ^ 9 = 8 和 3 ^ 3 ^ 3 = 3 。最大异或值是 8 ，最小异或值是 3 ，分数是 8 - 3 = 5 。

返回在给定树上执行任意删除边方案可能的 最小 分数。

示例 1：

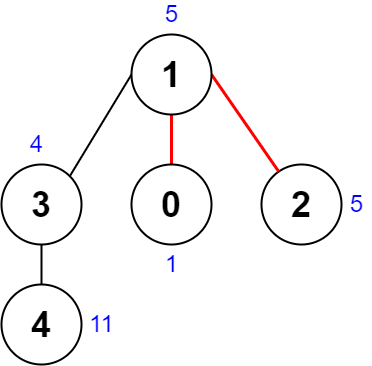
输入：nums = [1,5,5,4,11], edges = [[0,1],[1,2],[1,3],[3,4]]
输出：9
解释：上图展示了一种删除边方案。
- 第 1 个组件的节点是 [1,3,4] ，值是 [5,4,11] 。异或值是 5 ^ 4 ^ 11 = 10 。
- 第 2 个组件的节点是 [0] ，值是 [1] 。异或值是 1 = 1 。
- 第 3 个组件的节点是 [2] ，值是 [5] 。异或值是 5 = 5 。
分数是最大异或值和最小异或值的差值，10 - 1 = 9 。
可以证明不存在分数比 9 小的删除边方案。

示例 2：

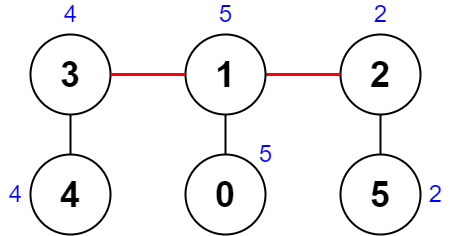
输入：nums = [5,5,2,4,4,2], edges = [[0,1],[1,2],[5,2],[4,3],[1,3]]
输出：0
解释：上图展示了一种删除边方案。
- 第 1 个组件的节点是 [3,4] ，值是 [4,4] 。异或值是 4 ^ 4 = 0 。
- 第 2 个组件的节点是 [1,0] ，值是 [5,5] 。异或值是 5 ^ 5 = 0 。
- 第 3 个组件的节点是 [2,5] ，值是 [2,2] 。异或值是 2 ^ 2 = 0 。
分数是最大异或值和最小异或值的差值，0 - 0 = 0 。
无法获得比 0 更小的分数 0 。

提示：

• n == nums.length
• 3 <= n <= 1000
• 1 <= nums[i] <= 108
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• edges 表示一棵有效的树

---

前置概念：利用异或的自反性和归零律—— 本质上，“去除某部分” 在异或中等价于 “对该部分再异或一次”（两次异或同一内容会相互抵消）。

分析：

        对于题目描述的一棵无向连通树，我们要切割其2条边，将整棵树划分为3部分，同时还要获取这3部分的异或总值。通过上述的概念不难推出，在一棵树上去除一子树求剩下部分的异或就同于将整棵树的异或总值与去除部分的异或总值再进行一次异或，举个例子：在例1中，[1,3,4]=[0,1,2,3,4]⊕[0]⊕[2]，换句话说，以1结点为根的树上异或总值 与 以2结点为根的树上异或总值 进行异或就是剩下部分的异或总值。因此，我们就需要设置一个数组 sum[] 用于存储以 i 结点为根的子树其树上异或总值（0<=i<=n-1）。

        想到这里还不够，如果例1中需要剪切的边是[1,3]和[3,4]该怎么处理？？？结点3是一个子树的根，而结点4又是子树的一部分，这时候要是还按照上述的算法:                       

sum[1]⊕sum[3]⊕sum[4] 又 sum[3]=sum[4]⊕nums[3]

->sum[1]=sum[4]⊕sum[4]⊕nums[3] ->sum[1]=nums[3]

说明剪切[1,3]与[3,4]后剩下结点1为根的部分的异或总值就为结点3的nums值

而剪切[1,3]与[3,4]后剩下结点1为根的部分的异或总值应为 sum[1]⊕sum[3]

说明在计算不同部分的异或值时，需要判断剪切后每部分的根结点之间是否存在 父节点-子节点 的关系。而这时候就需要引入 dfs序 ，从根节点向下 dfs 并给每个结点编号并存入dfn[]数组中，同时定义 ch[] 表示以dfs序为i的结点其子树长度。这样一来，假设经过剪切后一部分的根节点为i，另一部分的根节点为j，i子树的dfs序列区间即为 [dfn[i]，dfn[i]+ch[i]-1]，如果dfn[j]位于这个区间就说明结点 j 位于 i子树内。

        随后，各个数组处理完之后就要开始选择切割的边了，因为要获取删除边的最小分数，一条边与另一条边两两组合然后枚举出所有情况是不可避免的。假设我们选取的2条边为 e1，e2 ，切割2条边将得到3个部分，对于切割的2条边选择向下取点（取边两端dfn值较大的那个结点），这样正好可以取到切割出去子树的根节点。 之后就判断 父节点-子节点关系然后计算结果就行了。       

在本题中为什么选用dfs序列？

由于题目给出的是无向树，通过dfs序列可以将整棵树重新编号，原本输入的边u,v不明确，通过dfs序列的重新编号可以清晰地理出树结构方便后续计算；在计算不同部分的异或值时，dfs序列可以实现父节点-子节点关系的快速判断；在切割后，利用dfs序列可以快速获取切割出去那部分的根节点从而获取异或值。

AC代码：

C++版本：

class Solution {
public:static const int N = 1e3 + 10;static const int INF = 0x3f3f3f3f;vector<int> a[N];int ch[N];//以 dfs序为i的结点 为根，其子树（包含根）的长度int dfn[N];//i结点的dfs序int xor1[N];// 以 dfs序为i的结点 为根，其子树（）包含根的异或总值int ans = INF;int n = 1;void init() {memset(dfn, 0, sizeof dfn);memset(ch, 0, sizeof ch);memset(xor1, 0, sizeof xor1);}int minimumScore(vector<int>& nums, vector<vector<int>>& edges) {init();for (auto it : edges) {int u = it[0];int v = it[1];a[u].push_back(v);a[v].push_back(u);}dfs(0,nums);//因为是无向树，默认从结点0进入//遍历所有的边，枚举所有可能for (int i = 0;i < edges.size()-1;i++) {int u1 = dfn[edges[i][0]], v1 = dfn[edges[i][1]];int al = max(u1, v1);//在边的两端取结点dfs序中较大者for (int j = i + 1;j < edges.size();j++) {int u2 = dfn[edges[j][0]], v2 = dfn[edges[j][1]];int bl = max(u2, v2);//获取2条边的dfs序较大者int pre = min(al, bl);//2个dfs序中较小者int pos = max(al, bl);//2个dfs序中较大者int p, q, r;//3个部分的异或值if (pos <= (pre + ch[pre] - 1)) {//pos在pre的子树上p = xor1[pos];q = xor1[pre]^xor1[pos];r = xor1[1] ^ xor1[pre]; }else {p = xor1[pos];q = xor1[pre];r = xor1[1] ^ p ^ q;}int t = min(min(q, p), r);int k = max(max(q, p), r);ans = min(ans, k - t);}}return ans;}void dfs(int x, vector<int>& nums) {int idx = n;//将当前状态的dfs序号寄存于idx中ch[idx] = 1;dfn[x] = idx;  xor1[idx] = nums[x];n++;for (auto it : a[x]) {//访问结点x的所有邻接结点if (dfn[it] == 0) {//邻接结点的dfs序列未编辑（邻接结点未访问）dfs(it,nums);xor1[idx] ^= xor1[dfn[it]];ch[idx] += ch[dfn[it]];}}}
};

java版本：

import java.util.ArrayList;
import java.util.Arrays;class Solution {static final int INF=1000000000;static final int N=1010;int[] dfn=new int[N];int[] ch=new int[N];int[] xor=new int[N];int n=1;ArrayList<Integer>[] a=new ArrayList[N];void init(){Arrays.fill(dfn,0);Arrays.fill(ch,1);}public int minimumScore(int[] nums, int[][] edges) {init();int ans=INF;for (int i = 0; i < nums.length; i++) {a[i]=new ArrayList<>();}for (int i = 0; i < edges.length; i++) {int u=edges[i][0];int v=edges[i][1];a[u].add(v);a[v].add(u);}dfs(0,nums);for (int i = 0; i < edges.length-1; i++) {int u1=dfn[edges[i][0]],v1=dfn[edges[i][1]];int al=Math.max(u1,v1);for (int j = i+1; j < edges.length; j++) {int u2=dfn[edges[j][0]],v2=dfn[edges[j][1]];int bl=Math.max(u2,v2);int pre=Math.min(al,bl);int pos=Math.max(al,bl);int p,q,r;if(pos<=pre+ch[pre]-1){p=xor[pos];q=xor[pre]^xor[pos];r=xor[1]^xor[pre];}else{p=xor[pos];q=xor[pre];r=xor[1]^p^q;}int t=Math.min(Math.min(p,q),r);int k=Math.max(Math.max(p,q),r);ans=Math.min(ans,k-t);}}return ans;}public void dfs(int x,int[] nums){int idx=n;dfn[x]=idx;xor[idx]=nums[x];n++;for (int i = 0; i < a[x].size(); i++) {int v=a[x].get(i);if(dfn[v]==0){dfs(v,nums);xor[idx]^=xor[dfn[v]];ch[idx]+=ch[dfn[v]];}}}
}