当前位置：首页 > news >正文

论文Review Registration VGICP | ICRA2021 | 经典VGICP论文

news 2025/9/6 8:35:42

基本信息

题目：Voxelized GICP for Fast and Accurate 3D Point Cloud Registration

来源：ICRA2021

学校：日本国家先进工业科学技术研究院

是否开源：https://github.com/koide3/fast_gicp

https://github.com/koide3/small_gicp

摘要：GICP、VGICP

本文提出了一种快速精确的三维点云配准的体素化广义迭代最近点( VGICP )算法。该方法扩展了基于体素化的广义迭代最近点( GICP )方法，在保持精度的同时避免了代价高昂的最近邻搜索。与从点位置计算体素分布的正态分布变换( NDT )不同，我们通过聚合体素中每个点的分布来估计体素分布。体素化方法允许我们高效地并行处理优化，所提出的算法可以在CPU上运行30 Hz，在GPU上运行120 Hz。通过在模拟和真实环境中的评估，我们证实了所提算法的精度与GICP相当，但明显快于现有方法。这将有助于开发实时三维LIDAR应用，这些应用要求对LIDAR帧之间的相对位姿进行极快的评估。

Introduction

三维点云配准是许多三维激光雷达（LIDAR）应用中的核心任务，例如校准、定位、地图构建和环境识别。点云配准的目标是将两组点云（通常是源点云和目标点云）对齐，找到它们之间的空间变换（旋转和平移）。目前，两种流行的点云配准方法是：

广义迭代最近点（GICP） GICP是对经典迭代最近点（ICP）算法的扩展，通过分布到分布（distribution-to-distribution）的比较方式提高配准精度。GICP假设点云中的点具有局部协方差结构，利用这些分布信息进行更精确的点对齐。
正态分布变换（NDT） NDT通过体素化（voxelization）方法避免了昂贵的最近邻搜索，从而提高处理速度。它将点云分割成体素网格，为每个体素中的点拟合正态分布，然后通过最大化点在这些分布下的似然来对齐点云。

两种方法的局限性

GICP的局限性： GICP依赖于最近邻搜索来关联点对，这在点云规模较大时计算成本高，尤其在计算资源有限的设备上难以实现实时处理。此外，最近邻搜索涉及大量条件分支，不适合在GPU上优化。
NDT的局限性： NDT的性能高度依赖于体素分辨率的选择。体素分辨率需要根据环境和传感器特性进行仔细调整。如果分辨率选择不当，NDT的配准精度会显著下降。

论文提出的解决方案

论文提出了一种新的算法——Voxelized GICP（VGICP），结合了GICP的高精度和NDT的高效体素化方法。VGICP通过体素化技术实现并行计算，显著提高了处理速度，同时通过多点分布聚合方法（multi-point distribution aggregation）增强了对体素分辨率变化的鲁棒性。VGICP能够在CPU上以30Hz、GPU上以120Hz的速率处理包含15,000个点的点云。

论文的主要贡献

多点分布聚合方法：提出了一种从体素内少量点中稳健估计体素分布的方法，使得算法对体素分辨率变化更鲁棒。
VGICP算法：提出了一种兼具GICP精度和更高处理速度的点云配准算法。
公开实现：提供了VGICP和并行化GICP的开源实现，供研究社区使用。

Related Works

A. GICP

GICP是经典ICP算法的变种之一。经典ICP通过迭代寻找点对并最小化点间距离来对齐点云，而GICP通过分布到分布的匹配方式改进了精度。它假设每个点具有局部协方差矩阵，并利用这些分布信息进行更精确的对齐。然而，GICP依赖于最近邻搜索（通常使用KD树），这在点云规模较大时成为计算瓶颈。此外，最近邻搜索的条件分支使其不适合GPU优化。

B. NDT

NDT通过体素化避免了最近邻搜索的开销。它将点云分割成体素网格，为每个体素中的点拟合正态分布，然后通过最大化点在这些分布下的似然来对齐点云。NDT的变种D2D-NDT（分布到分布NDT）对源点云和目标点云都进行体素化，并计算体素分布之间的距离，其精度优于经典NDT。然而，NDT的精度对体素大小敏感，需根据环境和传感器特性仔细调整体素分辨率。一些改进方法（如多分辨率NDT和三线性体素平滑）试图增强鲁棒性，但以牺牲处理速度为代价。

C. 基于特征的配准

基于特征的配准方法首先从点云中提取关键特征（如平面、边缘、FPFH、SHOT等），然后通过特征对应估计变换。这些方法对初始位姿误差较为鲁棒，有些甚至无需初始猜测。然而，由于仅使用有限数量的特征，基于特征的方法精度通常低于基于点的配准方法（如GICP或NDT）。在实际应用中，通常先使用基于特征的方法进行粗配准，再结合基于点的精细配准。

D. 基于深度神经网络的配准

近年来，深度神经网络在点云配准领域受到关注。一些工作提出网络提取局部鲁棒描述符，另一些则直接回归点云间的相对位姿。这些方法在噪声和初始位姿误差方面表现鲁棒，并能利用GPU加速。然而，其配准精度通常不如传统几何方法（如GICP）。因此，深度学习方法常与基于点的配准方法结合使用，例如在激光雷达里程计估计中结合ICP进行精化。

Method

A. GICP algorithm

GICP（Generalized Iterative Closest Point）是经典ICP算法的扩展，它将点云配准问题建模为分布到分布的匹配，而不是简单的点到点距离最小化。这部分回顾了GICP的核心数学框架，为后续VGICP的扩展奠定基础。

B. Voxelized GICP algorithm

VGICP通过体素化（voxelization）扩展GICP，避免最近邻搜索的瓶颈，同时引入一对多分布对应，以提高对体素分辨率的鲁棒性。核心是平滑目标分布，并使用体素聚合点分布。

C. Implementation

实验

硬件平台

硬件：Intel Core i9-9900K CPU 和 NVIDIA GeForce RTX 2080 Ti GPU。

数据集

Benchmark

结果分析

精度结果：
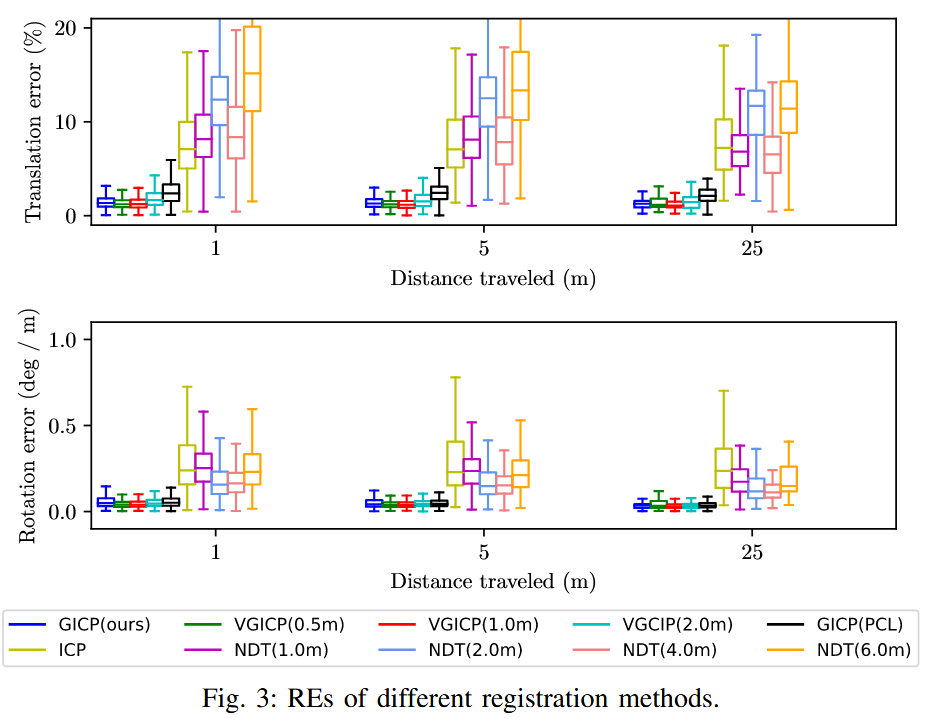
- 图3展示了不同方法的RE（相对误差）。NDT的精度高度依赖体素分辨率：在1m、2m、6m分辨率下精度显著下降，最优为4.0m，但仍无法捕捉环境细部，导致整体精度低于GICP。
- 表格I展示了ATE（绝对轨迹误差）。GICP类算法（包括VGICP）优于经典ICP。论文的GICP和VGICP实现略优于PCL的GICP，可能因使用高斯-牛顿优化器（Gauss-Newton）而非PCL的BFGS优化器（更快、更精确）。
- VGICP的关键优势：对体素分辨率变化鲁棒。即使体素内点数少，也能生成有效分布（前文多点分布聚合方法），导致在宽范围分辨率下性能一致。结果显示VGICP精度与GICP相当，且优于NDT。
速度结果：
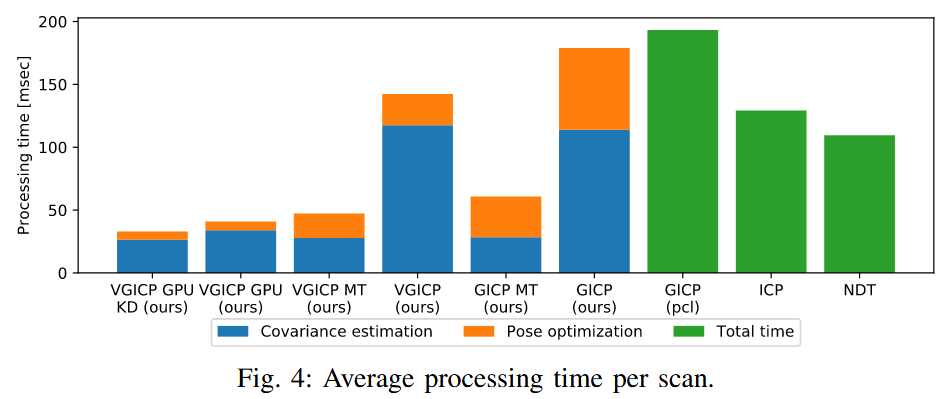
- 图4展示了平均处理时间。
  - 单线程：论文GICP（189ms）、VGICP（156ms）快于PCL GICP（201ms）。预处理（协方差估计）相同，但VGICP的位姿优化因体素化而加速。
  - 多线程：GICP（68ms）、VGICP（50ms），进一步加速。
  - GPU版本VGICP：仅6ms，极快。GPU蛮力最近邻搜索虽在该硬件上慢于CPU KD树，但适合低端CPU+高端GPU（如NVIDIA Jetson）。
- 启示：在目标点云不频繁变化的场景（如关键帧里程计），VGICP效率更高。

评价

模拟环境实验验证了VGICP的精度（媲美GICP）和鲁棒性（对体素分辨率不敏感），解决了NDT的弱点。速度提升显著，支持实时应用。自定义模拟器的真实性增强了结果的可信度，但模拟环境可能忽略真实噪声（如传感器误差），需结合真实环境验证。

评价

真实环境实验确认了模拟结果：VGICP精度高（媲美GICP）、速度快（GPU下极致）、鲁棒强（分辨率变化小影响）。数据规模（15,000点/帧）和轨迹长度（120m）接近实际应用（如自动驾驶）。真值使用GICP可能略偏向GICP类方法，但结果一致性高。局限：仅评估连续帧配准，未涉及大初始误差或动态环境。