机器学习基础-day03-机器学习中的线性回归
1 求导法则
为什么要学习微积分？
在机器学习和深度学习中，需要衡量预测的结果和实际结果的一个差异，使用一个叫损失函数的数学打分器比对。损失函数越小，表示结果预测的准；损失函数越大表示结果预测的不准。
比如，如果我们预测明天下雨的概率是80%，但实际上明天是晴天，那么我们的预测就不准，损失函数的值就会比较高。反之，如果我们预测明天下雨的概率是5%，而明天确实是晴天，虽然我们还是预测错了，但相对来说，我们预测得“更接近”实际情况，所以损失函数的值就会低一些。
损失函数在机器学习和深度学习中非常重要，因为它指导着模型的学习过程，让模型知道应该如何调整自己的参数，以便更好地预测未来的结果。
在机器学习或者深度学习中，绝大部分任务是构建一个损失函数，然后使其最小化，这个优化的过程就是微分。
1.1 导数
导数即在连续不间断的线性函数某个点的切线斜率。导数是函数，如果把每个点的斜率都用一个函数表示，这个函数就是“导函数”，通常叫为“导数”。
导函数表示的切线集合可以描述：
函数的整体变化趋势
也可以表示部分的变化趋势
还可以表示某个点的变化趋势
1.2 斜率的极值和最值
如果上面的图像是损失函数，那么斜率为0的点可能就是损失函数最小值或最大值。
极小值/极大值：局部范围的极值。
最小值/最大值：全局的极值。
2 前向传播
前向传播是指在一个机器学习算法中，从输入到输出的信息传递过程，具体来说，就是在数据输入后，经过一系列的运算后得到结果的过程。
输入x 经过一系列计算f(x) 得到y的过程
比如y=2x+3,这个公式，前向传播就是通过给定x,根据公式2x+3得到输出结果y的值的过程就是前向传播。
对数据的输入逐步处理，提取对应的特征，并进行预测。
前向传播流程：
输入→前向计算→单点误差→均方误差
2.1 输入
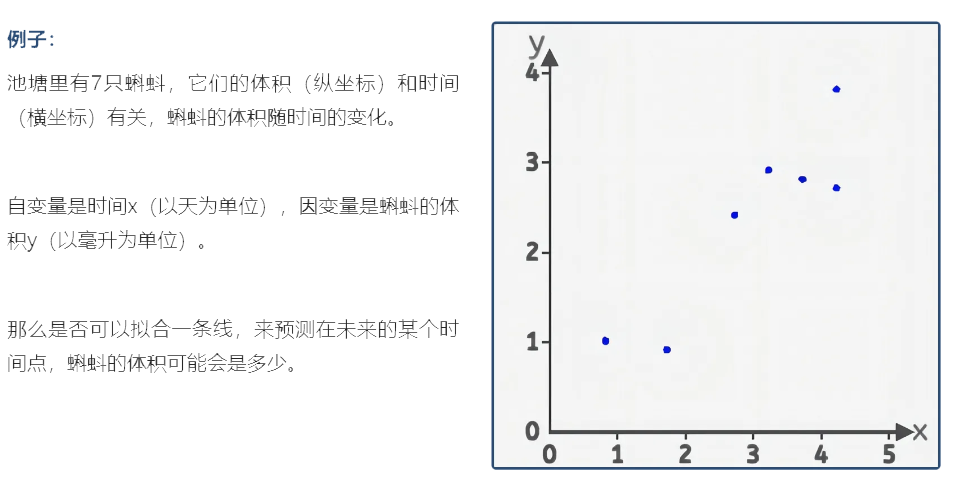
2.2 前向计算
前向传播是指在一个机器学习算法中，从输入到输出的信息传递过程，具体来说，就是在数据输入后，经过一系列的运算后得到结果的过程。
在本实验中，为了使用直线来拟合上面7个散点，可以用直线的斜截式方程来进行拟合，给出直线公式：y=wx+b
刚开始接触，所以限制了w和b的范围：
在前向计算中，为了简化运算，我们固定b的值为0，而w的值可以任意修改（范围0-2）。
w（weight）：权重
b（bias）：偏置
也就是说，我们是用一条过原点的直线来拟合这些散点，在该组件中修改w的值可以实时看到直线与散点的位置关系。
2.3 单点误差
由下图可知，当w等于2的时候 "拟合" 这些散点的效果并不好，和实际的坐标点y轴有一些差距。
目标获得每一个数据点损失。
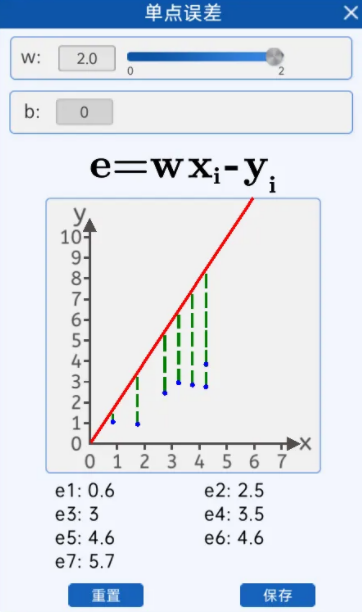绿色的虚线是x相同时，预测值
和真实值y的差（分正负）
2.3 均方误差
损失函数的概念：
损失函数（Loss Function）是用来衡量模型预测结果与实际结果之间的差异的一种函数。在机器学习中，损失函数通常被用来优化模型，通过最小化损失函数来提高模型的预测准确率。
3 前向传播的过程
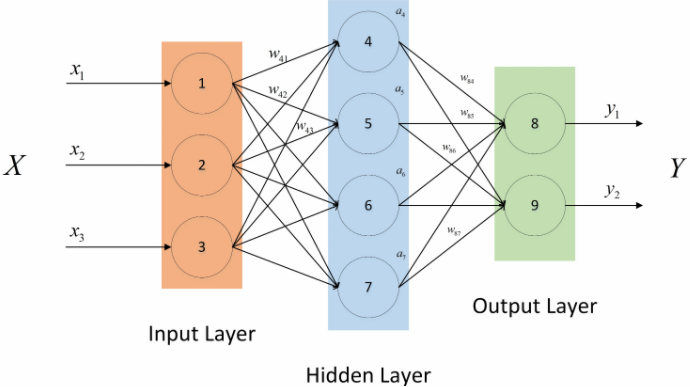
step1：输入层
输入数据首先需要进入输入层，每一个神经元都会接收一个信号(输入值(矩阵))
在本例中输入就是x
step2：输入层到隐藏层
输入层的输出作为下一层的(通常是隐藏层)，通过与权重相乘加上偏置项后进行非线性变换，使用激活函数对隐藏层的输出进行非线性变换，以引入非线性特性，增强模型的表达能力。
在本例中w就是特征。
step3：隐藏层到输出层
将隐藏层的输出乘以隐藏层到输出层的权重矩阵，再加上偏置，计算输出层的输出。
在本例中输出就是y
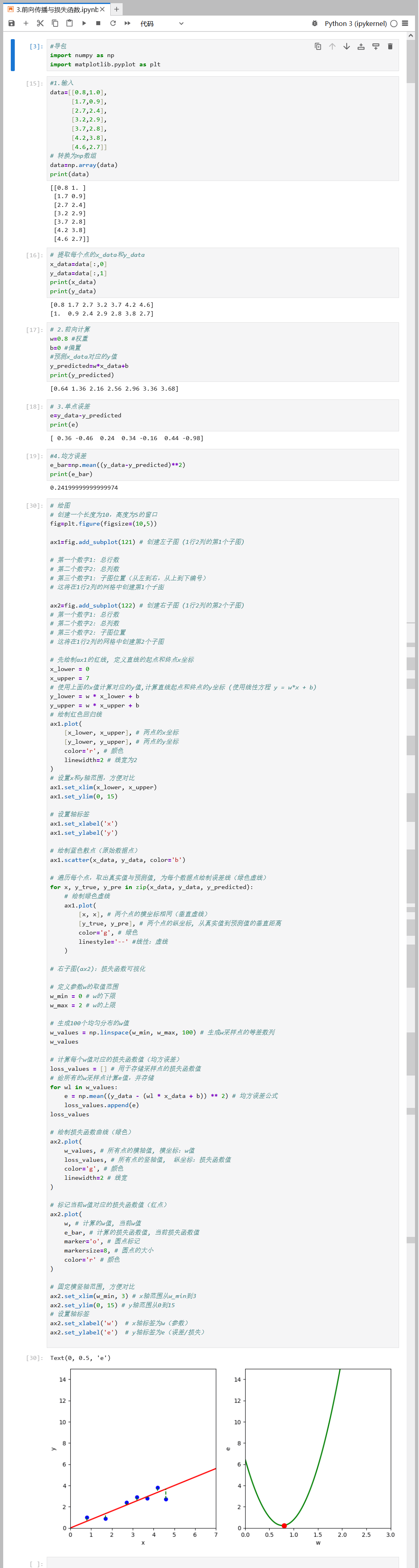
代码运行：使用JupyterLab
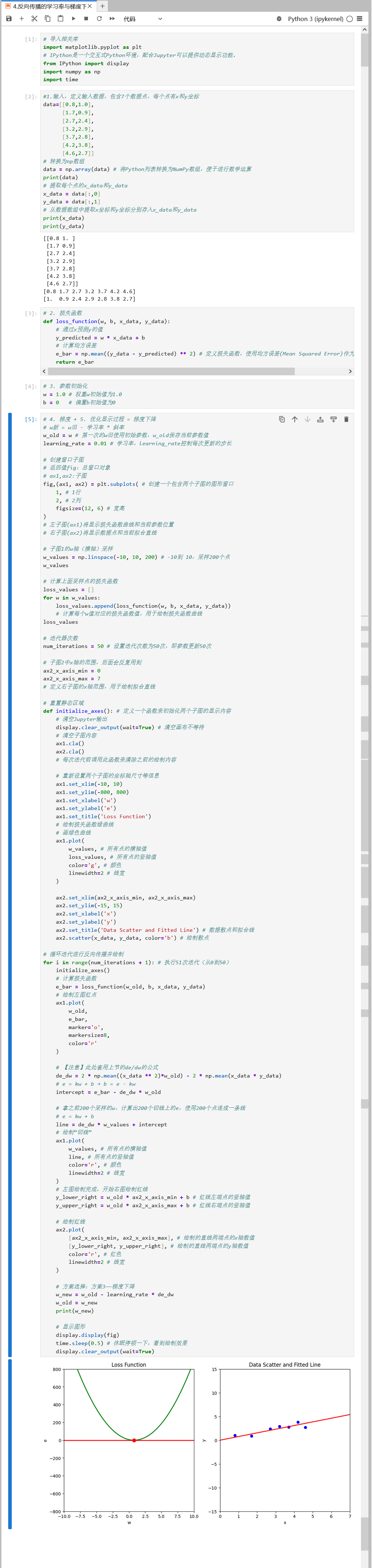
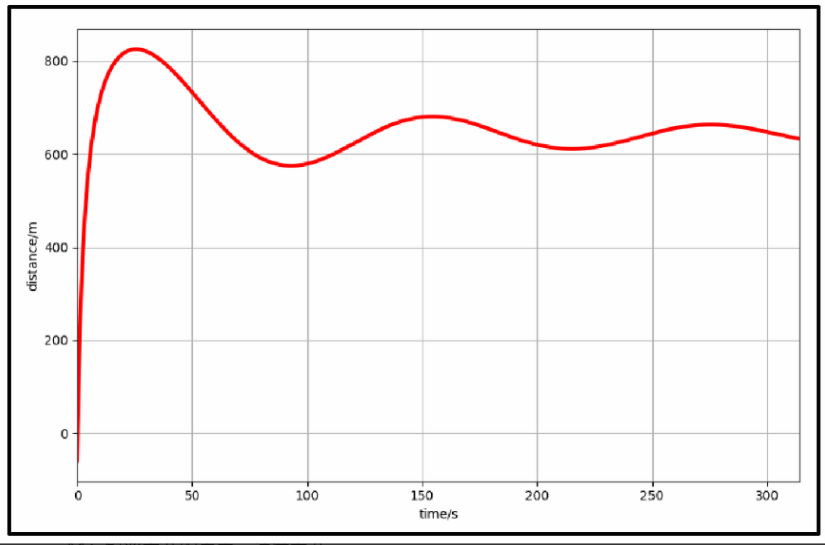
4 反向传播的学习率与梯度下降
依据蝌蚪案例，在上述前向传播过程中， 我们已经 “拟合” 出了一条直线来描述时间与蝌蚪体积之间的关系， 但令损失函数
值最小的直线是我们一次次通过手动修改参数w值得到的。而我们希望在随便输入一个参数后，这个参数可以根据 “我们的期望” 去 “自动修改”，而不是耗费人力来不断修改参数。 基于此，有了反向传播这个过程。
4.1 前向传播与反向传播的区别
前向传播是在参数固定后，向公式中传入参数，进行预测的一个过程。当参数值选择的不恰当时，会导致最后的预测值不符合我们的预期，于是我们就需要重新修改参数值。在前向传播实验中时，我们都是通过手动修改w值来使直线能更好的拟合散点。
反向传播是在前向传播后进行的，它是对参数进行更新的一个过程，反向传播的过程中参数会根据某些规律修改从而改变损失函数的值。
代码流程：
输入→损失函数→参数初始化→梯度→优化过程显示
4.2 损失函数
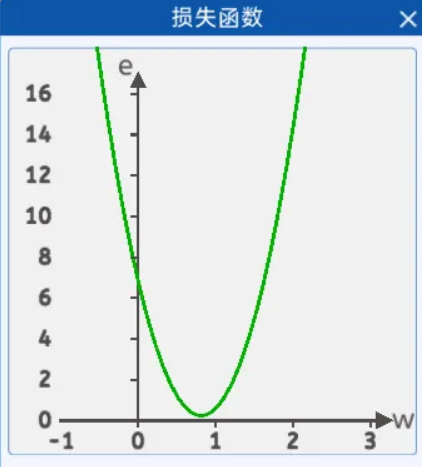
给出直线公式y=wx+b，令 b=0。在前向传播时，得到均方差损失函数，根据该表达式，可以发现，损失函数是一个关于w的一元二次方程：
4.3 参数初始化
反向传播自己会不断的修改参数，即w，那么刚开始时，需要给w一个初始化的值(这个初始化的值可以是任意的值)，初始化方式可以有随便给一个数或者让代码随机定一个，后续损失的值会根据优化算法来更新w。
4.4 梯度+优化过程显示=梯度下降
4.4.1 优化方法（优化器）
在损失函数关于w的表达式中，确实存在一个w，使得损失函数的值最小。下面使用三种方案，包括固定值法、斜率法、小固定值*斜率法，展示一下其不同的优化效果。
4.4.1.1 固定值法
在更新w的时候，采用旧的w减去一个固定的值的方法其公式如下所示：
固固定值的弊端有两个：
1. 方向性不确定
当固定值的正负确定后，就意味着w的更新方向确定了，比如w>0时，且固定值为正数时，w的值是不断减小的，w<0时，固定值为负数时，w的值是不断变大的。
2. 准确性不佳
不能够准确的更新到令损失值最小的w值，比如最合适的w值为0.8，现在的w值为1，而固定值为0.5，那么就会跳过0.8，直接变成0.5，并且如果还没迭代完，还会变成0，-0.5，…。
也就是说，想通过该方法更新到最好的w值，要么事先算好，要么碰运气，总之效果很差。
4.4.1.2 斜率法
在这里它就是损失函数曲线中的w点的切线，斜率还有个很好的特性，那就是当w小于最低点对应的w时，它是负的；当w大于最低点对应的w时，它是正的。
在迭代w的过程中，分为两种情况：
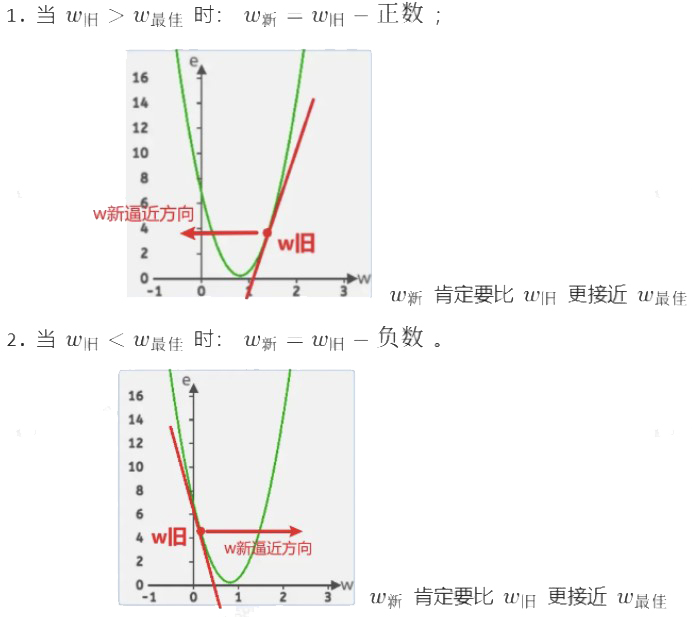
如果只考虑斜率正负号，整合公式：
斜率法的弊端：
当损失函数比较陡峭时，斜率值很大，会来回震荡，并且斜率值越来越大，损失函数值也会越来越大，效果也不是很理想。
4.4.1.3 小固定值*斜率（着重了解）
斜率有很好的特性，但是斜率值太大了不受控制，那么是不是可以把斜率，也就是梯度的值乘以一下很小的数（小于1）。其公式如下所示：
式子中的小固定值被称为学习率，通过改变学习率的值能调整w的更新速度，而整个式子就叫做梯度下降（Gradient Descent，GD），是一种优化函数，作用是最小化损失函数。
4.4.2 学习率（Learning Rate）
在机器学习和深度学习中，学习率是一个超参数，用于控制权重(w)更新的速度。通常来说，学习率越大，参数更新就越快，模型就学习的越快，但如果学习率过大，模型可能会不稳定，甚至无法收敛到最优解。学习率越小，参数更新就越慢，模型学习的就越慢，但如果学习率过小，模型可能在有限的时间下无法找到最优解。
4.4.3 梯度
在机器学习中，梯度表示损失函数对于模型参数的偏导数，梯度下降是机器学习中一种常用的优化算法。
它的基本思想是在训练过程中通过不断调整参数，使损失函数（代表模型预测结果与真实结果之间的差距）达到最小值。
为了实现这一目标，梯度下降算法会计算损失函数的梯度（带方向的斜率），然后根据梯度的方向更新权重，使损失函数不断减小。
对于一个模型来说，我们可以计算每一个权重对损失函数的影响程度，然后根据损失函数的梯度来更新这些权重。通过不断重复这一过程，我们就可以找到一组使损失函数最小的权重值，从而训练出一个优秀的模型。
什么是梯度？
在机器学习中，梯度是一个向量，表示函数在某一点处沿着各个方向的变化率，即函数在某一点上的方向导数沿着该方向取得最大值。简单来说，梯度指向函数增长最快的方向，而负梯度指向函数下降最快的方向。
梯度下降过程：
1.初始化参数w和b（通常是随机值或零）
2.前向传播：使用当前参数计算预测值
3.计算损失：比较预测值和真实值
4.反向传播：计算损失函数对各个参数的梯度
5.参数更新：沿着负梯度方向更新参数
代码运行流程：
