在线性代数里聊聊word embedding

最近在复习线性代数，学到线性相关、线性无关和向量空间这里，突然想到word embedding训练出来的向量是什么样呢？是否满秩？是n维空间中的m维向量（m<=n吗？）

涉及概念：正交向量、正交矩阵、线性相关与线性无关、单位矩阵、秩、向量组······（哈哈哈像我一样忘了的同学可以去理解一下）

撰写此文的初衷是对于矩阵计算如果没有形状的话会不太号想象，所以实际化一些，便于理解~

1、one-hot独热编码

一个非常非常常见的嘉宾——one-hot!!!!

可以说他是word embedding之间的一个常用手段，将每个词都变成互相正交的向量。

如果有n个词（n维），那么每个向量就有n-1个0和1个1（能懂吗？？能懂吗？？？）

每个向量都是正交的，张成一个n维空间。

也可以这么想，这个向量组可以组成一个单位矩阵E的形状。

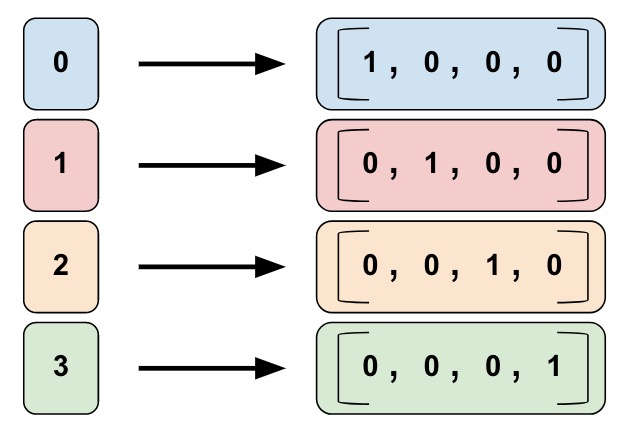
这里其实一个很大的弱点就是他能方便的表示“独立的单词”，但不能表示“上下文”，而上下文是机器理解文本的重要途经。相似和相近的词应该关系更加紧密，即空间上“位置更近”。

独热编码只用到n维中的一维，其他都是0，未免有些浪费。既然我们已经有n维空间了，那么是否能充分利用向量空间，在高维空间中也表示出彼此之间的距离呢？

2、word embedding

one-hot的表示方法是离散表示，我们要重点关注的word2vec是分布式连续表示。

Harris 在 1954 年提出的分布假说（ distributional hypothesis）：上下文相似的词，其语义也相似。

设有m个单词的单词表，嵌入的向量维度是n。（m>>n）

1、很多个单词共同在一个向量空间内，所以他们彼此一定不是线性无关的（否则就是独热编码，张成n维空间了），一定线性相关。

2、整个单词表一定不满秩，r(a1...am) <= n << m

3、每一维的数都有自己的意义，也可以计算欧式距离来表示两个词之间的含义是否相近。

比如：

我们有一个词汇表 m = 50,000 个单词，我们选择用 n = 300 维的向量来表示每个单词。

训练完成后，你会得到一个 50,000 x 300 的矩阵。这个矩阵的每一行就是一个单词的向量表示。这里的每一个数都是有意义的。\

（哈哈哈哈哈dbq我用画板写了很丑的例子哈哈哈哈哈哈哈哈）

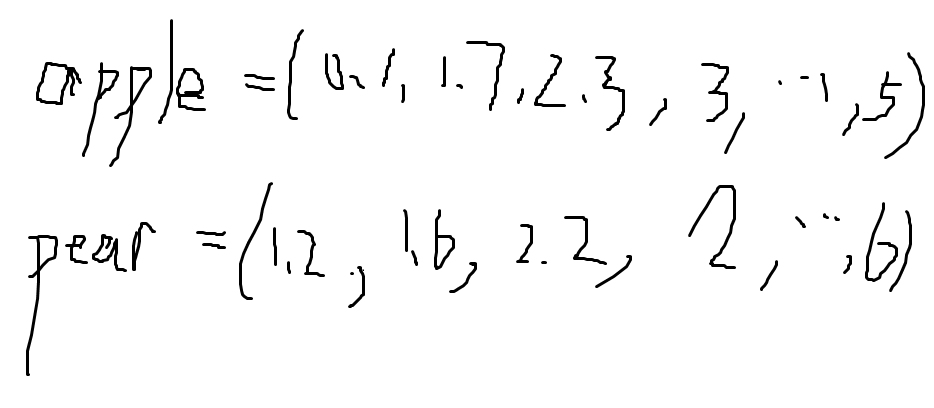
我们使用的是现成训练好的词汇表，如：​​Google、Stanford、Facebook 的预训练词向量​。已经基于海量预料训练好了。​​我们并不关心这个神经网络的预测结果，我们只关心它的副产物——网络权重，这些权重就是我们想要的词向量。​

然后进一步的话就是佬的文章里提到两种模型（训练方法）：

word embedding 精要整理 - Christbao - 博客园

Word2Vec模型中，主要有Skip-Gram和CBOW两种模型，从直观上理解，Skip-Gram是给定input word来预测上下文。​

3、ELMo

想象一下文章中有多义词的情况，一个单词有多个意思，也就是说基于多种上下文可能有多种含义，这时候单一的word2vec可能会导致歧义。

--------------2025/9/1 写累了歇一下（）

然后就在ELMo一文中解决了这个问题，很像动态word2vec，他可以基于不同上下文改变原有的word embedding。

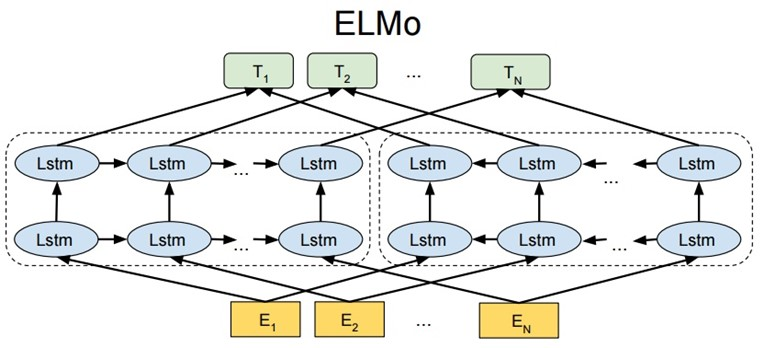
这里的输入是word embedding（图中的E），之后进入双向LSTM网络，最小化loss损失，更新向量。（这里我写的不一定准确哈，可以借鉴其他详细的文章~~）

【NLP-13】ELMo模型（Embeddings from Language Models） - 忆凡人生 - 博客园

最后，我觉得这个改进思想可以借鉴，把静态的模型改成静态，可以switch A to B，也可以change A。看到chain-of-thought论文中对long CoT进行优化时就有很多方法都是从这两个角度入手的，突然联想到，所以记录一下。

第一次写NLP相关的文章~希望大家有建议多多提出！加油加油！

再次感谢佬的文章，有所借鉴：

Word Embedding教程 - 李理的博客（but公式太严谨我没看下去TT）

word embedding 精要整理 - Christbao - 博客园

【NLP-13】ELMo模型（Embeddings from Language Models） - 忆凡人生 - 博客园