当前位置：首页 > news >正文

OpenGL视图变换矩阵详解：从理论推导到实战应用

news 2025/9/4 6:55:01

1 OpenGL坐标系系统

OpenGL使用右手坐标系作为其标准坐标系系统。在右手坐标系中，当您伸出右手，让拇指指向X轴正方向，食指指向Y轴正方向时，中指自然弯曲会指向Z轴正方向。这意味着在默认情况下，OpenGL中的正Z轴是朝向观察者之外的，而负Z轴则指向屏幕内部。

在图形渲染管线中，顶点需要经历一系列坐标系变换才能最终呈现在屏幕上。理解这些坐标系及其转换关系对于掌握OpenGL渲染机制至关重要：

模型坐标系 (Local Space)：也称为局部坐标系或对象坐标系，这是每个模型自有的坐标系系统，其原点通常位于模型的中心或某个预定义的点上。在模型坐标系中，所有顶点位置都是相对于模型自身原点定义的，这简化了模型的构建和初始变换。
世界坐标系 (World Space)：这是一个全局的、统一的坐标系系统，用于将所有模型放置在同一个场景空间中。世界坐标系定义了场景中所有物体（包括相机和光源）的绝对位置和方向。模型变换矩阵负责将顶点从模型坐标系转换到世界坐标系，这个过程通常包括平移、旋转和缩放操作。
视图坐标系 (View Space)：也称为观察空间或相机空间，这是一个以相机位置为原点、以相机朝向为方向的坐标系系统。视图变换矩阵负责将顶点从世界坐标系转换到视图坐标系，使得相机位于原点并朝向Z轴负方向。这个转换过程是本文的重点讨论内容。
裁剪坐标系 (Clip Space)：在这个坐标系中，顶点坐标被变换到一个标准化体积内（通常是一个单位立方体），位于这个体积之外的图元将被裁剪掉。投影变换矩阵负责将顶点从视图坐标系转换到裁剪坐标系，这个变换定义了视锥体和投影方式（透视或正交）。
屏幕坐标系 (Screen Space)：这是最终的2D坐标系系统，用于将3D场景投影到2D显示平面上。在这个坐标系中，X和Y坐标对应于屏幕上的像素位置，而Z坐标则用于深度测试和遮挡计算。

理解这些坐标系及其转换关系是掌握OpenGL渲染流程的基础。视图变换作为连接世界坐标系和视图坐标系的关键步骤，在渲染管线中扮演着至关重要的角色。

2 视图变换的原理与作用

视图变换是OpenGL渲染管线中的一个关键步骤，它负责将场景中的物体从世界坐标系转换到观察者坐标系（也称为相机坐标系）。这个过程本质上是在模拟3D世界中的相机或观察者的位置和朝向，从而确定从什么位置、什么角度来观看场景。

从物理意义上理解，视图变换可以看作是将相机放置在场景中的特定位置并指向特定方向的过程。但在OpenGL的实现中，实际上采用的是相对运动的原理：不是真正移动相机，而是将整个世界场景进行相反的变换，使得相机"看起来"好像位于原点并朝向特定方向。这就好比在摄影中，不是移动相机来拍摄不同角度的景物，而是保持相机固定不动而旋转整个场景，最终达到相同的视觉效果。

视图变换在渲染管线中发挥着几个关键作用：

确定观察视角：通过定义相机的位置和朝向，视图变换确定了观察场景的视角和方向。这使得我们可以从任意位置和角度观察3D场景，从而创造出丰富的视觉效果和动态体验。
建立视觉空间：视图变换建立了一个以相机为中心的坐标系系统，在这个系统中，相机的位置位于原点(0,0,0)，相机的朝向指向Z轴负方向。这个标准化视图空间简化了后续的投影和裁剪计算。
提供观察抽象：通过视图变换，开发者可以专注于场景的构建和物体的摆放，而不需要关心底层的观察机制。只需要通过简单的接口（如相机位置、目标点和上向量）即可控制观察条件。

在OpenGL渲染管线中，视图变换通常是在模型变换之后、投影变换之前应用的。这意味着我们先通过模型变换将物体放置在世界坐标系中的适当位置，然后通过视图变换将这些物体转换到相机坐标系，最后通过投影变换将3D场景投影到2D视平面上。

视图变换与模型变换经常被合并为一个模型-视图矩阵（Model-View Matrix），这个组合矩阵可以同时完成从模型坐标系到视图坐标系的转换。这种合并不仅减少了矩阵计算的数量，提高了渲染效率，还简化了着色器中的矩阵操作。

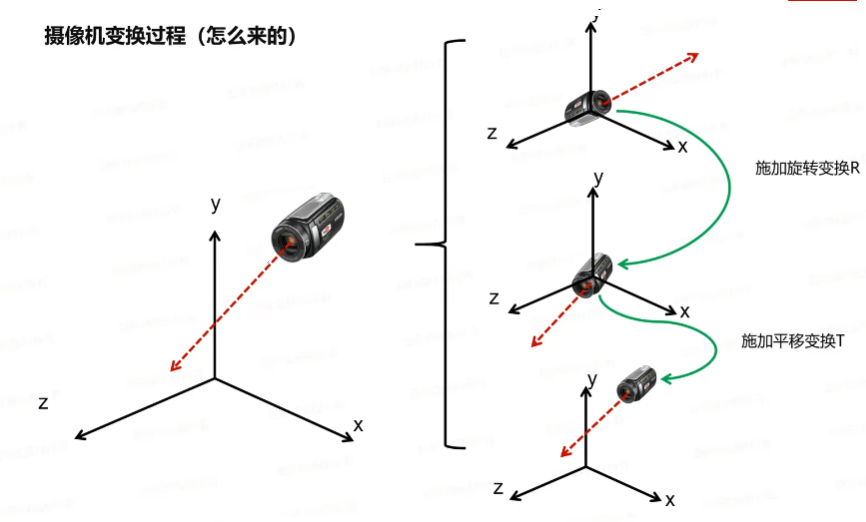
3 视图变换矩阵的数学推导

视图变换矩阵的推导是理解OpenGL视图变换的核心。我们将从相机参数的数学定义开始，逐步推导出完整的视图变换矩阵。

3.1 相机参数的数学定义

要定义相机在3D空间中的状态，我们需要三个基本参数：

eye：相机在世界坐标系中的位置，通常表示为点 $P=\left(p_{x}, p_{y}, p_{z}\right)$
center：相机看向的目标点位置，表示为点 $T=\left(t_{x}, t_{y}, t_{z}\right)$
up：相机的大致"向上"方向，通常表示为向量 $\bar{U}=\left(u_{x}, u_{y}, u_{z}\right)$

从这些基本参数，我们可以推导出描述相机朝向的三个相互垂直的基向量：

观察方向向量 (N)：这是相机朝向的反方向，由目标点减去相机位置得到：
注意：由于OpenGL是右手坐标系，相机默认看向Z轴负方向，所以这里使用P-T而不是T-P。
右向量 (U)：这是相机空间的X轴正方向，通过观察方向与上向量的叉积得到：
其中 $\vec{U}_{\text {approx }}$ 是用户提供的近似上向量。
上向量 (V)：这是相机空间的Y轴正方向，通过右向量与观察方向的叉积得到：
这个计算确保了三个向量相互垂直，即使用户提供的up向量不是完全垂直于观察方向。

3.2 视图变换矩阵的构造

视图变换需要两个基本步骤：平移和旋转。我们需要构造两个矩阵：一个平移矩阵T和一个旋转矩阵R。

3.2.1 平移矩阵

平移矩阵的目的是将相机从其在世界坐标系中的位置移动到世界坐标系的原点。如果相机位置是 $P=\left(p_{x}, p_{y}, p_{z}\right)$ ，那么平移矩阵为：

这个矩阵将任何点 $(x,y,z)$ 平移 $\left(-p_{x},-p_{y},-p_{z}\right)$ ，从而将相机移动到原点。

3.2.2 旋转矩阵

旋转矩阵的目的是将相机坐标系的方向向量对齐到世界坐标系的标准轴上。具体来说，我们需要将相机的右向量U对齐到世界坐标系的X轴(1,0,0)，上向量V对齐到Y轴(0,1,0)，观察方向N对齐到Z轴(0,0,1)。

由于旋转矩阵是正交矩阵，其逆矩阵等于其转置矩阵。因此，将世界坐标系旋转到相机坐标系的矩阵可以由相机坐标系的基向量组成：

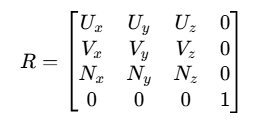
这个矩阵的逆矩阵（即转置矩阵）会将相机坐标系旋转到世界坐标系：

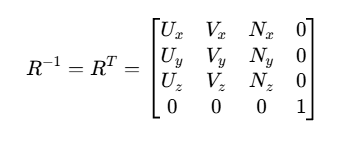
3.2.3 组合视图变换矩阵

完整的视图变换矩阵是先平移后旋转的组合。根据矩阵乘法的结合律，我们先应用平移变换，然后应用旋转变换：

将两个矩阵相乘，我们得到完整的视图变换矩阵：

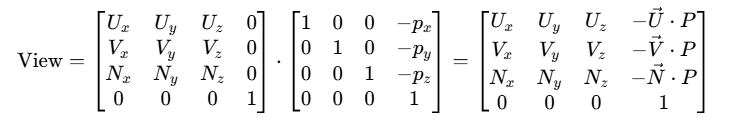
这个最终的视图变换矩阵可以将任何世界坐标系中的点转换到相机坐标系中。矩阵最右边一列的三个元素分别是相机位置向量与三个基向量的点积的负数，它们代表了相机原点在世界坐标系中相对于其自身坐标系各轴的位置经过平移和旋转后的综合补偿值。

4 GLM库LookAt函数解析

在实际的OpenGL编程中，我们通常不会手动计算视图变换矩阵，而是使用数学库提供的函数。GLM（OpenGL Mathematics）是一个广泛使用的C++数学库，专门为OpenGL设计，它提供了glm::lookAt函数来计算视图变换矩阵。

4.1 LookAt函数的基本实现

GLM库中的lookAt函数接受三个参数：相机位置（eye）、目标点（center）和上向量（up）。函数首先判断使用的是左手坐标系还是右手坐标系，然后调用相应的实现：

GLM_FUNC_QUALIFIER mat<4, 4, T, Q> lookAt(vec<3, T, Q> const& eye, vec<3, T, Q> const& center, vec<3, T, Q> const& up) 
{if(GLM_CONFIG_CLIP_CONTROL & GLM_CLIP_CONTROL_LH_BIT)return lookAtLH(eye, center, up);elsereturn lookAtRH(eye, center, up);
}

由于OpenGL默认使用右手坐标系，我们重点分析lookAtRH函数（RH代表Right-Handed）的实现。

4.2 lookAtRH函数的详细解析

GLM_FUNC_QUALIFIER mat<4, 4, T, Q> lookAtRH(vec<3, T, Q> const& eye, vec<3, T, Q> const& center, vec<3, T, Q> const& up) 
{// 计算观察方向向量（从eye指向center）vec<3, T, Q> const f(normalize(center - eye));// 计算右向量：观察方向与上向量的叉积vec<3, T, Q> const s(normalize(cross(f, up)));// 重新计算上向量：确保三个向量相互垂直vec<3, T, Q> const u(cross(s, f));// 初始化结果为4x4单位矩阵mat<4, 4, T, Q> Result(1);// 设置旋转部分Result[0][0] = s.x;  // 右向量的x分量Result[1][0] = s.y;  // 右向量的y分量Result[2][0] = s.z;  // 右向量的z分量Result[0][1] = u.x;  // 上向量的x分量Result[1][1] = u.y;  // 上向量的y分量Result[2][1] = u.z;  // 上向量的z分量Result[0][2] = -f.x; // 观察方向的负x分量（指向屏幕内）Result[1][2] = -f.y; // 观察方向的负y分量Result[2][2] = -f.z; // 观察方向的负z分量// 设置平移部分Result[3][0] = -dot(s, eye); // 右向量与eye的点积的负数Result[3][1] = -dot(u, eye); // 上向量与eye的点积的负数Result[3][2] = dot(f, eye);  // 观察方向与eye的点积return Result;
}

4.3 理论与实现的对应关系

将GLM的实现与我们之前的数学推导进行比较，可以发现它们完全一致：

f（forward）对应我们推导中的观察方向向量，但注意：f = normalize(center - eye)，而我们推导中的N = normalize(eye - center)，所以f = -N。
s（side）对应我们推导中的右向量U。
u（up）对应我们推导中的上向量V。

矩阵的构造也完全符合我们的推导结果：

前三行前三列是旋转部分，由三个基向量组成
最后一列的前三个元素是平移部分，是基向量与相机位置点积的负数

特别需要注意的是Result[3][2] = dot(f, eye)这一行。由于f = -N，所以这里实际上是dot(-N, eye) = -N·eye，与我们推导中的一致。

GLM的实现还处理了一些边界情况，比如确保up向量与观察方向不平行（否则叉积结果为零向量），以及所有向量都进行归一化处理以保证旋转矩阵的正交性。

5 视图变换在渲染管线中的应用

理解了视图变换矩阵的推导和实现后，我们需要了解它在OpenGL渲染管线中的具体应用方式。视图变换是渲染管线中模型-视图-投影（MVP）变换的重要组成部分。

5.1 渲染管线中的顶点变换

在OpenGL渲染管线中，每个顶点都需要经历一系列坐标变换才能最终显示在屏幕上。这些变换通常通过顶点着色器实现，主要包括以下步骤：

模型变换：将顶点从模型坐标系转换到世界坐标系
视图变换：将顶点从世界坐标系转换到视图坐标系
投影变换：将顶点从视图坐标系转换到裁剪坐标系

在现代的OpenGL编程中，这些变换通常在顶点着色器中通过矩阵乘法实现：

#version 330 corelayout(location = 0) in vec3 aPos;
uniform mat4 model;
uniform mat4 view;
uniform mat4 projection;void main()
{gl_Position = projection * view * model * vec4(aPos, 1.0);
}

需要注意的是，由于OpenGL矩阵是列主序（Column-Major）存储的，并且矩阵乘法是从右向左进行的，所以变换顺序是反向的：先应用的变换在右侧。

5.2 视图矩阵的传递和使用

在应用程序中，我们需要计算视图矩阵并将其传递给着色器程序。以下是一个典型的示例：

// 包含GLM头文件
#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>// 设置相机参数
glm::vec3 eye(0.0f, 0.0f, 3.0f);    // 相机位置
glm::vec3 center(0.0f, 0.0f, 0.0f); // 目标点
glm::vec3 up(0.0f, 1.0f, 0.0f);     // 上向量// 计算视图矩阵
glm::mat4 view = glm::lookAt(eye, center, up);// 获取着色器程序中uniform变量的位置
GLint viewLoc = glGetUniformLocation(shaderProgram, "view");// 将视图矩阵传递给着色器
glUniformMatrix4fv(viewLoc, 1, GL_FALSE, glm::value_ptr(view));

5.3 相机移动和旋转的实现

通过改变相机参数，我们可以实现相机的移动和旋转效果。例如，实现一个第一人称相机：

// 相机状态
glm::vec3 cameraPos(0.0f, 0.0f, 3.0f);
glm::vec3 cameraFront(0.0f, 0.0f, -1.0f);
glm::vec3 cameraUp(0.0f, 1.0f, 0.0f);// 处理键盘输入，移动相机
void processKeyboard(int key, float deltaTime)
{float cameraSpeed = 2.5f * deltaTime;if (key == GLFW_KEY_W)cameraPos += cameraSpeed * cameraFront;if (key == GLFW_KEY_S)cameraPos -= cameraSpeed * cameraFront;if (key == GLFW_KEY_A)cameraPos -= glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed;if (key == GLFW_KEY_D)cameraPos += glm::normalize(glm::cross(cameraFront, cameraUp)) * cameraSpeed;
}// 处理鼠标移动，旋转相机
void processMouseMovement(float xoffset, float yoffset)
{float sensitivity = 0.1f;xoffset *= sensitivity;yoffset *= sensitivity;yaw += xoffset;pitch += yoffset;// 防止相机翻转if (pitch > 89.0f)pitch = 89.0f;if (pitch < -89.0f)pitch = -89.0f;glm::vec3 front;front.x = cos(glm::radians(yaw)) * cos(glm::radians(pitch));front.y = sin(glm::radians(pitch));front.z = sin(glm::radians(yaw)) * cos(glm::radians(pitch));cameraFront = glm::normalize(front);
}// 在渲染循环中更新视图矩阵
glm::mat4 view = glm::lookAt(cameraPos, cameraPos + cameraFront, cameraUp);

这种实现方式允许用户通过键盘和鼠标控制相机，创造出沉浸式的3D体验。

5.4 性能优化考虑

在实时图形应用中，性能至关重要。以下是一些优化视图矩阵计算的建议：

避免重复计算：如果相机参数没有改变，不需要每一帧都重新计算视图矩阵。
预先计算MVP矩阵：在CPU端将模型、视图和投影矩阵相乘，然后一次性传递给着色器，减少GPU端的矩阵乘法操作。
使用逆矩阵：如果需要将点从视图空间转换回世界空间，可以计算视图矩阵的逆矩阵，而不是使用参数重新构造相机位置和方向。
利用矩阵特性：由于旋转矩阵是正交矩阵，其逆矩阵等于转置矩阵，这个特性可以用于简化一些计算。

通过合理优化，可以确保视图矩阵的计算不会成为渲染管线的性能瓶颈。

6 高级话题与优化

在掌握了视图变换的基本原理和应用后，我们可以进一步探讨一些高级话题和优化技术，这些内容将帮助您更深入地理解视图变换并在实际应用中实现更高效的效果。

6.1 视图矩阵的逆变换

有时我们需要将点从视图空间转换回世界空间，这就需要使用视图矩阵的逆矩阵。由于视图矩阵由平移和旋转组成，它的逆矩阵可以很容易地推导出来。

给定视图矩阵：

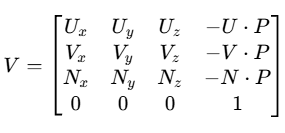
其逆矩阵为：

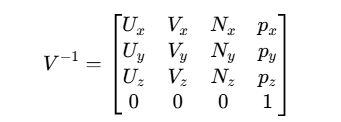
这个逆矩阵实际上就是相机坐标系到世界坐标系的变换矩阵，它将视图坐标系中的点转换回世界坐标系。

在GLM中，可以使用glm::inverse(viewMatrix)来计算逆矩阵，但了解其数学原理有助于优化计算，因为我们可以直接使用相机参数构造逆矩阵，而不需要进行通用的矩阵求逆运算。

6.2 视图矩阵与万向锁问题

当使用欧拉角表示相机朝向时，可能会遇到万向锁（Gimbal Lock）问题。万向锁发生在两个旋转轴对齐时，会导致失去一个旋转自由度。

为了避免万向锁问题，可以考虑以下解决方案：

使用四元数：四元数旋转表示法可以避免万向锁问题，并提供更平滑的插值。

// 使用四元数表示相机旋转
glm::quat cameraOrientation = glm::quat(glm::vec3(pitch, yaw, 0.0f));// 将四元数转换为视图矩阵
glm::mat4 view = glm::mat4_cast(cameraOrientation);
view = glm::translate(view, -cameraPos);

直接使用视图矩阵：通过构建视图矩阵而不是组合欧拉角旋转，可以避免万向锁问题。
限制旋转角度：避免使用会导致轴对齐的极端旋转角度。

6.3 视图裁减与视锥体剔除

视图变换与视锥体剔除密切相关。视锥体是场景中可见的空间区域，通常是一个平头锥体（透视投影）或长方体（正交投影）。视图变换将世界坐标系中的点转换到视图坐标系，使得后续的视锥体裁剪更加高效。

在视图坐标系中，视锥体的定义变得简单：

对于透视投影：视锥体是由近裁剪面、远裁剪面和四个侧面包围的区域
对于正交投影：视锥体是一个轴对齐的盒子

可以在视图坐标系中执行视锥体剔除，提前丢弃不可见的物体，提高渲染性能。

6.4 多视图设置与立体渲染

在高级图形应用中，如虚拟现实和立体显示，可能需要同时处理多个视图。例如，立体渲染需要为左眼和右眼分别计算视图矩阵。

// 立体渲染：左眼和右眼视图
glm::mat4 leftView = glm::lookAt(leftEyePos, center, up);
glm::mat4 rightView = glm::lookAt(rightEyePos, center, up);// 为每只眼设置不同的投影矩阵（通常有轻微偏移）
glm::mat4 leftProjection = glm::perspective(fov, aspect, near, far);
glm::mat4 rightProjection = glm::perspective(fov, aspect, near, far);