[信号与系统个人笔记]第三章 连续时间信号与系统的频域分析 Part 2
Update
- 2025.8.31
- 3.1 连续时间周期信号的傅里叶级数
- 2025.9.1
- 3.2 连续时间周期信号的频谱分析
- 2025.9.2
- 3.3 连续时间信号的傅里叶变换 part1
- 2025.9.3
- 3.3 连续时间信号的傅里叶变换 part2
3.3 连续时间信号的傅里叶变换
傅里叶变换的定义
频谱密度的引入
- 对于周期信号而言,信号周期TTT越大,频谱谱线越密集,幅度减小
- 信号周期TTT无限大时,周期信号变为非周期信号,谱线无限密集,幅度无穷小,离散谱过度为连续谱,需要改用密度描述频谱特性
傅里叶正变换
已知:
Fn=1T∫−T2T2f(t)e−jnΩtdt
F_{n}=\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)e^{-jn\Omega t}dt
Fn=T1∫−2T2Tf(t)e−jnΩtdt
当T→∞T\to \inftyT→∞:
- Ω→dω\Omega\to d\omegaΩ→dω,频谱间隔无限密集,变为无穷小量
- nΩ→ωn\Omega\to \omeganΩ→ω,离散频率→\to→连续频率
频谱密度:单位频率的信号频谱值
F(jω)=limT→∞Fnf=limT→∞∫−T2T2f(t)e−jnΩtdt=∫−∞+∞f(t)e−jωtdt
F(j\omega)=\lim_{ T \to \infty } \frac{F_{n}}{f} =\lim_{ T \to \infty } \int_{-\frac{T}{2}}^{\frac{T}{2}}f(t)e^{-jn\Omega t}dt=\int_{-\infty}^{+\infty}f(t)e^{-j\omega t}dt
F(jω)=T→∞limfFn=T→∞lim∫−2T2Tf(t)e−jnΩtdt=∫−∞+∞f(t)e−jωtdt
傅里叶正变换:F(jω)=∫−∞+∞f(t)e−jωtdt
傅里叶正变换:F(j\omega)=\int_{-\infty}^{+\infty}f(t)e^{-j\omega t}dt
傅里叶正变换:F(jω)=∫−∞+∞f(t)e−jωtdt
傅里叶反变换
已知:
f(t)=∑n=−∞∞FnejnΩt=1T∑n=−∞∞FnTejnΩt
f(t)=\sum_{n=-\infty}^{\infty}F_{n}e^{jn\Omega t}=\frac{1}{T}\sum_{n=-\infty}^{\infty}F_{n}Te^{jn\Omega t}
f(t)=n=−∞∑∞FnejnΩt=T1n=−∞∑∞FnTejnΩt
当T→∞T\to \inftyT→∞时:
- Ω→dω\Omega\to d\omegaΩ→dω,频谱间隔无限密集,变为无穷小量
- nΩ→ωn\Omega\to \omeganΩ→ω,离散频率→\to→连续频率
- limT→∞FnT=F(jω)\lim_{ T \to \infty }F_{n}T=F(j\omega)limT→∞FnT=F(jω)
- 1T=Ω2π→dω2π\frac{1}{T}=\frac{\Omega}{2\pi}\to \frac{d\omega}{2\pi}T1=2πΩ→2πdω
则:
傅里叶反变换:f(t)=12π∫−∞+∞F(jω)ejωtdω 傅里叶反变换:f(t)=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(j\omega)e^{j\omega t}d\omega 傅里叶反变换:f(t)=2π1∫−∞+∞F(jω)ejωtdω
傅里叶变换对
f(t)↔F(jω)
f(t) \leftrightarrow F(j\omega)
f(t)↔F(jω)
傅里叶正变换:F(jω)=F[f(t)]傅里叶反变换:f(t)=F−1[F(jω)]
\begin{align}
&傅里叶正变换:F(j\omega)=\mathcal{F}[f(t)]\\ \\
&傅里叶反变换: f(t)=\mathcal{F}^{-1}[F(j\omega)]
\end{align}
傅里叶正变换:F(jω)=F[f(t)]傅里叶反变换:f(t)=F−1[F(jω)]
傅里叶变换存在的充分条件
信号满足绝对可积条件:∫−∞+∞∣f(t)∣dt<∞ ⟹ 傅里叶变换存在 信号满足绝对可积条件:\int_{-\infty}^{+\infty}|f(t)|dt<\infty \implies傅里叶变换存在 信号满足绝对可积条件:∫−∞+∞∣f(t)∣dt<∞⟹傅里叶变换存在
- 注意此处为充分条件,傅里叶变换存在不一定信号绝对可积
- 阶跃信号ε(t)\varepsilon(t)ε(t)的广义傅里叶变换存在,但不满足绝对可积
常用结论
F(0)=F(jω)∣ω=0=∫−∞+∞f(t)dtf(0)=f(t)∣ω=0=12π∫−∞+∞F(jω)dω \begin{align} &F(0)=F(j\omega)\bigg|_{\omega=0}=\int_{-\infty}^{+\infty}f(t)dt\\ \\ &f(0)=f(t)\bigg|_{\omega=0}=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(j\omega )d\omega \end{align} F(0)=F(jω)ω=0=∫−∞+∞f(t)dtf(0)=f(t)ω=0=2π1∫−∞+∞F(jω)dω
频谱密度函数
信号为实函数:
F(jω)=∫−∞+∞f(t)e−jωtdt=∫−∞+∞f(t)cosωtdt−j∫−∞+∞f(t)sinωtdt=R(ω)+jX(ω)
\begin{align}
F(j\omega)&=\int_{-\infty}^{+\infty}f(t)e^{-j\omega t}dt=\int_{-\infty}^{+\infty}f(t)\cos \omega tdt-j\int_{-\infty}^{+\infty}f(t)\sin \omega tdt\\ \\
&=R(\omega)+jX(\omega)
\end{align}
F(jω)=∫−∞+∞f(t)e−jωtdt=∫−∞+∞f(t)cosωtdt−j∫−∞+∞f(t)sinωtdt=R(ω)+jX(ω)
- 频谱为复函数,含有实部和虚部
{R(ω)=∫−∞+∞f(t)cosωtdtR(−ω)=R(ω)为ω的偶函数X(ω)=−∫−∞+∞f(t)sinωtdtX(−ω)=−X(ω)为ω的奇函数
\begin{cases}
R(\omega)=\int_{-\infty}^{+\infty}f(t)\cos \omega tdt\quad R(-\omega)=R(\omega)\quad 为\omega的偶函数\\ \\
X(\omega)=-\int_{-\infty}^{+\infty}f(t)\sin \omega tdt\quad X(-\omega)=-X(\omega)\quad 为\omega的奇函数
\end{cases}
⎩⎨⎧R(ω)=∫−∞+∞f(t)cosωtdtR(−ω)=R(ω)为ω的偶函数X(ω)=−∫−∞+∞f(t)sinωtdtX(−ω)=−X(ω)为ω的奇函数
F(jω)=∣F(jω)∣ejφ(ω)
F(j\omega)=|F(j\omega)|e^{j\varphi(\omega)}
F(jω)=∣F(jω)∣ejφ(ω)
其中:
∣F(jω)∣=R2(ω)+X2(ω)∣F(−ω)∣=∣F(ω)∣为ω的偶函数,具有幅频特性φ(ω)=arctanX(ω)R(ω)φ(−ω)=−φ(ω)为ω的奇函数,具有相频特性
\begin{align}
&|F(j\omega)|=\sqrt{ R^{2}(\omega)+X^{2}(\omega) }\quad |F(-\omega)|=|F(\omega)|\quad 为\omega 的偶函数,具有幅频特性\\ \\
&\varphi(\omega)=\arctan \frac{X(\omega)}{R(\omega)}\quad \varphi(-\omega)=-\varphi(\omega)\quad 为\omega的奇函数,具有相频特性
\end{align}
∣F(jω)∣=R2(ω)+X2(ω)∣F(−ω)∣=∣F(ω)∣为ω的偶函数,具有幅频特性φ(ω)=arctanR(ω)X(ω)φ(−ω)=−φ(ω)为ω的奇函数,具有相频特性
常见信号的傅里叶变换
矩形脉冲(门函数)
gτ(t)=[ε(t+τ2)−ε(t−τ2)]={1∣t∣≤τ20∣t∣>τ2 g_{\tau}(t)=\left[ \varepsilon\left( t+ \frac{\tau}{2} \right) -\varepsilon\left( t- \frac{\tau}{2} \right)\right]=\begin{cases} 1\quad|t|\leq \frac{\tau}{2}\\ \\ 0\quad |t|> \frac{\tau}{2} \end{cases} gτ(t)=[ε(t+2τ)−ε(t−2τ)]=⎩⎨⎧1∣t∣≤2τ0∣t∣>2τ
门函数傅里叶变换推导:
F(jω)=∫−∞+∞f(t)e−jωtdt=∫−τ2τ2e−jωtdt=1−jωe−jωt∣−τ2τ2=2(ejωτ2−e−jωτ2)2jω=2ωsinωτ2=2ω⋅sinωτ2ωτ2⋅ωτ2=τSa(ωτ2)
\begin{align}
F(j\omega)&=\int_{-\infty}^{+\infty}f(t)e^{-j\omega t}dt=\int_{-\frac{\tau}{2}}^{ \frac{\tau}{2}}e^{-j\omega t}dt=\frac{1}{-j\omega}e^{-j\omega t}\bigg|_{-\frac{\tau}{2}}^{\frac{\tau}{2}}\\ \\
&= \frac{2\left( e^{j\omega \frac{\tau}{2}}-e^{-j\omega \frac{\tau}{2}} \right)}{2j\omega}=\frac{2}{\omega}\sin \frac{\omega \tau}{2}\\ \\
&=\frac{2}{\omega}\cdot \frac{\sin \frac{\omega \tau}{2}}{ \frac{\omega \tau}{2}}\cdot \frac{\omega \tau}{2}=\tau Sa\left( \frac{\omega \tau}{2} \right)
\end{align}
F(jω)=∫−∞+∞f(t)e−jωtdt=∫−2τ2τe−jωtdt=−jω1e−jωt−2τ2τ=2jω2(ejω2τ−e−jω2τ)=ω2sin2ωτ=ω2⋅2ωτsin2ωτ⋅2ωτ=τSa(2ωτ)
结论:
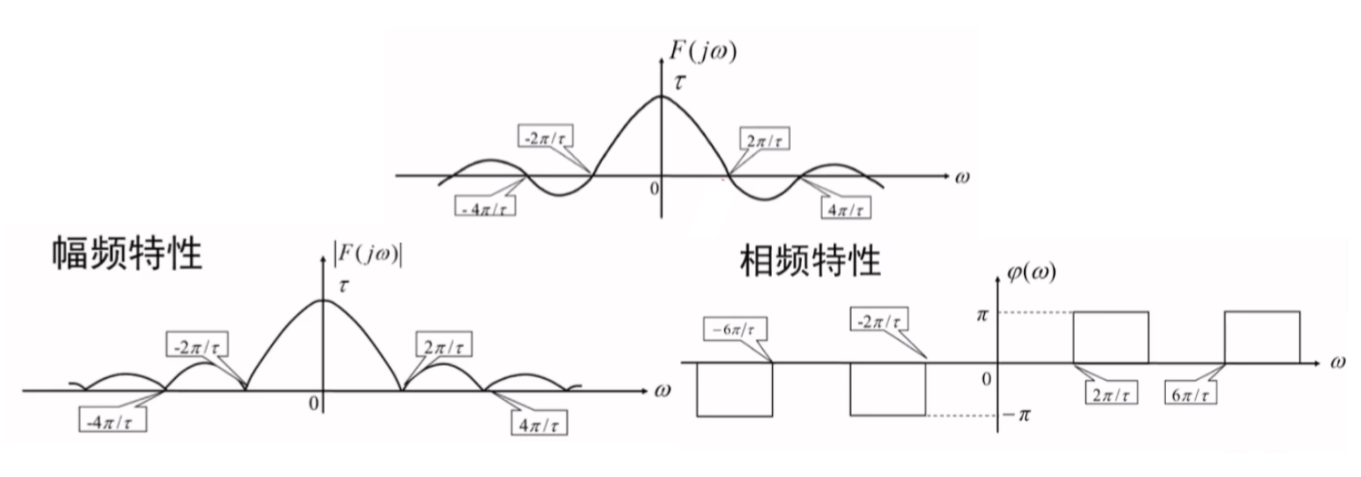
gτ(t)↔τSa(ωτ2)
g_{\tau}(t)\leftrightarrow \tau Sa\left( \frac{\omega \tau}{2} \right)
gτ(t)↔τSa(2ωτ)
-
该频谱为实频谱,实频谱的幅度、相位合二为一
-
有效带宽通过第一过零点可知Bω=2πτ(rad/s)B_{\omega}= \frac{2\pi}{\tau}(rad/s)Bω=τ2π(rad/s)
-
由于频谱为实频谱,幅频特性只需要取绝对值即可
-
由于频谱为实频谱,相频特性只会出现−π,0,π-\pi,0,\pi−π,0,π,分别对应cosθ={−1,1}\cos \theta=\{ -1,1 \}cosθ={−1,1},即频谱密度为正时相频为000,频谱密度为负时相频为π\piπ,负半轴通过原点对称可得π→−π\pi\to-\piπ→−π
特殊结论:
时域有限的信号,频域上无限展宽
不知道啥意思
单边指数信号
f(t)=eαtε(t)={e−αtt≥00t<0(α>0)
f(t)=e^{\alpha t}\varepsilon(t)=\begin{cases}
e^{-\alpha t}\quad t\geq 0\\ \\
0\quad t< 0
\end{cases}(\alpha>0)
f(t)=eαtε(t)=⎩⎨⎧e−αtt≥00t<0(α>0)
单边指数函数傅里叶变换推导:
F(jω)=∫0+∞e−αt⋅e−jωtdt=∫0+∞e−(α+jω)tdt=1−(α+jω)e−(α+jω)t∣0+∞=1α+jω
\begin{align}
F(j\omega)&=\int_{0}^{+\infty}e^{-\alpha t}\cdot e^{-j\omega t}dt=\int_{0}^{+\infty}e^{-(\alpha+j\omega)t}dt\\ \\
&=\frac{1}{-(\alpha+j\omega)}e^{-(\alpha+j\omega)t}\bigg|_{0}^{+\infty}=\frac{1}{\alpha+j\omega}
\end{align}
F(jω)=∫0+∞e−αt⋅e−jωtdt=∫0+∞e−(α+jω)tdt=−(α+jω)1e−(α+jω)t0+∞=α+jω1
结论:
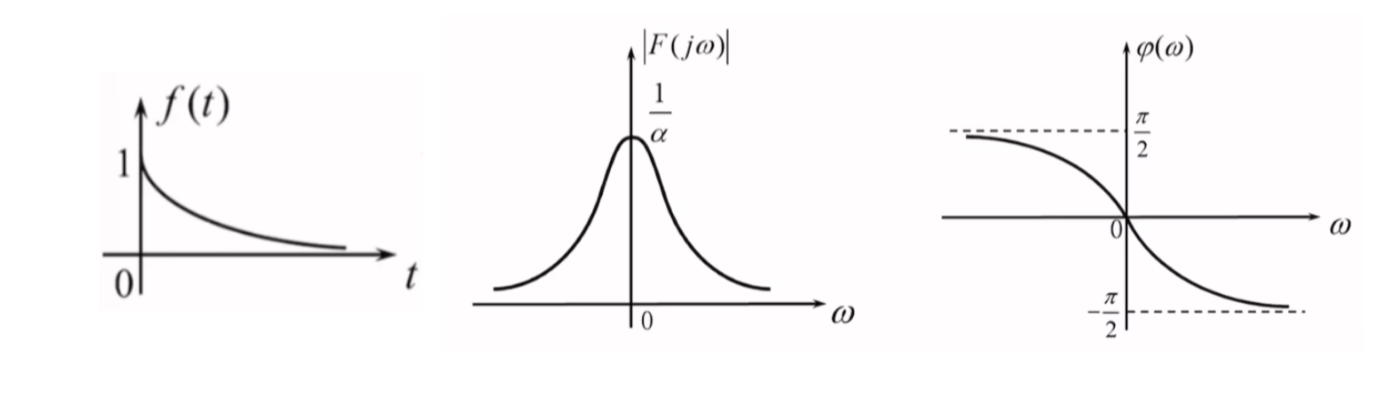
eαtε(t)↔1α+jω
e^{\alpha t}\varepsilon(t)\leftrightarrow \frac{1}{\alpha+j\omega}
eαtε(t)↔α+jω1
幅频特性:
∣F(jω)∣=∣1α+jω∣=1∣α+jω∣=1α2+ω2
|F(j\omega)|=\left| \frac{1}{\alpha+j\omega} \right|=\frac{1}{|\alpha+j\omega|}=\frac{1}{\sqrt{ \alpha^{2}+\omega^{2} }}
∣F(jω)∣=α+jω1=∣α+jω∣1=α2+ω21
相频特性:
φ(ω)=∠1α+jω=∠1−∠(α+jω)=0°−arctanωα=−arctanωα
\varphi(\omega)=\angle \frac{1}{\alpha+j\omega}=\angle 1-\angle(\alpha+j\omega)=0{\degree}-\arctan \frac{\omega}{\alpha}=-\arctan \frac{\omega}{\alpha}
φ(ω)=∠α+jω1=∠1−∠(α+jω)=0°−arctanαω=−arctanαω
偶双边指数信号
f(t)=e−α∣t∣={e−αtt>0eαtt<0(α>0)
f(t)=e^{-\alpha |t|}=\begin{cases}
e^{-\alpha t}\quad t>0\\ \\
e^{\alpha t}\quad t<0
\end{cases}\quad(\alpha>0)
f(t)=e−α∣t∣=⎩⎨⎧e−αtt>0eαtt<0(α>0)
偶双边指数函数傅里叶变换推导:
F(jω)=∫−∞0eαt⋅e−jωtdt+∫0+∞e−αt⋅e−jωtdt=∫−∞0e(α−jω)tdt+∫0+∞e−(α+jω)tdt=1α−jωe(α−jω)t∣−∞0+1−(α+jω)e−(α+jω)t∣0+∞=1α−jω+1α+jω=2αα2+ω2
\begin{align}
F(j\omega)&=\int_{-\infty}^{0}e^{\alpha t}\cdot e^{-j\omega t}dt+\int_{0}^{+\infty}e^{-\alpha t}\cdot e^{-j\omega t}dt\\ \\
&=\int_{-\infty}^{0}e^{(\alpha-j\omega )t}dt+\int_{0}^{+\infty}e^{-(\alpha+j\omega)t}dt\\ \\
&=\frac{1}{\alpha-j\omega}e^{(\alpha-j\omega)t}\bigg|_{-\infty}^{0}+ \frac{1}{-(\alpha+j\omega )}e^{-(\alpha+j\omega)t}\bigg|_{0}^{+\infty}\\ \\
&=\frac{1}{\alpha-j\omega}+\frac{1}{\alpha+j\omega}= \frac{2\alpha}{\alpha^{2}+\omega^{2}}
\end{align}
F(jω)=∫−∞0eαt⋅e−jωtdt+∫0+∞e−αt⋅e−jωtdt=∫−∞0e(α−jω)tdt+∫0+∞e−(α+jω)tdt=α−jω1e(α−jω)t−∞0+−(α+jω)1e−(α+jω)t0+∞=α−jω1+α+jω1=α2+ω22α
结论:
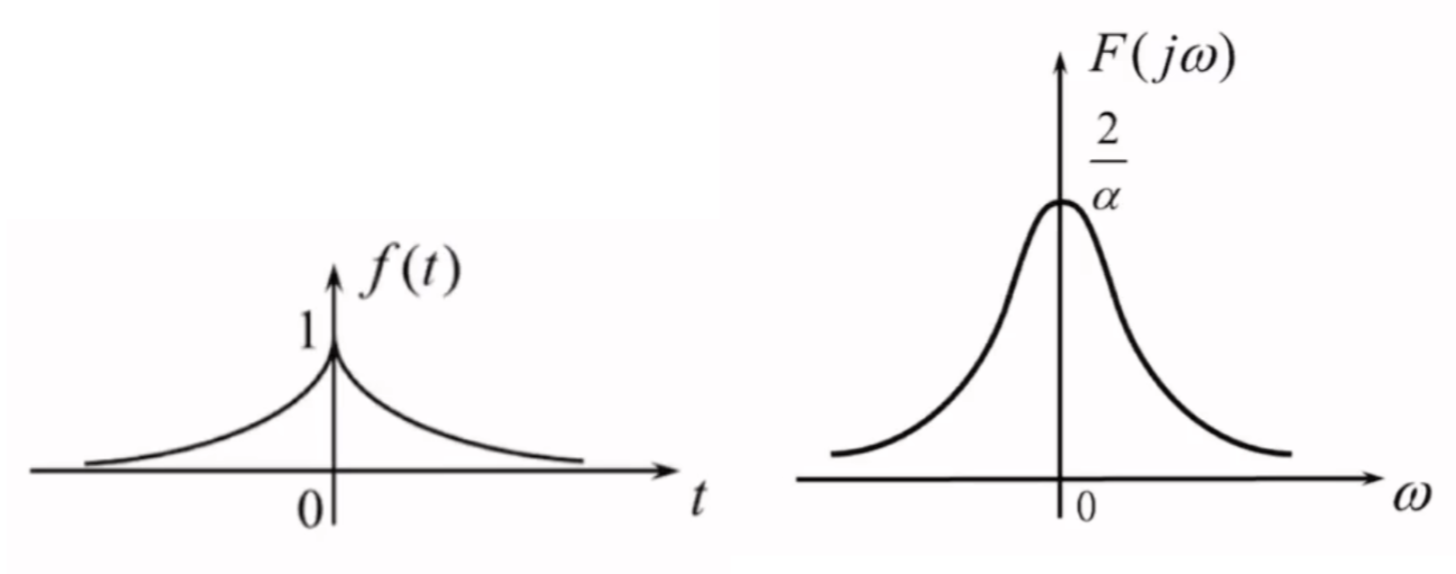
e−α∣t∣↔2αα2+ω2(α>0)
e^{-\alpha |t|}\leftrightarrow \frac{2\alpha}{\alpha^{2}+\omega^{2}}\quad (\alpha>0)
e−α∣t∣↔α2+ω22α(α>0)
幅频特性:
- 由于频谱为实频谱,幅频特性直接取绝对值
- ∣F(jω)∣=2αα2+ω2|F(j\omega)|= \frac{2\alpha}{\alpha^{2}+\omega^{2}}∣F(jω)∣=α2+ω22α
相频特性:
- 由于频谱为恒正的实频谱,相位恒为0
- φ(ω)=0\varphi(\omega)=0φ(ω)=0
奇双边指数信号
f(t)={e−αtt>0−eαtt<0(α>0)
f(t)=\begin{cases}
e^{-\alpha t}\quad t>0\\ \\
-e^{\alpha t }\quad t< 0
\end{cases}\quad (\alpha>0)
f(t)=⎩⎨⎧e−αtt>0−eαtt<0(α>0)
奇双边指数函数傅里叶变换推导:
F(jω)=−∫−∞0eαt⋅e−jωtdt+∫0+∞e−αt⋅te−jωtdt=1α+jω−1α−jω=−j⋅2ωα2+ω2
\begin{align}
F(j\omega)&=-\int_{-\infty}^{0}e^{\alpha t}\cdot e^{-j\omega t}dt+\int_{0}^{+\infty}e^{-\alpha t}\cdot t e^{-j\omega t}dt\\ \\
&=\frac{1}{\alpha+j\omega}-\frac{1}{\alpha-j\omega}= \frac{-j \cdot2\omega}{\alpha^{2}+\omega^{2}}
\end{align}
F(jω)=−∫−∞0eαt⋅e−jωtdt+∫0+∞e−αt⋅te−jωtdt=α+jω1−α−jω1=α2+ω2−j⋅2ω
结论:
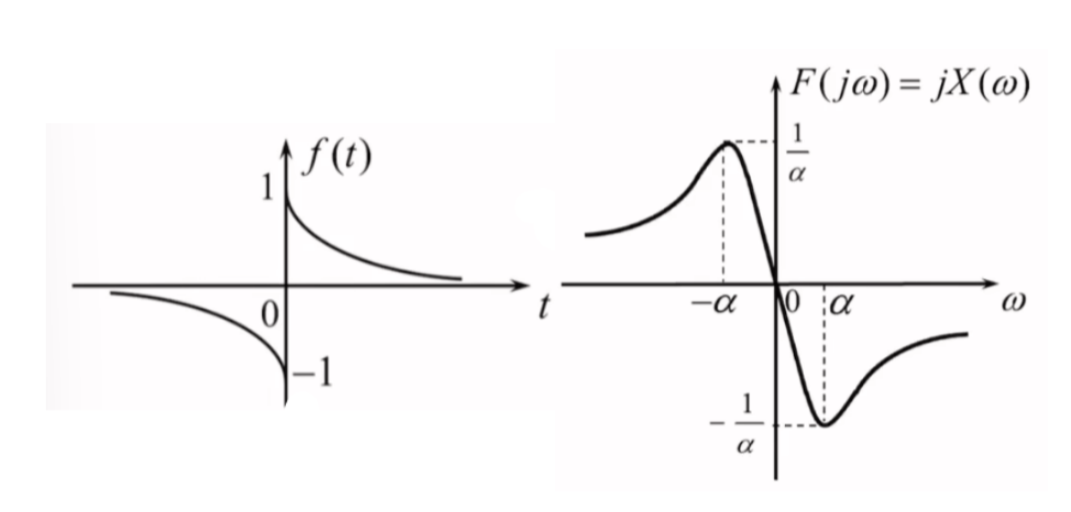
{e−αtt>0−eαtt<0↔−j⋅2ωα2+ω2(α>0)
\begin{cases}
e^{-\alpha t}\quad t>0\\ \\
-e^{\alpha t }\quad t< 0
\end{cases}
\leftrightarrow \frac{-j\cdot 2\omega}{\alpha^{2}+\omega^{2}}\quad (\alpha>0)
⎩⎨⎧e−αtt>0−eαtt<0↔α2+ω2−j⋅2ω(α>0)
幅频特性:
- 由于频谱为虚频谱,幅频特性即为频谱去掉虚数单位后取绝对值
- ∣F(jω)∣=2∣ω∣α2+ω2|F(j\omega)|= \frac{2|\omega|}{\alpha^{2}+\omega^{2}}∣F(jω)∣=α2+ω22∣ω∣
相频特性:
- 由于频谱为虚频谱,三角展开为jsinθj\sin \thetajsinθ,则相频取θ={−π2,π2}\theta=\left\{ -\frac{\pi}{2} ,\frac{\pi}{2} \right\}θ={−2π,2π}对应着频谱取{−j,j}\{ -j,j \}{−j,j}
φ(ω)={π2ω<0−π2ω>0 \varphi(\omega)=\begin{cases} \frac{\pi}{2}\quad \omega<0\\ \\ -\frac{\pi}{2}\quad \omega>0 \end{cases} φ(ω)=⎩⎨⎧2πω<0−2πω>0
冲激信号及其导数
*傅里叶变换的时域微分性质
设函数f(t)f(t)f(t)的傅里叶变换为F(ω)F(\omega)F(ω):
F{f(t)}=F(ω)=∫−∞+∞f(t)e−jωtdt
\mathcal{F}\{ f(t) \}=F(\omega)=\int_{-\infty}^{+\infty}f(t)e^{-j\omega t}dt
F{f(t)}=F(ω)=∫−∞+∞f(t)e−jωtdt
且f(t)f(t)f(t)及其各阶导数绝对可积,则有:
F{f(n)(t)}=(jω)nF(ω)
\mathcal{F}\{ f^{(n)}(t) \}=(j\omega)^{n}F(\omega)
F{f(n)(t)}=(jω)nF(ω)
推导关键在于:
- ∫−∞+∞f(t)dt<∞ ⟹ limt→∞f(t)=0\int_{-\infty}^{+\infty}f(t)dt<\infty\implies \lim_{ t \to \infty }f(t)=0∫−∞+∞f(t)dt<∞⟹limt→∞f(t)=0
- 对原积分采用分部积分,常数项为f(n−1)(t)e−jωt∣−∞+∞=0f^{(n-1)}(t)e^{-j\omega t}\bigg|_{-\infty}^{+\infty}=0f(n−1)(t)e−jωt−∞+∞=0
- 可以得到递推∫−∞+∞f(n)(t)e−jωtdt=(jω)∫−∞+∞f(n−1)(t)e−jωtdt\int_{-\infty}^{+\infty}f^{(n)}(t)e^{-j\omega t}dt=(j\omega )\int_{-\infty}^{+\infty}f^{(n-1)}(t)e^{-j\omega t}dt∫−∞+∞f(n)(t)e−jωtdt=(jω)∫−∞+∞f(n−1)(t)e−jωtdt
冲激信号傅里叶变换推导:
F(jω)=∫−∞+∞δ(t)e−jωtdt=e−jωt∣t=0=1即:δ(t)↔1
\begin{align}
F(j\omega)&=\int_{-\infty}^{+\infty }\delta(t)e^{-j\omega t}dt=e^{-j\omega t}\bigg|_{t=0}=1\\ \\
即:\quad&\delta(t)\leftrightarrow 1
\end{align}
F(jω)即:=∫−∞+∞δ(t)e−jωtdt=e−jωtt=0=1δ(t)↔1
由于F{f(n)(t)}=(jω)n∫−∞+∞f(t)e−jωtdt:F{δ(n)(t)}=(jω)n∫−∞+∞δ(t)e−jωtdt=(jω)n即:δ(n)(t)↔(jω)n
\begin{align}
&由于\mathcal{F}\{ f^{(n)}(t) \}=(j\omega)^{n}\int_{-\infty}^{+\infty}f(t)e^{-j\omega t}dt:\\ \\
&\mathcal{F}\{ \delta^{(n)}(t) \}=(j\omega)^{n}\int_{-\infty}^{+\infty}\delta(t)e^{-j\omega t}dt=(j\omega)^{n}\\ \\
&即:\quad \delta^{(n)}(t)\leftrightarrow (j\omega)^{n}
\end{align}
由于F{f(n)(t)}=(jω)n∫−∞+∞f(t)e−jωtdt:F{δ(n)(t)}=(jω)n∫−∞+∞δ(t)e−jωtdt=(jω)n即:δ(n)(t)↔(jω)n
直流信号f(t)=Af(t)=Af(t)=A
直流信号傅里叶变换推导过程:
F−1{δ(ω)}=12π∫−∞+∞δ(ω)ejωtdω=12πejωt∣ω=0=12π则:12π↔δ(ω) ⟹ 1↔2πδ(ω) ⟹ A↔2πAδ(ω)
\begin{align}
&\mathcal{F}^{-1}\{ \delta(\omega) \}=\frac{1}{2\pi}\int_{-\infty}^{+\infty}\delta(\omega)e^{j\omega t}d\omega=\frac{1}{2\pi}e^{j\omega t}\bigg|_{\omega=0}=\frac{1}{2\pi}\\ \\
&则: \frac{1}{2\pi}\leftrightarrow \delta(\omega)\implies 1\leftrightarrow 2\pi \delta(\omega)\implies A\leftrightarrow 2\pi A\delta(\omega)
\end{align}
F−1{δ(ω)}=2π1∫−∞+∞δ(ω)ejωtdω=2π1ejωtω=0=2π1则:2π1↔δ(ω)⟹1↔2πδ(ω)⟹A↔2πAδ(ω)
- 直流信号的傅里叶变换的推导过程借助了反傅里叶变换逆推而来
- 常数函数f(t)=Af(t)=Af(t)=A的傅里叶变换为2πAδ(ω)2\pi A\delta(\omega)2πAδ(ω),然而∫−∞+∞f(t)dt=∞\int_{-\infty}^{+\infty}f(t)dt=\infty∫−∞+∞f(t)dt=∞并不是绝对可积,这再次印证绝对可积是傅里叶变换的充分条件
- 冲激信号和常数的时、频特性存在对称性
- 冲激信号的傅里叶变换为常数δ(t)↔1\delta(t)\leftrightarrow 1δ(t)↔1
- 常数的傅里叶变换为冲激信号1↔2πδ(ω)1\leftrightarrow 2\pi\delta(\omega)1↔2πδ(ω)
符号函数
sgn(t)={−1t<01t>0
sgn(t)=\begin{cases}
-1\quad t<0\\ \\
1\quad t>0
\end{cases}
sgn(t)=⎩⎨⎧−1t<01t>0
符号函数傅里叶变换推导过程:
设fα(t)={e−αtt>0−eαtt<0(α>0)则fα(t)↔−j⋅2ωα2+ω2(α>0)而sgn(t)=limα→0fα(t)则sgn(t)↔广义傅里叶变换limα→0−j⋅2ωα2+ω2=2jω
\begin{align}
&设f_{\alpha}(t)=\begin{cases}
e^{-\alpha t}\quad t>0\\ \\
-e^{\alpha t}\quad t<0
\end{cases}\quad (\alpha>0)\\ \\
&则f_{\alpha}(t)\leftrightarrow \frac{-j\cdot 2\omega}{\alpha^{2}+\omega^{2}}\quad (\alpha>0)\\ \\
&而sgn(t)=\lim_{ \alpha \to 0 }f_{\alpha}(t) \\ \\
&则sgn(t)\xleftrightarrow{广义傅里叶变换}\lim_{ \alpha \to 0 } \frac{-j\cdot 2\omega}{\alpha^{2}+\omega^{2}}=\frac{2}{j\omega}
\end{align}
设fα(t)=⎩⎨⎧e−αtt>0−eαtt<0(α>0)则fα(t)↔α2+ω2−j⋅2ω(α>0)而sgn(t)=α→0limfα(t)则sgn(t)广义傅里叶变换α→0limα2+ω2−j⋅2ω=jω2
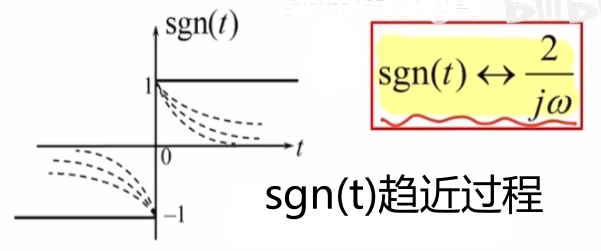
推导关键:
- 利用了奇双边指数信号在α→0\alpha\to 0α→0时趋近于sgn(t)sgn(t)sgn(t)的特性进行推导
- sgn(t)↔2jωsgn(t)\leftrightarrow \frac{2}{j\omega}sgn(t)↔jω2在广义傅里叶变换下成立
阶跃函数
ε(t)={1t>00t<0
\varepsilon(t)=\begin{cases}
1\quad t>0\\ \\
0\quad t<0
\end{cases}
ε(t)=⎩⎨⎧1t>00t<0
阶跃函数傅里叶变换推导过程:
由ε(t)=12+12sgn(t):ε(t)↔广义傅里叶变换πδ(ω)+1jω
\begin{align}
&由\varepsilon(t)=\frac{1}{2}+\frac{1}{2}sgn(t):\\ \\
&\varepsilon(t)\xleftrightarrow{广义傅里叶变换}\pi \delta(\omega)+ \frac{1}{j\omega}
\end{align}
由ε(t)=21+21sgn(t):ε(t)广义傅里叶变换πδ(ω)+jω1
- 利用ε(t)\varepsilon(t)ε(t)与符号函数的关系从而得到傅里叶变换
总结
傅里叶正变换:F(jω)=F{f(t)}=∫−∞+∞f(t)e−jωtdt傅里叶反变换:f(t)=F−1{F(jω)}=12π∫−∞+∞F(jω)ejωtdω时域t⇌傅里叶反变换傅里叶正变换频域ω
\begin{align}
&傅里叶正变换:F(j\omega)=\mathcal{F}\{ f(t) \}=\int_{-\infty}^{+\infty}f(t)e^{-j\omega t}dt\\ \\
&傅里叶反变换:f(t)=\mathcal{F}^{-1}\{ F(j\omega) \}=\frac{1}{2\pi}\int_{-\infty}^{+\infty}F(j\omega)e^{j\omega t}d\omega\\ \\
& 时域t\xrightleftharpoons[\text{傅里叶反变换}]{\text{傅里叶正变换}}频域\omega
\end{align}
傅里叶正变换:F(jω)=F{f(t)}=∫−∞+∞f(t)e−jωtdt傅里叶反变换:f(t)=F−1{F(jω)}=2π1∫−∞+∞F(jω)ejωtdω时域t傅里叶正变换傅里叶反变换频域ω
门函数:gτ(t)↔τSa(ωτ2)单边指数信号:e−αtε(t)↔1α+jω(α>0)偶双边指数信号:e−α∣t∣↔2αα2+ω2(α>0)奇双边指数信号:{e−αtt>0−eαtt<0↔−j⋅2ωα2+ω2(α>0)冲激信号及其导数:{δ(t)↔1δ(n)(t)↔(jω)n直流信号:1↔2πδ(ω)符号函数:sgn(t)↔2jω阶跃函数:ε(t)=12+12sgn(n)↔πδ(ω)+1jω
\begin{align}
&门函数:g_{\tau}(t)\leftrightarrow \tau Sa\left( \frac{\omega \tau}{2} \right)\\ \\
&单边指数信号:e^{-\alpha t}\varepsilon(t)\leftrightarrow \frac{1}{\alpha+j\omega}\quad (\alpha>0)\\ \\
&偶双边指数信号:e^{-\alpha |t|}\leftrightarrow \frac{2\alpha}{\alpha^{2}+\omega^{2}}\quad (\alpha>0)\\ \\
&奇双边指数信号:\begin{cases}
e^{-\alpha t}\quad t>0\\ \\
-e^{\alpha t}\quad t<0
\end{cases}\leftrightarrow \frac{-j\cdot 2\omega}{\alpha^{2}+\omega^{2}}\quad (\alpha>0)\\ \\
&冲激信号及其导数: \begin{cases}
\delta(t)\leftrightarrow 1\\ \\
\delta^{(n)}(t)\leftrightarrow (j\omega)^{n}
\end{cases}\\ \\
&直流信号:1\leftrightarrow 2\pi \delta(\omega)\\ \\
&符号函数:sgn(t)\leftrightarrow \frac{2}{j\omega}\\ \\
&阶跃函数: \varepsilon(t)=\frac{1}{2}+\frac{1}{2}sgn(n)\leftrightarrow \pi \delta(\omega)+ \frac{1}{j\omega}
\end{align}
门函数:gτ(t)↔τSa(2ωτ)单边指数信号:e−αtε(t)↔α+jω1(α>0)偶双边指数信号:e−α∣t∣↔α2+ω22α(α>0)奇双边指数信号:⎩⎨⎧e−αtt>0−eαtt<0↔α2+ω2−j⋅2ω(α>0)冲激信号及其导数:⎩⎨⎧δ(t)↔1δ(n)(t)↔(jω)n直流信号:1↔2πδ(ω)符号函数:sgn(t)↔jω2阶跃函数:ε(t)=21+21sgn(n)↔πδ(ω)+jω1
