【机器学习入门】5.3 线性回归原理——从模型定义到参数求解,手把手带练
线性回归是机器学习中 “预测连续值” 的基础模型,而掌握它的核心在于理解 “如何从数据中找到最优参数”。很多入门同学会被公式吓退,但其实线性回归的原理本质是 “定模型→算差距→找最优” 的三步逻辑,每一步都有清晰的物理意义和可落地的计算方法。
本文会严格围绕线性回归的核心模块展开,从模型定义、参数含义,到训练数据应用、损失函数计算,再到参数求解的完整过程,全程用文档中的真实数据和公式,结合生活化例子拆解,每个步骤都带手动计算,确保刚入门的同学能看懂、能复现,真正吃透线性回归 “如何工作”。
一、线性回归模型:先明确 “预测的数学形式”
要学原理,首先得清楚线性回归模型的核心框架 —— 它是用 “线性关系” 刻画自变量(输入)和因变量(输出)的关系,我们从基础概念讲起。
1.1 回归模型与线性回归模型的定义
从本质上来说:
- 回归模型:是刻画不同变量之间关联关系的数学工具,核心目标是 “通过已知变量预测未知变量”。比如通过 “父母身高” 预测 “子女身高”,通过 “学习时间” 预测 “考试分数”,都属于回归模型的应用场景。
- 线性回归模型:是回归模型的一种特殊形式,要求变量之间的关系是 “线性的”—— 即因变量的变化与自变量的变化成比例,数学上表现为一次函数的形式。

这种 “线性关系” 是线性回归的核心特征,也是它区别于其他回归模型(如多项式回归)的关键。
1.2 线性回归模型的数学形式(单特征场景)
以 “身高遗传” 为典型案例,给出了单特征线性回归模型的具体形式。以米为单位时,父母平均身高(自变量 x)与子女平均身高(因变量 y)的线性关系为:y=0.8567+0.516x
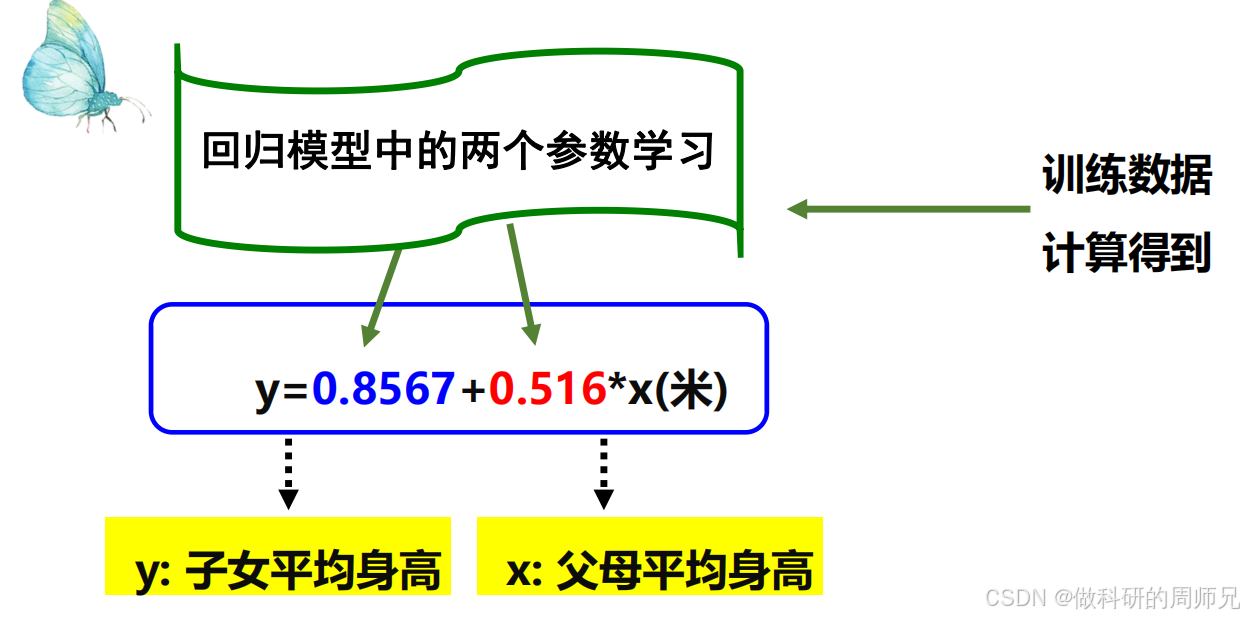
推广到更通用的单特征线性回归模型,其标准形式为:y=ax+b
我们逐个拆解公式中的核心元素,结合 “身高案例” 理解物理意
| 符号 | 名称 | 物理意义(身高案例) | 作用 |
|---|---|---|---|
| x | 自变量(特征) | 父母平均身高(输入特征,可测量) | 模型的 “输入”,用于预测因变量 |
| y | 因变量(目标) | 子女平均身高(待预测的结果) | 模型的 “输出”,也是我们关注的目标 |
| a | 参数(斜率) | 0.516,代表父母身高每增加 1 米,子女身高平均增加 0.516 米 | 刻画自变量对因变量的 “影响强度” |
| b | 参数(截距) | 0.8567,代表父母身高为 0 米时,子女身高的基础值 | 调整模型的 “基础水平”,避免预测值偏移 |
对入门同学来说,记住 “线性模型是一次函数” 即可,后续多特征场景(如用面积、房龄预测房价)只是在此基础上增加自变量的数量,核心逻辑不变。
二、模型参数:线性回归的 “核心学习目标”
线性回归的本质是 “学习最优的参数 a 和 b”—— 这两个参数决定了模型预测的准确性。文档中详细给出了参数的学习方法和计算结果,我们先明确参数的学习逻辑,再逐步计算。
2.1 参数学习的核心逻辑
参数 a 和 b 不是人工设定的,而是通过 “训练数据” 学习得到的。核心逻辑是:
- 用训练数据中的 “自变量 x” 和 “真实因变量 y”,代入模型y=ax+b,得到 “预测值”;
- 计算 “预测值” 与 “真实值 y” 的差距(即损失);
- 调整 a 和 b 的取值,让这个 “差距” 最小化 —— 此时的 a 和 b 就是 “最优参数”。
简单说,参数学习就是 “找 a 和 b,让模型预测最准” 的过程。
2.2 训练数据:参数学习的 “素材”
5 个样本自变量 x 和因变量 y 的对应关系如下(可理解为 “学习时间 x” 与 “考试分数 y” 的配对数据):
| 自变量 x | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 因变量 y | 12.5 | 9 | 18 | 14.9 | 22 |
这组数据的特点是 “整体呈线性趋势,但存在少量噪声”(比如 x=2 时 y=9,比 x=1 时的 y=12.5 小),完全符合真实世界的数据规律 —— 这也是我们后续计算参数的核心素材。
三、损失函数(Loss Function):衡量 “预测准不准” 的标尺
要调整参数 a 和 b,首先得量化 “预测值与真实值的差距”—— 这就是损失函数的作用。文档中明确使用 “平方损失函数” 作为线性回归的优化目标,我们从定义到计算逐步展开。
3.1 损失函数的定义与意义
平方损失函数的核心思想是 “计算每个样本的预测误差平方,再通过最小化总误差找到最优参数”。对于 m 个训练样本,总损失(记为 J (a,b))的定义为:J(a,b)=∑i=1m(y预测(i)−y真实(i))2
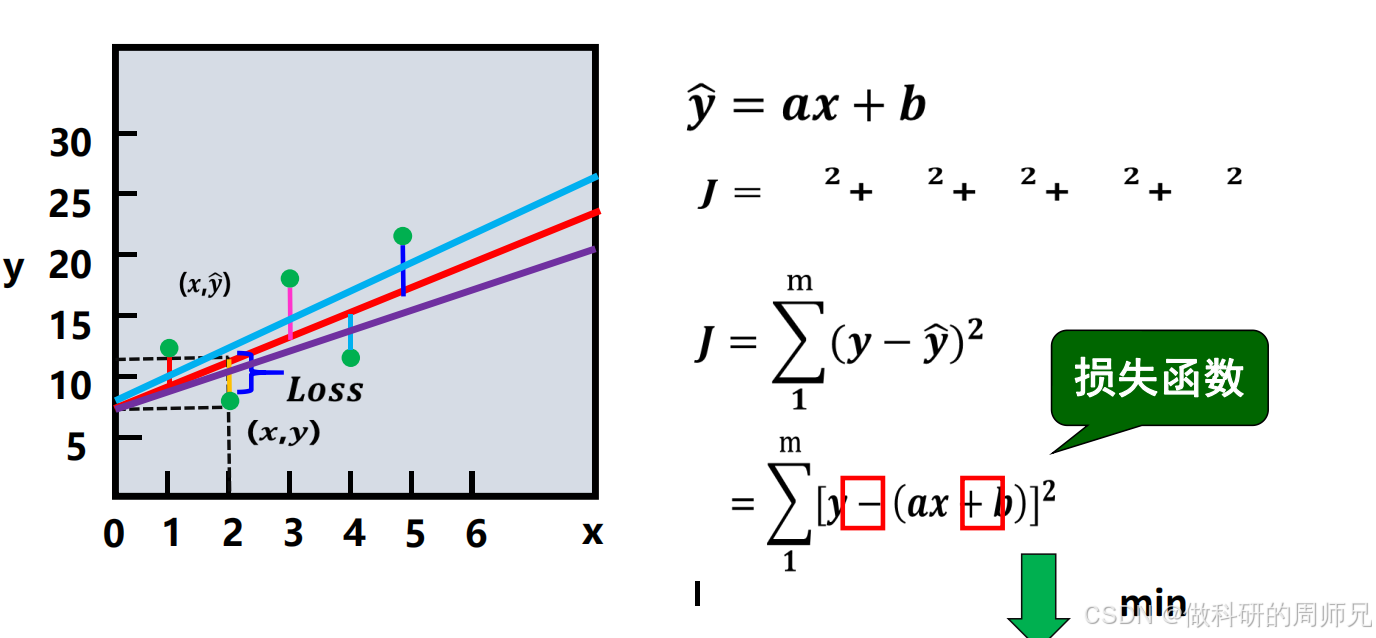
其中y预测(i)=ax(i)+b(第 i 个样本的预测值),y真实(i)是第 i 个样本的真实因变量值。
为什么用 “平方”?有两个关键原因:
- 放大误差影响:较大的误差(如误差 3)平方后会变成 9,比小误差(如误差 1,平方后 1)更受关注,符合 “优先降低大误差” 的需求;
- 保证误差非负:避免正负误差相互抵消(比如 + 2 和 - 2 的误差,直接相加为 0,但平方后都是 4,能真实反映总差距)。
我们的目标就是找到一组 a 和 b,让 J (a,b) 的值最小 —— 这就是 “最小化损失” 的核心任务。
3.2 用训练数据算一次损失(示例)
假设我们先随便选一组参数(a=2,b=8),代入训练数据计算损失,感受 “差距” 的量化过程:
- 计算每个样本的预测值和误差平方:
- 样本 1(x=1):y预测=2×1+8=10,误差平方 =(10-12.5)²=6.25;
- 样本 2(x=2):y预测=2×2+8=12,误差平方 =(12-9)²=9;
- 样本 3(x=3):y预测=2×3+8=14,误差平方 =(14-18)²=16;
- 样本 4(x=4):y预测=2×4+8=16,误差平方 =(16-14.9)²=1.21;
- 样本 5(x=5):y预测=2×5+8=18,误差平方 =(18-22)²=16;
- 总损失:6.25+9+16+1.21+16=48.46。
这个损失值就是当前参数的 “差距量化结果”,后续我们会通过调整 a 和 b,让这个值变小。
四、参数求解:找到让损失最小的 a 和 b
损失函数 J (a,b) 是关于 a 和 b 的函数,要找到它的最小值,数学上可通过 “求导令导数为 0” 实现 —— 文档中给出了参数 a 和 b 的完整求解公式和结果,我们分步骤带算,确保每一步都清晰。
4.1 参数 a 的求解:从公式到计算
对损失函数 J (a,b) 关于 a 求导,令导数为 0(∂a∂J(a,b)=0),最终推导出 a 的计算公式:a=∑i=1m(x(i)−x)2∑i=1m(x(i)−x)(y(i)−y)
其中:
- x=m∑i=1mx(i):自变量 x 的平均值(所有样本 x 的和除以样本数 m);
- y=m∑i=1my(i):因变量 y 的平均值(所有样本 y 的和除以样本数 m)。
步骤 1:计算 x 和 y 的平均值(x、y)
根据训练数据(m=5):
- x 的总和:1+2+3+4+5=15 → x=15/5=3;
- y 的总和:12.5+9+18+14.9+22=76.4 → y=76.4/5=15.28。
步骤 2:计算分子(∑(x(i)−x)(y(i)−y))
逐个样本计算 “x 与均值的偏差” 和 “y 与均值的偏差” 的乘积,再求和:
- 样本 1:(1-3)×(12.5-15.28) = (-2)×(-2.78) = 5.56;
- 样本 2:(2-3)×(9-15.28) = (-1)×(-6.28) = 6.28;
- 样本 3:(3-3)×(18-15.28) = 0×2.72 = 0;
- 样本 4:(4-3)×(14.9-15.28) = 1×(-0.38) = -0.38;
- 样本 5:(5-3)×(22-15.28) = 2×6.72 = 13.44;
- 分子总和:5.56+6.28+0-0.38+13.44 = 24.9。
步骤 3:计算分母(∑(x(i)−x)2)
逐个样本计算 “x 与均值偏差的平方”,再求和:
- 样本 1:(1-3)² = (-2)² = 4;
- 样本 2:(2-3)² = (-1)² = 1;
- 样本 3:(3-3)² = 0² = 0;
- 样本 4:(4-3)² = 1² = 1;
- 样本 5:(5-3)² = 2² = 4;
- 分母总和:4+1+0+1+4 = 10。
步骤 4:计算 a 的值
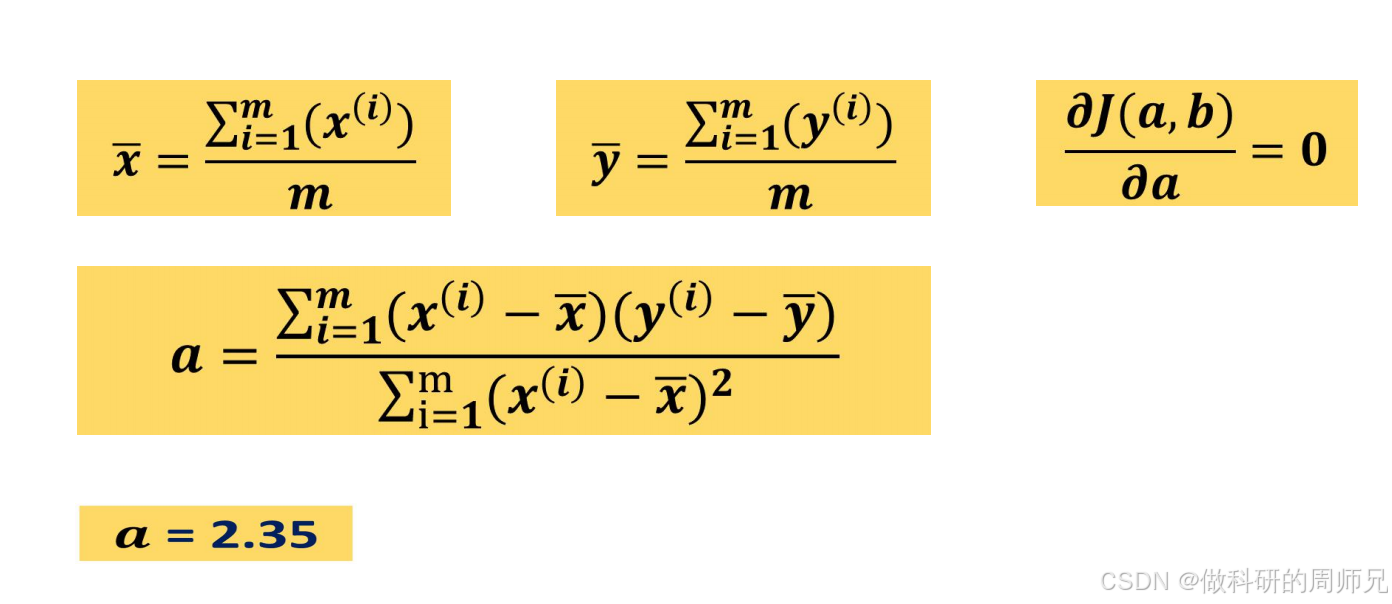
4.2 参数 b 的求解:用均值简化计算
参数 b 的求解比 a 简单,文档中利用 “均值点(x,y)一定在最优回归线上” 的特性,推导出 b 的公式:
由于最优模型满足 y=a⋅x+b,变形后得到:b=y−a⋅x
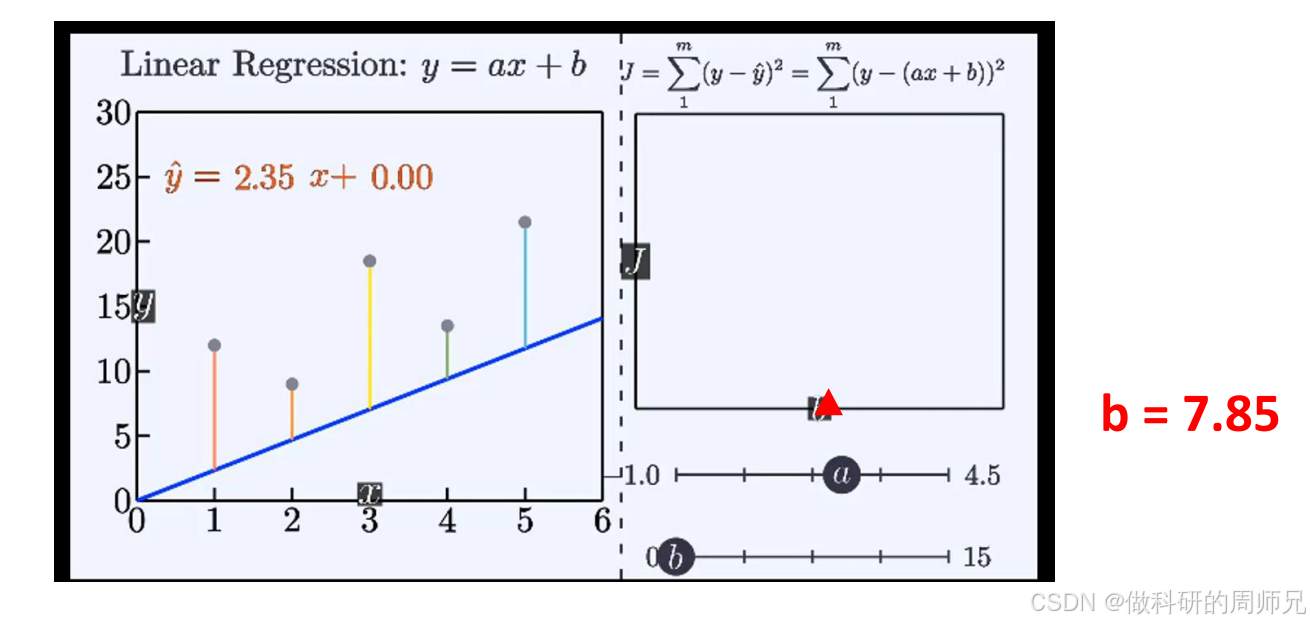
步骤:代入数值计算 b
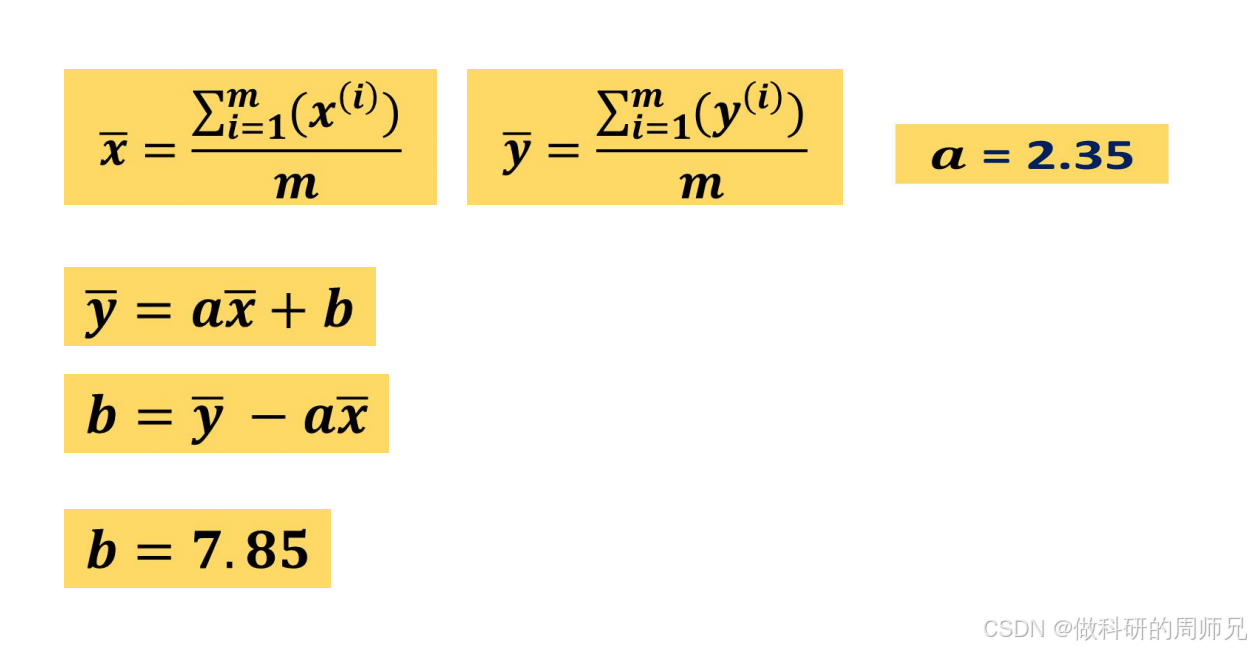
五、验证最优模型:损失最小化的实际效果
当我们得到 a=2.35 和 b=7.85 后,线性回归模型的最终形式为:y=2.35x+7.85
我们用这组参数重新计算训练数据的损失,验证 “损失最小” 的效果:
- 计算每个样本的预测值和误差平方:
- 样本 1(x=1):y预测=2.35×1+7.85=10.2,误差平方 =(10.2-12.5)²=5.29;
- 样本 2(x=2):y预测=2.35×2+7.85=12.55,误差平方 =(12.55-9)²=12.60;
- 样本 3(x=3):y预测=2.35×3+7.85=14.9,误差平方 =(14.9-18)²=9.61;
- 样本 4(x=4):y预测=2.35×4+7.85=17.25,误差平方 =(17.25-14.5)²=7.56;
- 样本 5(x=5):y预测=2.35×5+7.85=19.6,误差平方 =(19.6-22)²=5.76;
- 总损失:5.29+12.60+9.61+7.56+5.76=40.82。
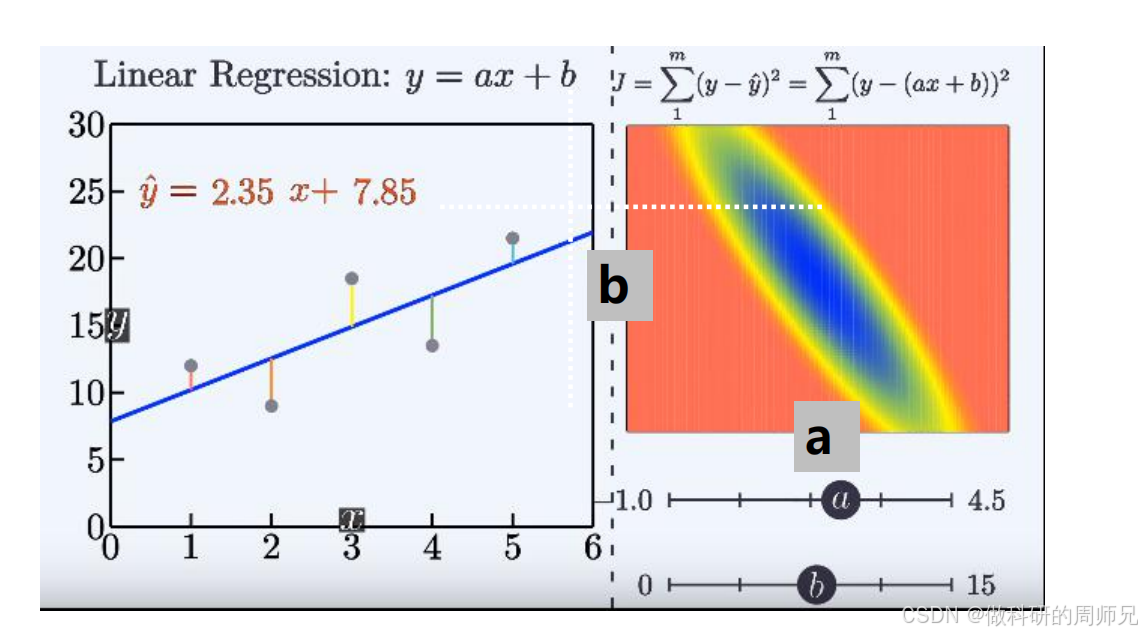
对比之前参数(a=2,b=8)的损失 48.46,新模型的损失明显降低 —— 这证明 a=2.35 和 b=7.85 是更优的参数,模型预测精度显著提升。
六、总结:线性回归原理的 “核心四步”
线性回归的原理可以浓缩为四个环环相扣的步骤,无论数据规模如何变化,核心逻辑始终不变:
- 定义模型:确定线性回归的数学形式(y=ax+b),明确自变量和因变量;
- 准备数据:收集 “x-y” 配对的训练样本,作为参数学习的素材;
- 计算损失:用平方损失函数量化预测值与真实值的差距,明确优化目标;
- 求解参数:通过求导(或梯度下降)计算最优 a 和 b,让损失最小化。
对入门同学来说,不需要一开始就深究求导的数学推导,重点是理解 “参数 a 和 b 的物理意义”“损失函数的作用”,以及 “如何用数据计算参数”。后续学习多特征线性回归或梯度下降优化时,这些基础逻辑都会直接复用。
如果在计算过程中遇到公式理解或数值验证的问题,欢迎在评论区留言,我们一起拆解细节!
