当前位置：首页 > news >正文

C语言：归并排序和计数排序

news 2025/9/5 3:35:02

一、核心思想

二、将序列拆分成许多的有序序列

三、有序序列的合并

四、归并排序的非递归的实现

五、计数排序

六、排序算法复杂度及稳定性分析

6.1、稳定性

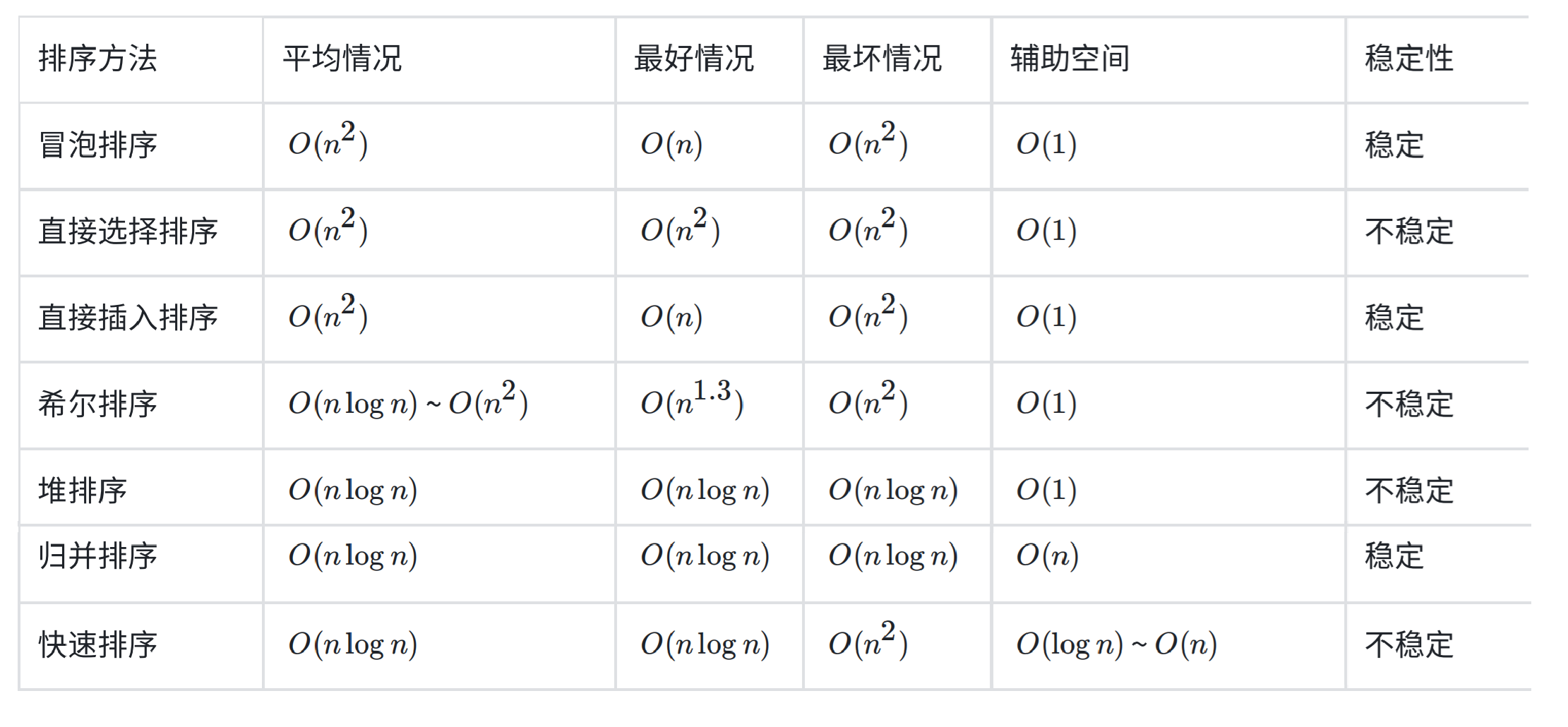
6.2、排序算法汇总

一、核心思想

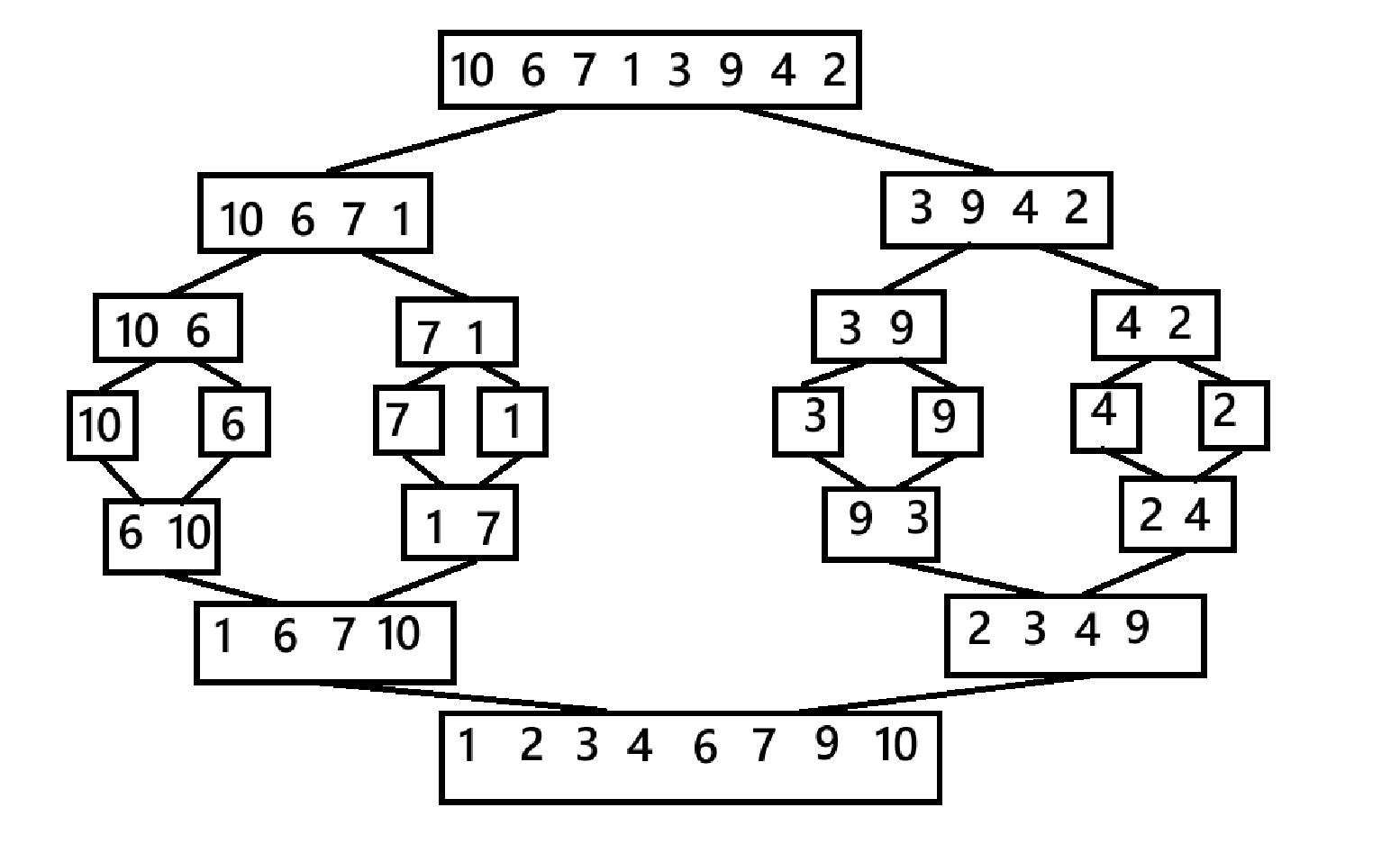
归并排序：将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列合并。那怎么得到有序序列呢？将序列分成最小单元，只有一个元素的序列就是有序的。如图：

二、将序列拆分成许多的有序序列

就是把序列拆成最小单元。怎么拆？看上面核心思想给出的构图，非常像树，那是不是要用到递归？是的，要用到递归。

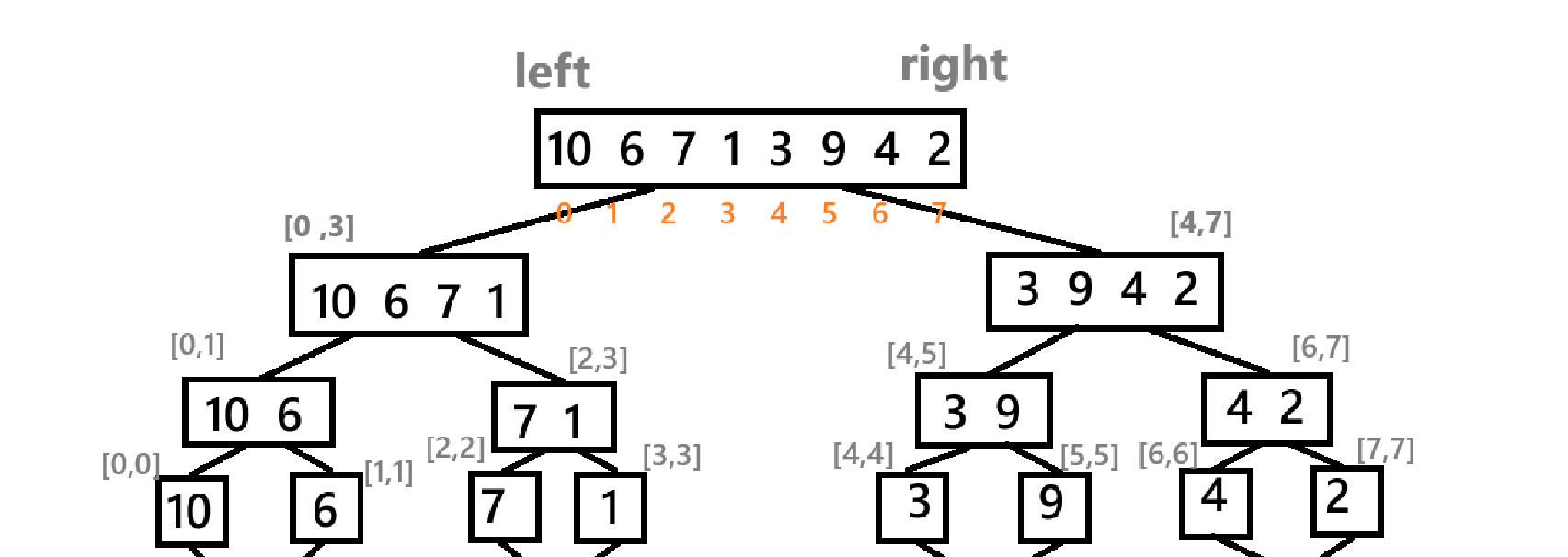
如图，拆分序列不能真的把整个序列拆分开，而是通过引入 left 和 right 来限定访问序列的范围，从而实现对序列的分割。中间元素的下标用 mid = (left+right)/2 表示，左边序列就是 [left , mid] ；右边序列就是 [mid+1 , right] 。以此类推，直到 left 不再小于 right 为止。

void _MergeSort(int* a, int left, int right)
{if (left >= right){return;}//找中间元素下标int mid = (left + right) / 2;_MergeSort(a, left, mid);_MergeSort(a, mid + 1, right);
}

三、有序序列的合并

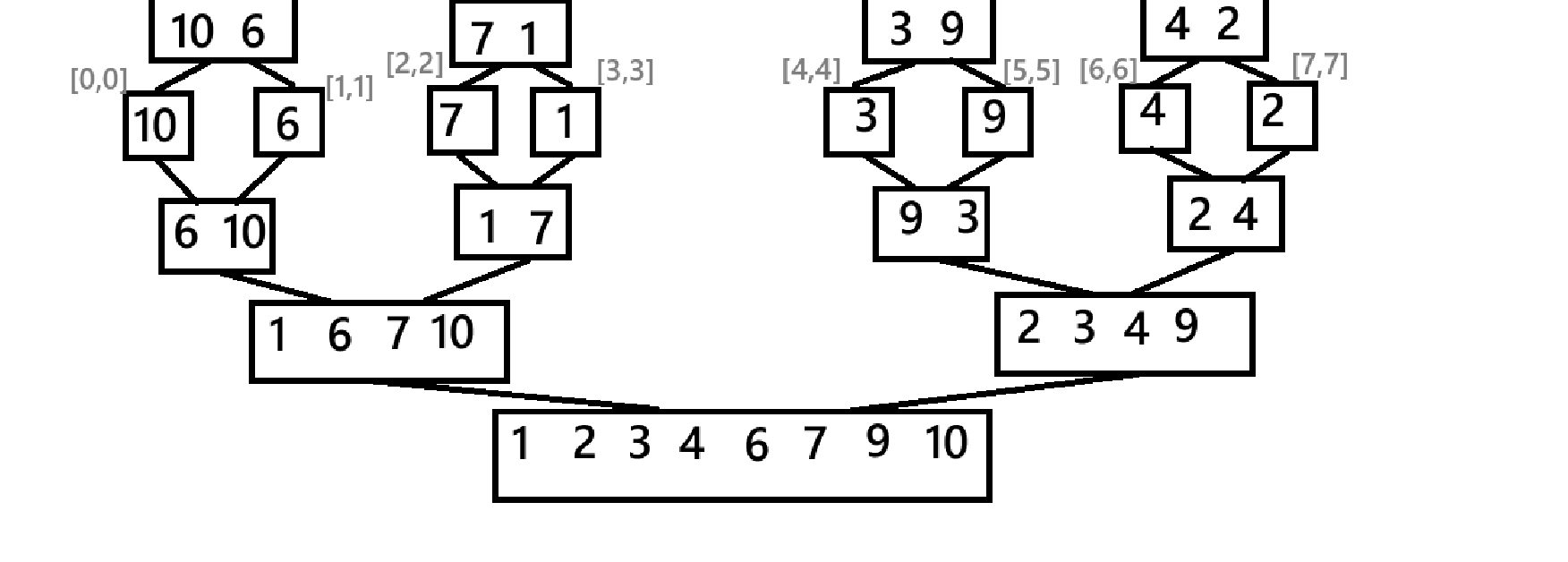
怎么合并？当然是连个有序序列谁小（大）谁放前面。放到哪里呢？如果在原数组上修改可能会导致数据覆盖而丢失，最好的办法就是创建一个临时数组存放，最后再拷贝回去即可。为了将函数封装，我们在递归函数外再套一个函数，用来创建临时数组。

void MergeSort(int* a, int n)
{assert(a);int* tmd = (int*)malloc(sizeof(int) * n);if (tmd == NULL){perror("malloc fail!");exit(1);}_MergeSort(a, 0, n - 1, tmd);free(tmd);
}

下面是合并的代码：

void _MergeSort(int* a, int left, int right, int* tmd)
{if (left >= right){return;}//找中间元素下标int mid = (left + right) / 2;_MergeSort(a, left, mid, tmd);_MergeSort(a, mid + 1, right, tmd);//合并int begin1 = left, end1 = mid;int begin2 = mid + 1, end2 = right;int index = left;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmd[index++] = a[begin1];begin1++;}else{tmd[index++] = a[begin2];begin2++;}}//走到这里，要么begin1没走完，要么begin2没走完while (begin1 <= end1){tmd[index++] = a[begin1++];}while (begin2 <= end2){tmd[index++] = a[begin2++];}//将临时数组中的序列拷贝到原序列for (int i = left; i <= right; i++){a[i] = tmd[i];}
}

最后，主包这里再给出一个递归实现的简略草图

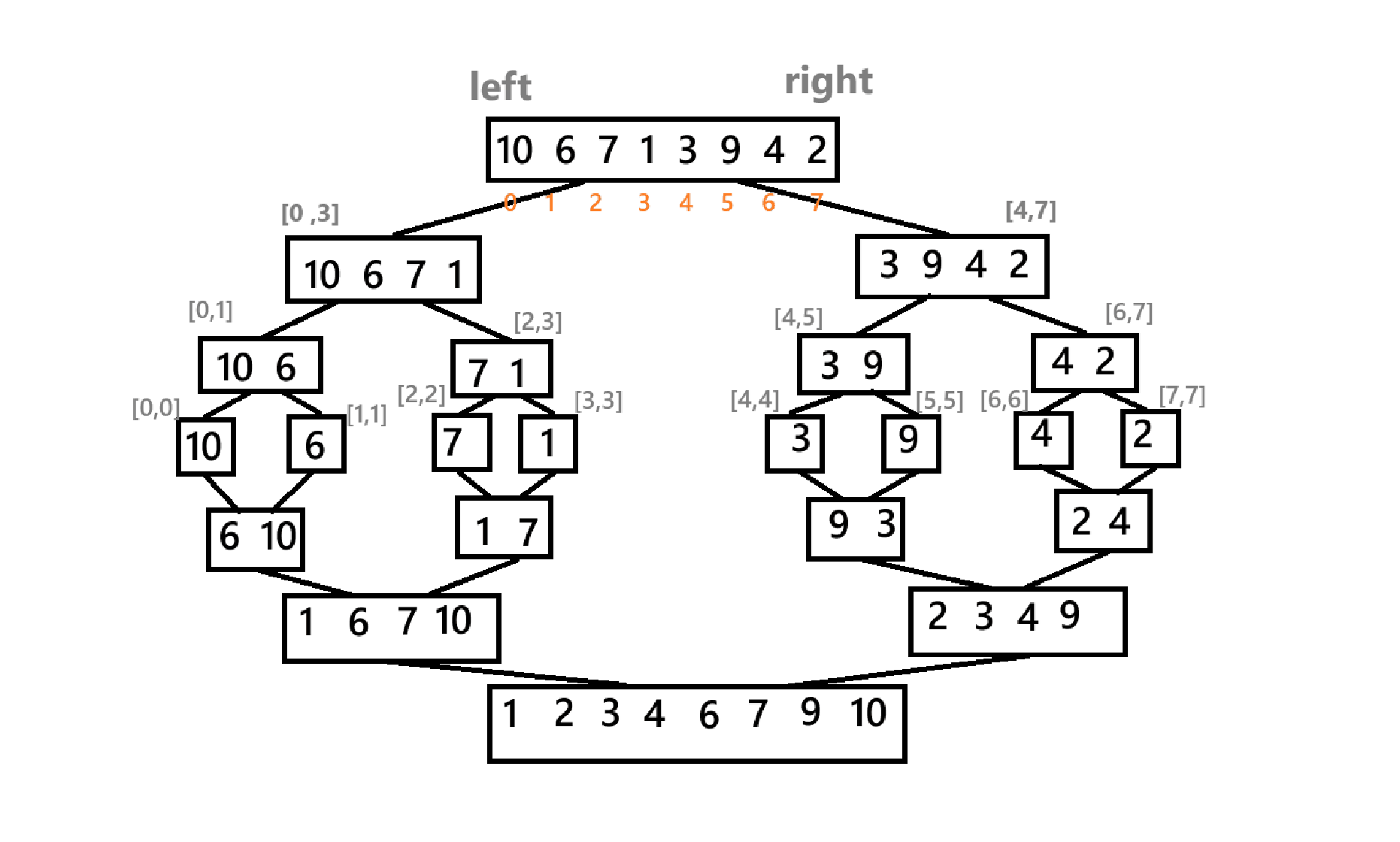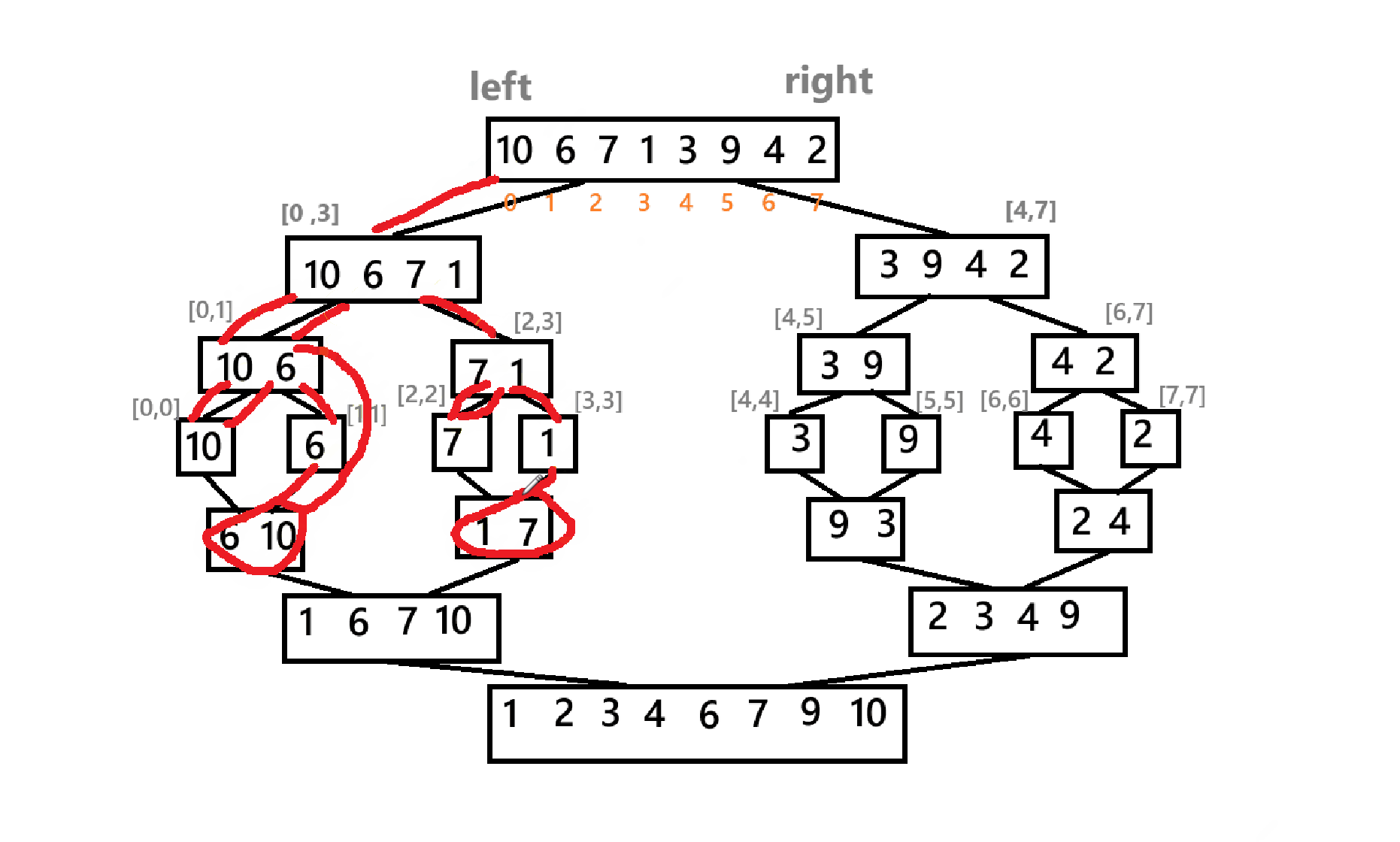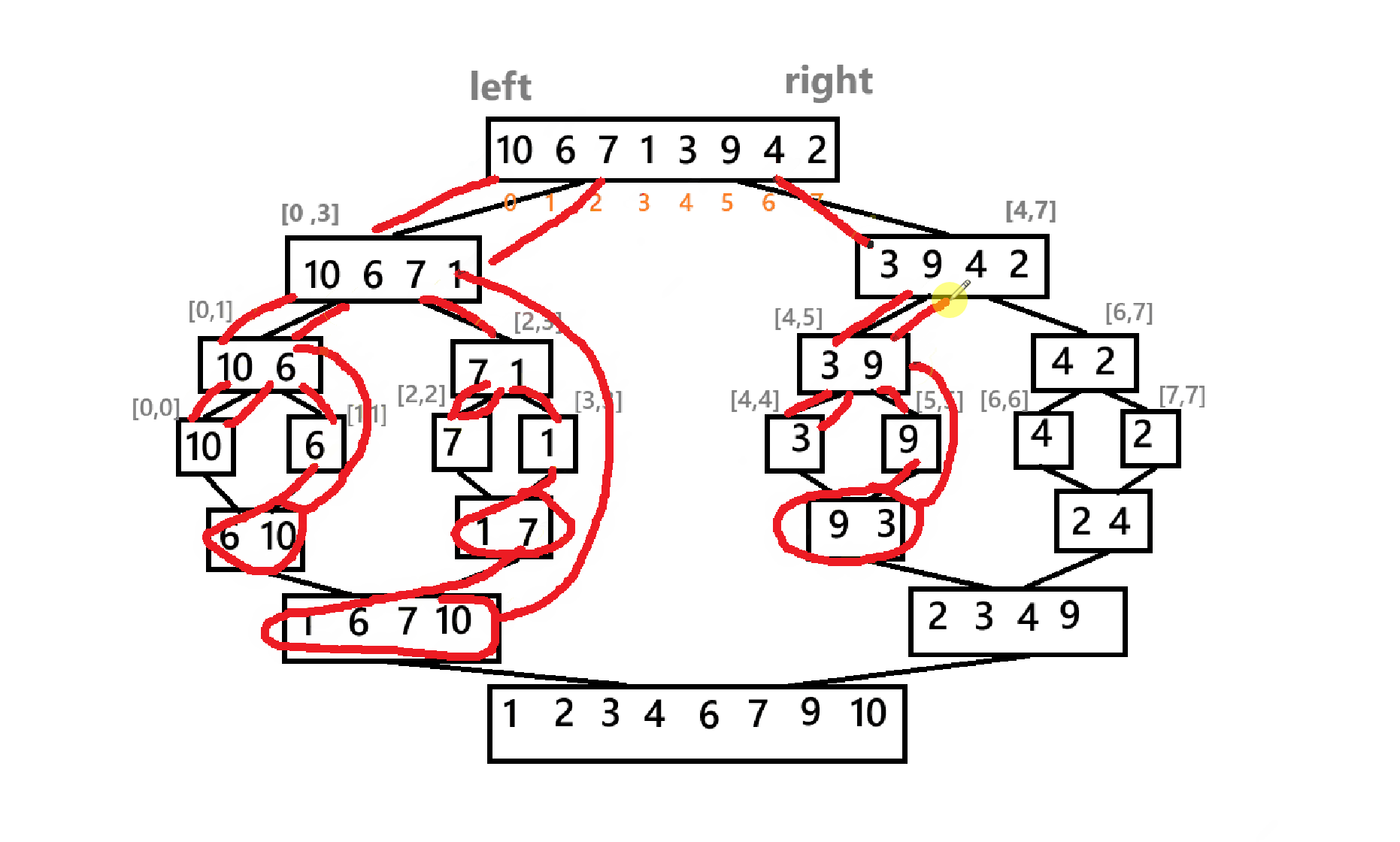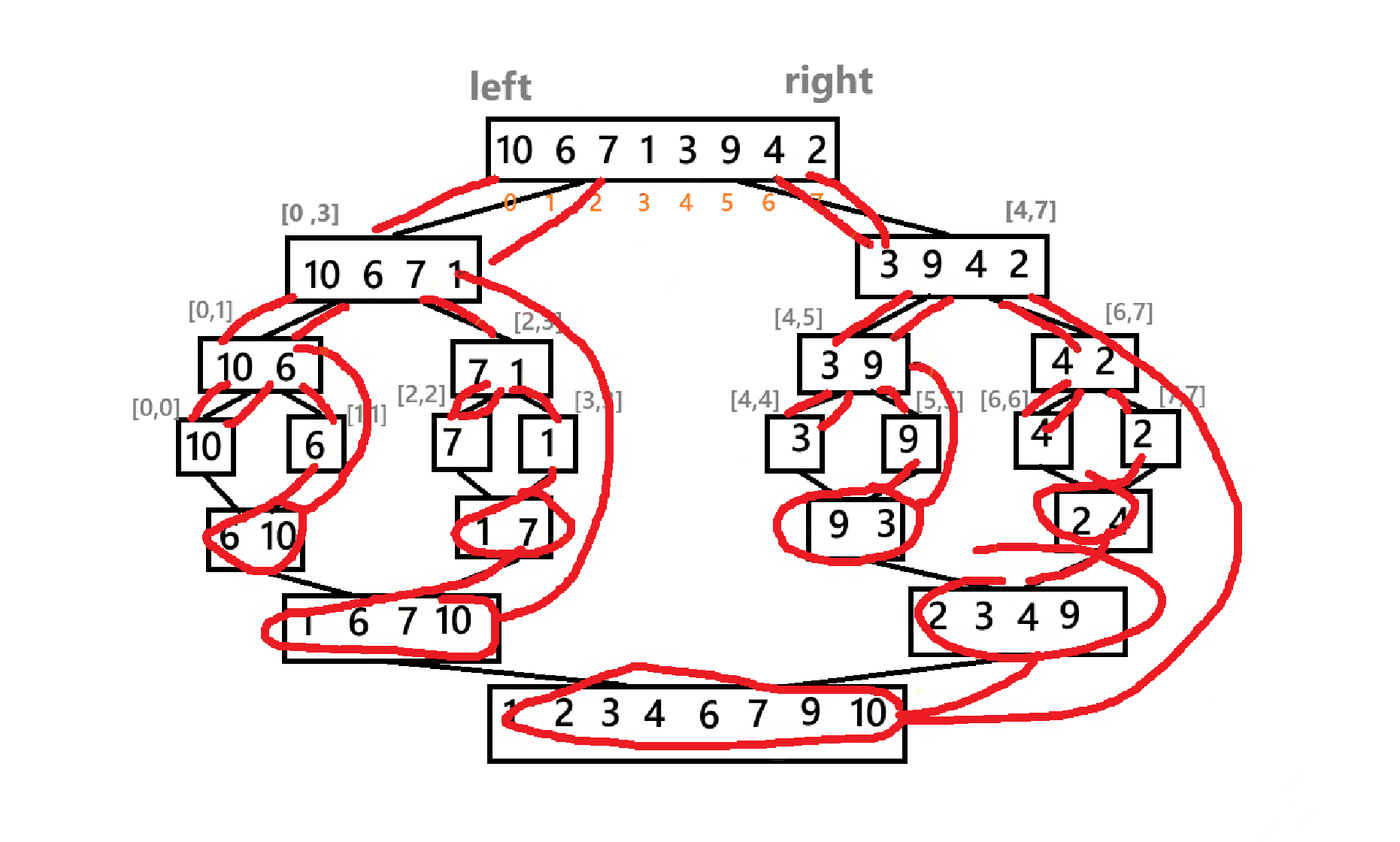
对了，归并排序的时间复杂度为：O(nlogn)

四、归并排序的非递归的实现

非递归实现难点就在于寻找有序序列并合并。

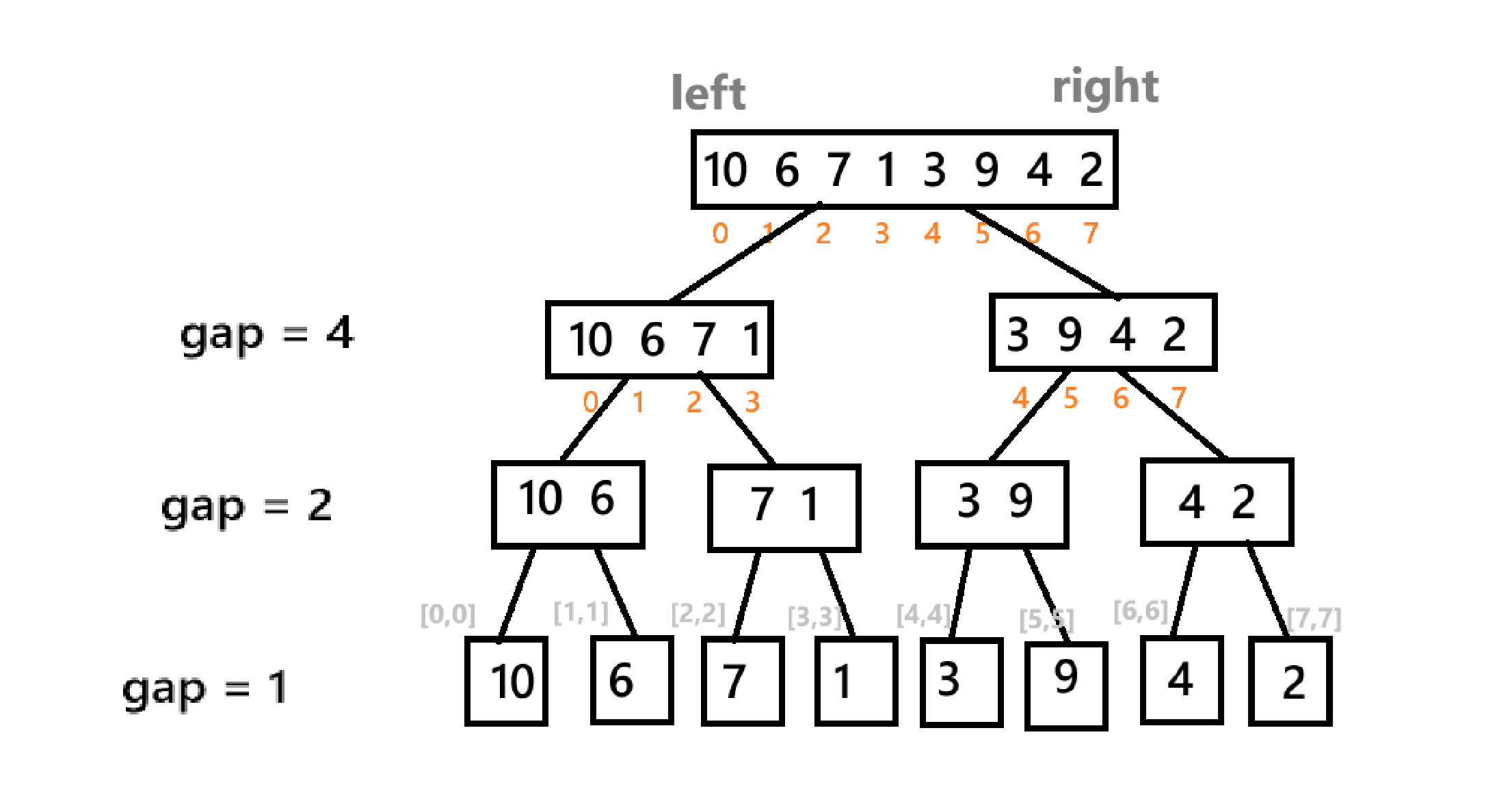
如图，设置 gap ，代表着每组有 gap 个元素。依据 gap 的划分，进行合并，所以当 gap 大于或等于元素个数时，就不用合并了。其中的分组关系由数学推导可得。

void MergeSortNonR(int* a, int n)
{assert(a);//设置临时数组int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail!");exit(1);}//引入gap划分组int gap = 1;while (gap < n){//根据gap，两两合并for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;if (begin2 >= n){break;}if (end2 >= n){end2 = n - 1;}//进行合并int index = begin1;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}while(begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1));}gap *= 2;}
}

注意：当序列个数为奇数个时，最后一个元素必定是单独成组，此时的begin2和end2 就会越界，所以要进行限制！

五、计数排序

核心思想：统计相同元素出现的次数，根据统计结构将序列回收到原来的序列中。

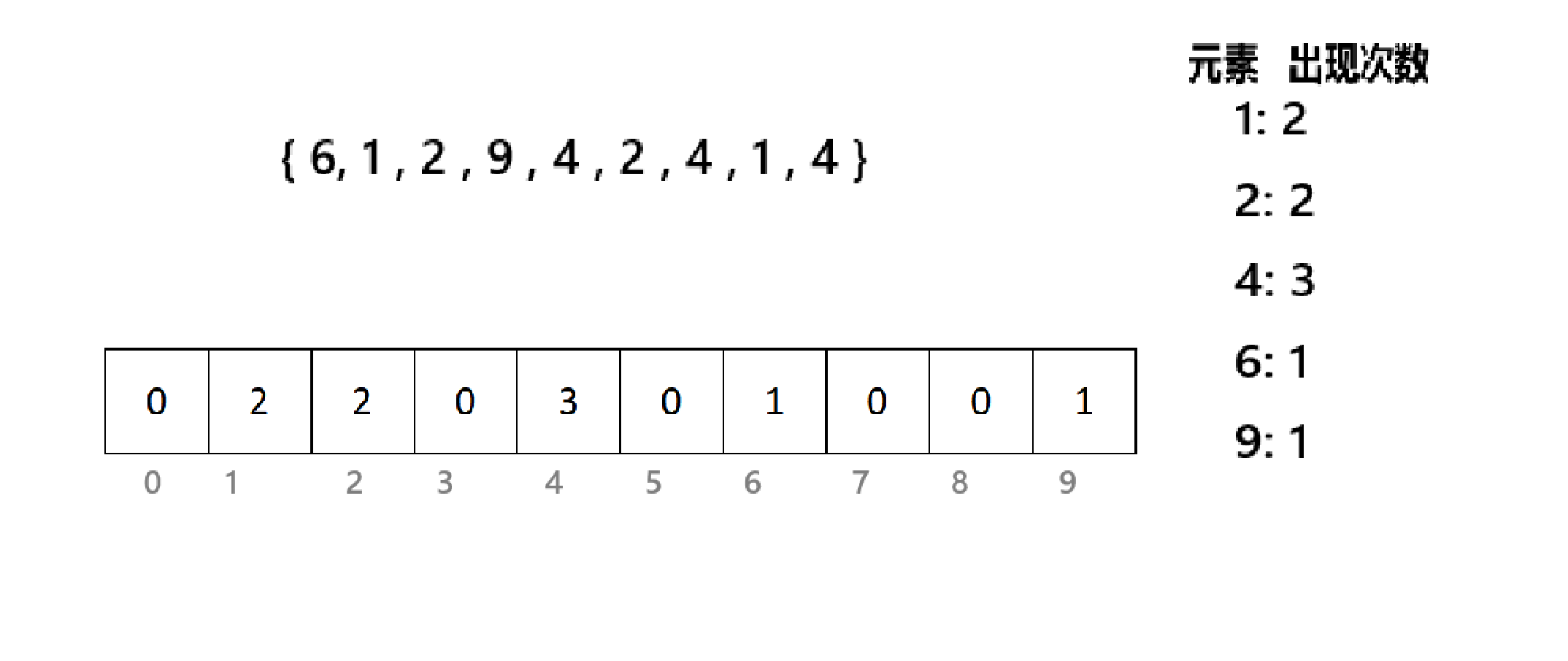
如图，将序列中各个元素出现的次数统计出来，并将次数放入数组对应的位置（把原来序列元素当做下标，出现次数当做元素）里。然后再将数组的下标依次放入原来的序列中：

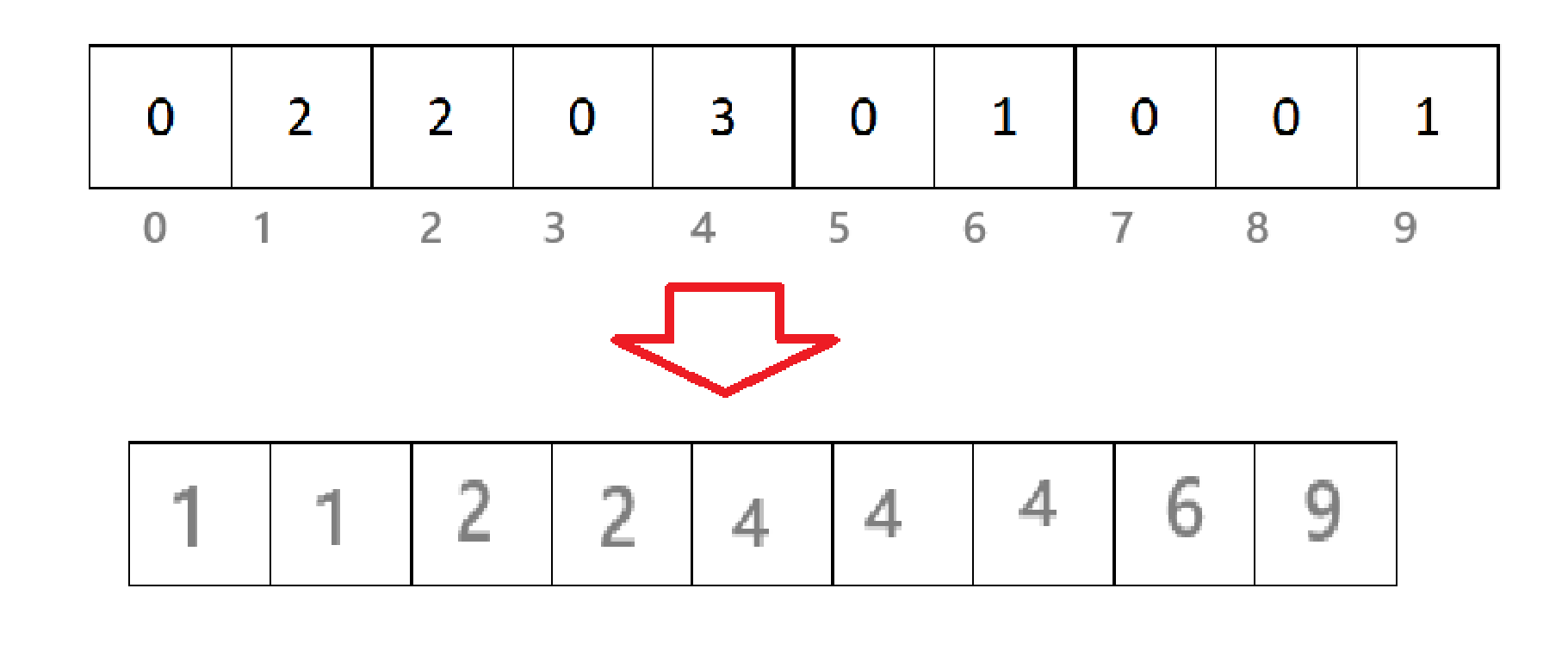
那么，如果序列中有 10005 这种非常大的数据，我们难道要创建10005个空间大小的数组吗？当然不是，找出序列中的最小值 min，然后通过数学映射的方法使得新的数组下标与原序列元素一一对应。比如：{100 ，105， 102， 104 } 这四个数据，最小值 min = 100 ，所以在下标为 0 的地方就代表着100 ，下标为2的地方代表着102，以此类推。

void CountSort(int* a, int n)
{assert(a);//寻找最小值 min 和最大值 maxint min = a[0];int max = a[0];for (int i = 0; i < n; i++){if (a[i] < min){min = a[i];}if (a[i] > max){max = a[i];}}//根据最大值和最小值确定新数组的大小 rangeint range = max - min + 1;int* count = (int*)malloc(sizeof(int) * range);if (count == NULL){perror("malloc fail!");exit(1);}//将新数组的内容全部置为0memset(count, 0, sizeof(int) * range);//统计各个元素出现的次数for (int i = 0; i < n; i++){count[a[i] - min]++;}//再将新数组的内容还原到原序列int index = 0;for (int i = 0; i < range; i++){while (count[i]--){a[index++] = i + min;}}
}