【论文阅读】Neuro-Symbolic Integration Brings Causal and Reliable Reasoning Proofs

NAACL2025

https://arxiv.org/pdf/2311.09802

作者来自阿里巴巴达摩院、港中文和善达 AI。它的核心贡献是提出了一个叫 CARING (Causal and Reliable Reasoning) 的神经符号框架，用来解决大语言模型（LLM）在复杂推理时不可靠、不可解释的问题。

摘要

在使用大语言模型（LLMs）处理复杂推理时，通常有两类方法：一类方法是通过提示 LLMs 使用各种推理结构，而这些结构化输出可以自然地被视为中间推理步骤；另一类方法是采用不依赖 LLM 的声明式求解器来完成推理任务，这类方法能带来更高的推理准确率，但由于求解器是黑箱，其推理过程缺乏可解释性。为了缓解 答案准确率和可解释性之间的权衡，我们对第二类方法提出了一个简单扩展。具体来说，我们展示了 Prolog 解释器在搜索过程中生成的中间日志是可以被访问并进一步转化为人类可读的推理证明的。只要 LLM 能够正确地将问题描述翻译成 Prolog 表示，那么对应的推理证明就能够保证具备因果性和可靠性。

在两个逻辑推理数据集和一个算术推理数据集上的实验表明，我们的框架在答案准确率和推理证明准确率上都取得了显著提升。我们的代码已开源：https://github.com/DAMO-NLP-SG/CaRing。

Intro

现有的大语言模型（LLMs）在规划能力上表现不足（Valmeekam et al., 2023; Huang et al., 2024; Kambhampati et al., 2024）。这是可以预期的，因为我们不能指望一个基于 next-token 预测 的 LLM 去解决一个需要 n 步推理 的问题——其推理空间会随着 n 的增加呈指数级增长。

针对这个问题，已有的 LLM 方法大致可以分为两类：

1. 基于搜索的 LLM 方法

   • 代表作：Self-Consistency (Wang et al., 2023)、Tree-of-Thoughts (Yao et al., 2023)、RAP (Hao et al., 2023)。

   • 思路：采用各种搜索策略（如蒙特卡洛树搜索）来迭代地提示 LLM，希望通过合适的过程监督引导搜索，从而找到正确的推理路径。

   • 优点：它们的中间推理步骤是显式的，使得推理过程具有可解释性。

   • 缺点：仍然严重依赖 LLM 自己来做规划，不能真正解决上述问题；并且每一步搜索都需要调用 LLM，而一个问题通常需要多步搜索，导致计算成本极高。

2. 基于符号求解器的方法

   • 代表作：LogicLM (Pan et al., 2023)、SatLM (Ye et al., 2023)。

   • 思路：把问题描述翻译成 声明式的符号表示（即代码），然后用现成的符号求解器执行这些表示。

   • 优点：

     1. 符号表示比推理步骤更贴近问题本身，因此 LLM 翻译问题描述 → 符号表示，比直接生成推理链要容易。

     2. 推理任务交给外部求解器执行，只要符号表示正确，就能保证推理过程的正确性。

   • 缺点：推理搜索步骤是在求解器内部隐式完成的，人类难以直接检查推理过程是否正确。

综上所述，本研究提出了一种框架，在执行推理任务时无需使用大型语言模型，但仍能生成可解释的推理步骤。我们的思路很简单：使用符号求解器进行搜索会自动记录生成的日志（即跟踪信息），这些日志在进一步处理后可以转换为人类可读的中间步骤。处理中。基于这一理念，我们采用了 Prolog 这种基于形式逻辑的声明式编程语言来实现一种方法。我们对我们的方法 CARING（因果与可靠推理）在包含推理证明注释的三个推理数据集上进行了评估，其中包括两个逻辑推理数据集，即 ProofWriter（塔夫约德等人，2021 年）和 PrOntoQA（萨帕罗夫和赫，2023 年），以及一个算术推理数据集，即 GSM8K（里贝罗等人，2023 年）。CARING 在回答准确性、推理证明相似性和推理证明准确性方面始终优于 CoT 基线和现有方法。在具有挑战性的 ProofWriter 数据集上，使用 Code-LLaMA34B 的 CARING 的回答准确率为 96.5%，推理证明相似率为 81.0%，而之前的最先进方法的准确率为 79.7%。进一步的分析表明，CARING 在推理问题变得更加复杂的情况下仍然具有稳健性。

Method

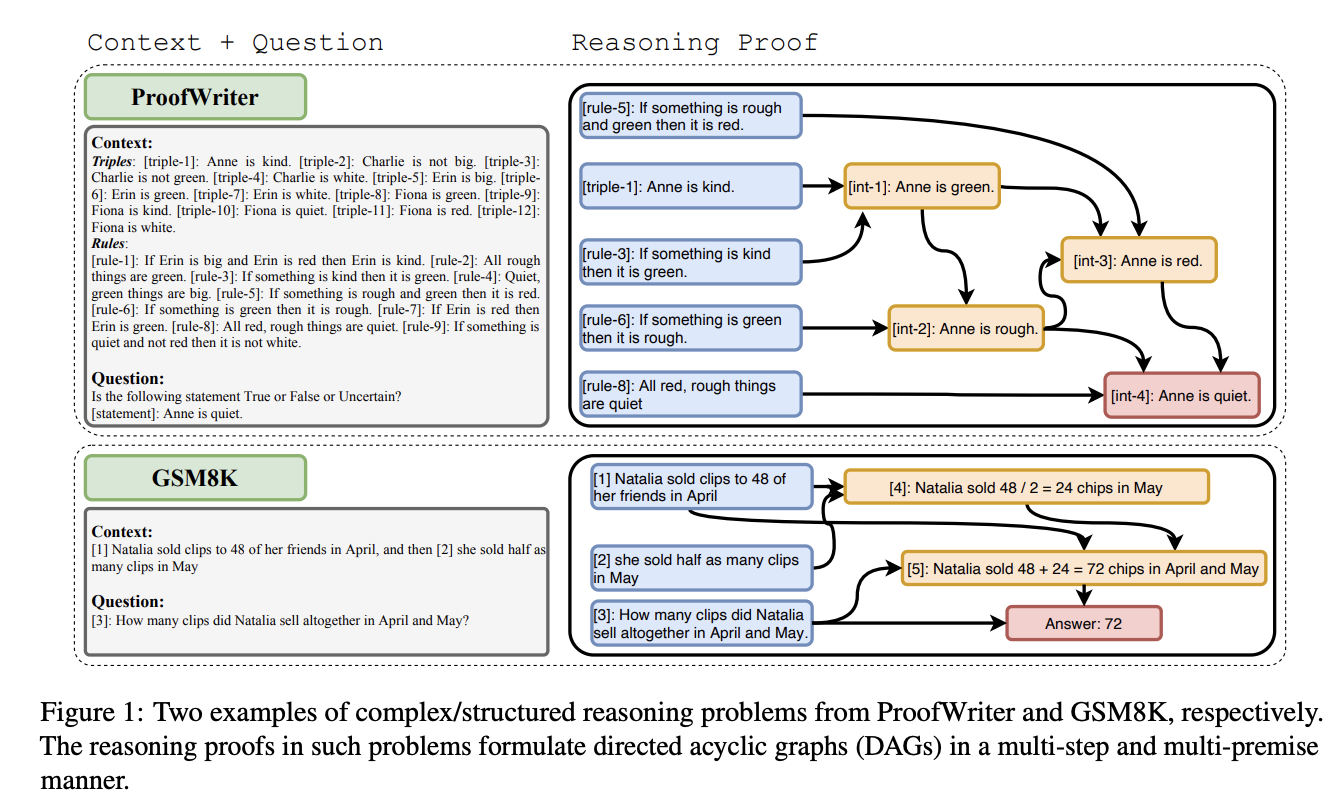我们所关注的问题具有结构化或复杂的推理特征。如图 1 所示，这些问题通常需要在有向无环图（DAG）上进行多步骤和多前提的推理，其中各个节点代表不同的知识片段，有向边表示推理步骤。每个推理步骤都利用现有的知识来推断新的相关知识。通常会将众多知识片段聚合起来以推导出一个新的知识片段，我们将其称为“多前提”。求解器通常会执行多个这样的步骤以达到最终目标，我们将其称为“多步骤”。整个推理过程自然地构成了一个 DAG。

我们希望为这类推理问题提供准确的答案以及因果性和可靠的解释。科瓦尔斯基（1979 年）提出，算法 = 逻辑 + 控制，其中逻辑指的是可用于解决问题的知识，而控制指的是可以利用这些知识的解决问题的策略。他们进一步证明，算法从逻辑组件和控制组件的分离中受益。现有的采用符号求解器来寻找有效推理路径的研究都遵循了这一设计原则（潘等人）2023 年；（Ye 等人，2023 年）。我们的工作也遵循了这一原则。
我们提出了 CARING（因果与可靠推理）这一模块化方法，它由两个部分组成。组件：
• SYMGEN：基于语言模型的符号表示生成器（第 3.1 节），它将问题描述转换为形式化的符号知识表示形式，这些表示可用于符号推理。
• SYMINFER：无语言模型支持的符号推理引擎（第 3.2 节），它通过执行由 SYMGEN 提供的符号表示来进行有意识的推理。借助定制的 Prolog 元解释器，SYMINFER 支持（i）因果性和可靠的推理过程追踪（第 3.2.1 节）；（ii）各种搜索策略，如深度优先搜索（DFS）和迭代加深搜索（IDS）（第 3.2.2 节）。
SYMINFER 的机器执行特性确保了因果性和可靠性，如图 3 所示。根据因果性原则，新知识片段的推理严格与那些相关的现有片段紧密相关，从而确保精确且有限的归属。这意味着只有当前一个事件（边的基点）直接影响下一个事件（顶点）时，才会建立因果关系。关于可靠性，每个新推断节点内的内容都是一个确定性的过程的结果，从而使其免受各种情况的影响。在大型语言模型的输出中，经常会遇到一些错误的幻觉现象。

3.1 SYMGEN：符号表示生成器
为了表示逻辑（即可用于解决问题的知识），我们采用了一种流行的逻辑编程语言——Prolog（科尔马鲁尔和鲁塞尔，1996 年）。Prolog 是一种声明式编程语言，在这种语言中，逻辑被表示为关系（称为事实和规则），表 1 中展示了几个示例。通过对这些关系运行查询来启动计算，这将在第 3.2 节中进一步解释。
尽管 LLM 在组合新知识（即生成推理步骤）时容易产生错误的事实，但它们在理解自然语言并将其直接转换为其他格式方面表现出强大的能力（叶和杜雷特，2022 年；萨帕罗夫和赫，2023 年）。提示 LLM 将问题描述转换为符号表示，恰好利用了 LLM 的这一强大特性，正如叶等人（2023 年）之前所展示的那样。至于实现方式，我们使用了几条人工撰写的上下文示例来训练小样本提示 LLM，每个示例都包含一个问题及其对应的 Prolog 表示。