8.30美团技术岗算法第二题
题目


说明
这题属于基础知识题,考察点:
1、Fisher线性判别器
2、pytorch构造神经网络架构
知识点
零、Fisher线性判别器:
Fisher 线性判别器(FLD)是由英国统计学家 Ronald Fisher 于 1936 年提出的经典线性判别方法,核心思想是通过一条直线(二维)或一个超平面(高维)将不同类别的数据 “最优分离”—— 即最大化类间差异、最小化类内差异,从而实现对数据的分类。它是模式识别、机器学习领域中线性分类器的基础,也是理解 “降维 + 分类” 融合思路的关键模型。
一、FLD 的核心目标:什么是 “最优线性分离”?
FLD 解决的是二分类问题(多分类可通过 “一对多”“一对一” 扩展),其核心逻辑是:将高维数据投影到一条直线(一维空间)上后,让两类数据在投影后的空间中 “分得最开”。
具体来说,“最优分离” 需同时满足两个条件:
- 类间距离最大:两类数据在投影后的 “中心(均值)” 距离尽可能远;
- 类内距离最小:每一类数据在投影后的 “离散程度(方差)” 尽可能小。
举个直观例子:假设两类数据(如 “猫” 和 “狗” 的图像特征)在高维空间中混合分布,FLD 会找到一个投影方向,使得投影后 “猫” 的所有点都集中在一个区域,“狗” 的所有点集中在另一个区域,且两个区域间隔最大 —— 这样只需在投影后的直线上画一条阈值线,就能轻松区分两类数据。
二、FLD 的数学推导:如何找到 “最优投影方向”?
FLD 的本质是求解一个投影向量 w(高维空间中的直线方向),将高维数据 x(维度为 d)投影到一维空间,投影后的数据为 y=wTx(y 是标量)。推导过程围绕 “最大化目标函数” 展开。
1. 定义核心数学量
首先定义二分类问题中的基础统计量(假设数据分为两类:C1 和 C2):
| 符号 | 含义 |
|---|---|
| N1,N2 | 类别 C1、C2 的样本数量 |
| μ1,μ2 | 类别 C1、C2 在高维空间中的均值向量(维度 d×1) |
| S1,S2 | 类别 C1、C2 的类内散度矩阵(维度 d×d) |
| Sw=S1+S2 | 总类内散度矩阵(衡量两类数据的整体离散程度) |
| Sb=(μ1−μ2)(μ1−μ2)T | 类间散度矩阵(衡量两类均值的差异程度) |
关键矩阵的具体计算
类内散度矩阵 Si(描述单个类内样本与类均值的偏离):
对类别 Ci,每个样本 xj∈Ci,则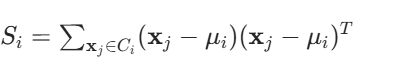
直观理解:Si 越大,说明该类数据在高维空间中越分散。类间散度矩阵 Sb(描述两类均值的差异):
由于 μ1−μ2 是 d×1 向量,其外积 (μ1−μ2)(μ1−μ2)T 是 d×d 矩阵,且秩为 1(仅包含两类均值的差异信息)。
2. 投影后的统计量
当数据通过 w 投影到一维空间后,上述统计量对应变为:
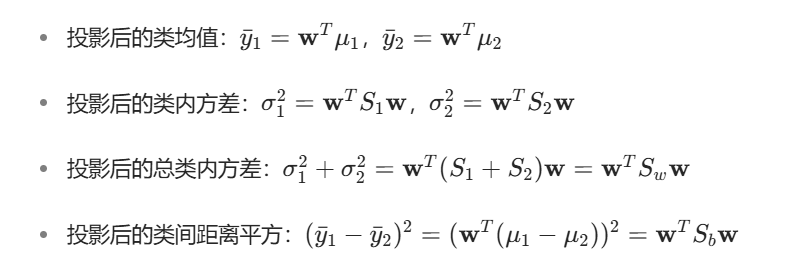
3. Fisher 准则函数:最大化 “类间 / 类内” 比

4. 最优投影向量的最终形式
综上,FLD 的最优投影向量为:
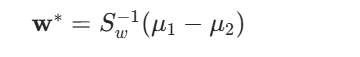
注意:w∗ 的 “方向” 是关键(决定投影效果),其 “长度” 不影响投影结果(因为投影 y=wTx 对 w 成比例缩放后,y 也成比例缩放,类间 / 类内比不变),因此实际应用中无需关注 w∗ 的长度。
三、FLD 的分类流程(完整步骤)
得到最优投影向量 w∗ 后,FLD 的分类过程可分为 3 步:
步骤 1:训练阶段 —— 计算 w∗ 和分类阈值 y0

步骤 2:测试阶段 —— 对新样本分类

四、FLD 的特点与局限性
1. 核心优点
- 降维与分类结合:将高维数据投影到一维空间,既简化了计算,又保留了 “最优分离” 的关键信息,适合高维小样本场景(如早期图像识别);
- 理论简洁且可解释:最优投影向量直接由数据的均值和散度矩阵决定,物理意义明确(最大化类间 / 类内比);
- 计算成本低:仅需计算均值、散度矩阵及其逆,无迭代过程,训练速度快。
2. 主要局限性
- 仅支持二分类:FLD 原生是二分类模型,多分类需通过 “一对多”(One-vs-Rest)或 “一对一”(One-vs-One)扩展,且扩展后效果可能下降;
- 假设数据近似正态分布:FLD 隐含 “两类数据服从同协方差矩阵的正态分布” 假设,若数据分布严重偏离正态(如非凸、多峰),分离效果会变差;
- 对异常值敏感:类内散度矩阵 Sw 受异常值影响较大,若训练集中有极端异常值,会导致 Sw 估计偏差,进而影响 w∗ 的准确性;
- 线性可分假设:FLD 是线性模型,若两类数据在原始空间中非线性可分(如 “异或” 问题),仅通过线性投影无法实现有效分离,此时需结合核方法(如核 Fisher 判别器,Kernel FLD)。
五、FLD 与其他线性分类器的对比
为了更清晰地理解 FLD 的定位,下表对比了 FLD 与逻辑回归(Logistic Regression)、线性支持向量机(Linear SVM)的核心差异:
| 对比维度 | Fisher 线性判别器(FLD) | 逻辑回归(Logistic Regression) | 线性支持向量机(Linear SVM) |
|---|---|---|---|
| 核心目标 | 最大化投影后的类间 / 类内比(基于数据分布) | 最大化分类概率的对数似然(基于概率模型) | 最大化两类样本到超平面的最小距离(间隔最大化) |
| 概率输出 | 无(仅硬分类) | 有(输出属于某类的概率) | 无(原生仅硬分类,可通过 Platt 缩放扩展概率) |
| 处理非线性 | 原生不支持(需核方法扩展) | 原生不支持(需特征映射扩展) | 支持(通过核方法,如 RBF 核) |
| 对样本数量的敏感 | 适合小样本(高维小样本优势明显) | 适合大样本(样本量越大,概率估计越准) | 对样本数量不敏感,但大样本下计算成本高 |
| 应用场景 | 高维小样本、降维优先的分类任务(如早期模式识别) | 需概率解释的分类任务(如风险评估、医疗诊断) | 追求高分类精度、线性可分 / 近似可分场景(如文本分类) |
六、FLD 的扩展与应用
1. 核 Fisher 判别器(Kernel FLD)
为解决 FLD 无法处理非线性数据的问题,核 FLD 引入核方法:通过核函数(如 RBF 核、多项式核)将原始高维数据映射到更高维的特征空间,在特征空间中构建线性 FLD,从而实现对原始空间中非线性数据的分离。核 FLD 保留了 FLD 的简洁性,同时提升了对非线性数据的适应能力。
2. 典型应用场景
- 早期模式识别:如手写数字识别(MNIST 数据集的早期基线模型)、字符分类;
- 生物特征识别:如人脸识别(将人脸图像的高维像素特征投影到一维,实现身份验证);
- 高维小样本数据分类:如基因数据、光谱数据的分类(样本量少但维度极高,FLD 的降维优势可充分发挥)。
七、总结
Fisher 线性判别器是线性分类与降维领域的经典模型,其核心思想 “最大化类间差异、最小化类内差异” 为后续的判别式模型(如 SVM)奠定了基础。尽管 FLD 存在 “仅支持二分类”“线性可分假设” 等局限性,但在高维小样本、数据近似正态分布的场景中,仍具有不可替代的优势。
理解 FLD 的推导过程(尤其是 Fisher 准则函数与瑞利商的关系),不仅能掌握其应用方法,更能深入理解 “判别式学习” 的核心逻辑 —— 从数据的统计特性出发,直接优化分类性能,而非先建模数据分布(生成式模型思路)。
代码
import numpy as np
import json
from typing import Tuple, Listclass FisherLDA:"""Fisher线性判别分析(Linear Discriminant Analysis, LDA)实现用于二分类问题的降维和分类"""def __init__(self, reg_param: float = 1e-6):"""初始化LDA分类器Args:reg_param: 正则化参数,用于避免奇异矩阵"""self.reg_param = reg_paramself.w = None # 投影向量self.mu0 = None # 类别0的均值self.mu1 = None # 类别1的均值self.m0 = None # 训练集中类别0的投影均值self.m1 = None # 训练集中类别1的投影均值def _compute_class_means(self, X: np.ndarray, y: np.ndarray) -> Tuple[np.ndarray, np.ndarray]:"""计算各类别的均值向量Args:X: 特征矩阵 (n_samples, n_features)y: 标签向量 (n_samples,)Returns:mu0, mu1: 两个类别的均值向量"""# 类别0的样本X0 = X[y == 0]N0 = len(X0)mu0 = np.sum(X0, axis=0) / N0 if N0 > 0 else np.zeros(X.shape[1])# 类别1的样本X1 = X[y == 1]N1 = len(X1)mu1 = np.sum(X1, axis=0) / N1 if N1 > 0 else np.zeros(X.shape[1])return mu0, mu1def _compute_within_class_scatter(self, X: np.ndarray, y: np.ndarray, mu0: np.ndarray, mu1: np.ndarray) -> np.ndarray:"""计算类内散度矩阵 S_WArgs:X: 特征矩阵y: 标签向量mu0, mu1: 两个类别的均值向量Returns:S_W: 类内散度矩阵"""n_features = X.shape[1]S_W = np.zeros((n_features, n_features))# 计算类别0的散度for i in range(len(X)):if y[i] == 0:diff = (X[i] - mu0).reshape(-1, 1)S_W += diff @ diff.Telif y[i] == 1:diff = (X[i] - mu1).reshape(-1, 1)S_W += diff @ diff.Treturn S_Wdef fit(self, X: np.ndarray, y: np.ndarray):"""训练LDA模型Args:X: 训练特征矩阵 (n_samples, n_features)y: 训练标签向量 (n_samples,), 值为0或1"""# 1. 计算类别均值self.mu0, self.mu1 = self._compute_class_means(X, y)# 2. 计算类内散度矩阵S_W = self._compute_within_class_scatter(X, y, self.mu0, self.mu1)# 3. 添加正则化项避免奇异S_W_reg = S_W + self.reg_param * np.eye(S_W.shape[0])# 4. 计算投影向量 w = (S_W_reg)^(-1) * (mu1 - mu0)try:self.w = np.linalg.solve(S_W_reg, (self.mu1 - self.mu0))except np.linalg.LinAlgError:# 如果仍然奇异,使用伪逆self.w = np.linalg.pinv(S_W_reg) @ (self.mu1 - self.mu0)# 5. 计算训练集中两类的投影均值self.m0 = self.w.T @ self.mu0self.m1 = self.w.T @ self.mu1def predict(self, X: np.ndarray) -> np.ndarray:"""对测试样本进行预测Args:X: 测试特征矩阵 (n_samples, n_features)Returns:predictions: 预测标签 (n_samples,)"""if self.w is None:raise ValueError("模型尚未训练,请先调用fit方法")# 将样本投影到一维z = X @ self.w# 分类规则:比较与两类投影均值的距离predictions = np.zeros(len(X), dtype=int)for i in range(len(X)):dist_to_class0 = abs(z[i] - self.m0)dist_to_class1 = abs(z[i] - self.m1)predictions[i] = 1 if dist_to_class1 < dist_to_class0 else 0return predictionsdef parse_input(input_str: str) -> Tuple[np.ndarray, np.ndarray, np.ndarray]:"""解析JSON格式的输入数据Args:input_str: JSON格式的输入字符串Returns:X_train, y_train, X_test: 训练特征、训练标签、测试特征"""data = json.loads(input_str.strip())# 解析训练数据train_data = np.array(data['train'])X_train = train_data[:, :-1] # 前m列为特征y_train = train_data[:, -1].astype(int) # 最后一列为标签# 解析测试数据X_test = np.array(data['test'])return X_train, y_train, X_testdef main():"""主函数:读取输入,训练模型,输出预测结果"""# 读取输入input_str = input().strip()try:# 解析数据X_train, y_train, X_test = parse_input(input_str)# 创建并训练LDA模型lda = FisherLDA(reg_param=1e-6)lda.fit(X_train, y_train)# 预测测试样本predictions = lda.predict(X_test)# 输出结果result = predictions.tolist()print(json.dumps(result))except Exception as e:# 错误处理print(f"错误: {str(e)}")returnif __name__ == "__main__":main()