FDTD_梯度波导学习（1）

项目6.1 阶跃折射率型和渐变折射率型光纤（FDE）

本主题将阶跃折射率和渐变折射率光纤的解析解与 FDE 求解器模拟的结果进行了比较。

模拟设置

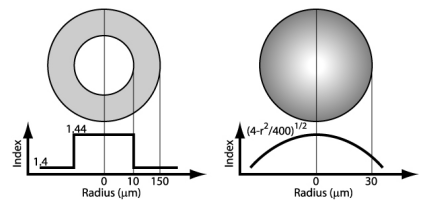
上图展示了阶跃折射率（左）和渐变折射率（右）光纤的几何形状和折射率分布。

阶跃折射率光纤在 1.55 微米波长下进行了测试，而渐变折射率光纤在 1 微米波长下进行了测试。阶跃折射率光纤是通过两个重叠的二氧化硅（折射率 n=1.4）圆结构和折射率 n=1.44 的电介质结构创建的。渐变折射率光纤是通过一个折射率由方程 sqrt(4*(1-(x^2+y^2)/40^2)) 给出的圆结构创建的。

结果

分析解

 对于阶跃折射率光纤中的 TM 模式，其分析解可通过 MATLAB 脚本 step_index_fiber.m 计算得出；或者您也可以下载包含计算结果的文本文件 step_index_fiber.txt。在渐变折射率光纤中，TE 模式的有效折射率的分析解由以下表达式给出：

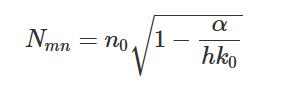
其中：

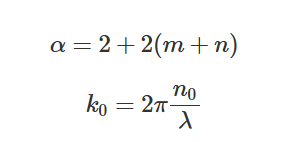
这些分析结果将在下一节用于验证 FDE 计算。

阶跃折射率光纤

脚本 step_index_fiber.lsf 计算 TM01、TM02 和 TM03 模式的有效折射率，并绘制相对于分析结果的误差，作为网格点数的函数。文件 step_index_fiber.ldf 包含先前计算并保存在 d-cards 中的这些模式，这些模式由脚本导入，并使用 bestoverlap 函数识别所需的模式。该脚本还允许您运行有效折射率的分析计算，并使用 Matlab 生成误差图。要启动 Matlab 计算（必须启用 Matlab 集成），应将标志“use_matlab”设置为 1。以下结果是使用“共形变体 1”进行网格细化选项计算得出的（在脚本中设置 conformal_mesh_on=1）。由于阶梯效应，不使用共形网格时结果的准确性会降低。

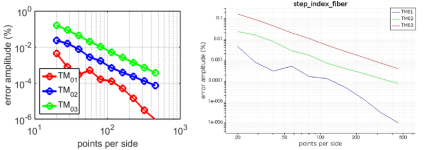
左）在波长为 1.55 微米时，阶跃折射率光纤的 TM 模式下 MODE 计算误差的大小与解析结果的对比。x 轴表示计算区域每边的网格点数。（右）仅使用内置的 MODE 函数（无 Matlab 接口）生成的相同图形。

渐变折射率光纤

脚本graded_index_fiber.lsf计算TE01和TE11模式的有效折射率，并绘制相应的误差与分析结果的函数关系图，作为网格点数量的函数。文件graded_index_fiber.ldf包含这些先前计算并在d卡中保存的模式，该脚本导入它们并用函数bestoverlap识别所需的模式。该脚本还探索了TE01模式的色散特性和相关误差。

与之前一样，您可以使用Matlab生成散布图和误差图。要将“use_matlab”标志设置为1以启动Matlab计算（必须启用Matlab集成）

在这种情况下，共形网格对结果的准确性没有显著影响，因为光纤中的索引变化平滑，而不是阶跃索引光纤中的突然变化。下面的结果是使用“共形变体1”选项计算得出的。

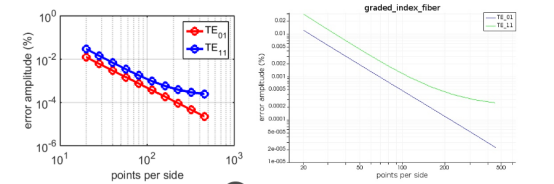
(左图) 模式计算的误差幅度与梯度指数光纤TE模式的解析结果比较，操作波长为1微米。x轴表示计算区域每边的网格点数。(右图)仅使用内置MODE函数生成的相同图形（无Matlab接口）。

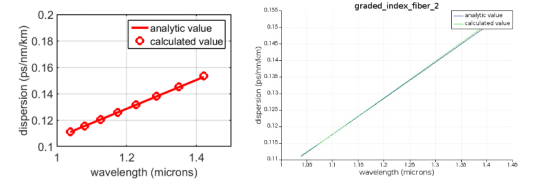
（左）使用MODE（o）计算的渐变指数光纤中TE01模式的分散与解析解（实线）的比较。此计算中使用了每边80个网格点。（右）仅使用内置MODE函数生成的相同图（无Matlab接口）。

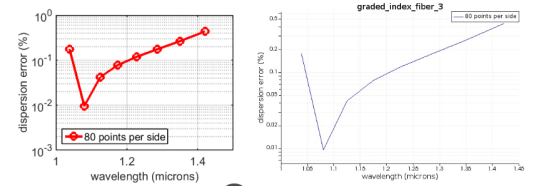
（左）渐变折射率光纤 TE01 模式色散的 MODE 计算误差大小，与解析结果相比。此计算每边使用了 80 个网格点。（右）仅使用内置 MODE 函数（无 Matlab 接口）生成的相同图形。

注意：详细色散设置对色散精度的影响

在频率扫描中禁用了详细色散选项，以计算渐变折射率光纤中 TE01 模式的色散。在这种情况下，频率采样足够精细，能够获得色散的准确结果。实际上，启用详细色散并采用默认的分数波长偏移（0.0001）会导致色散误差增大。其原因在于，在 1 至 1.5 微米的波长范围内，有效折射率的变化非常小，如下图所示。

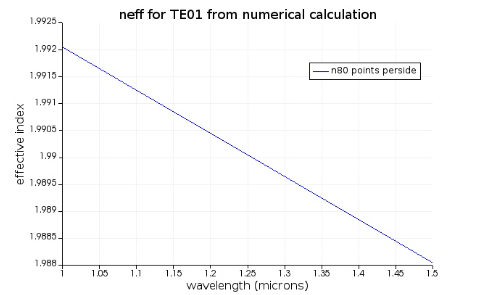
因此，如果用于计算有效折射率导数的频率步长过小，有效折射率的变化可能会与有效折射率计算的精度相当，从而导致导数计算中的数值误差。