leetcode_74 搜索二维矩阵
1. 题意
给你一个满足下述两条属性的 m x n 整数矩阵:
-
每行中的整数从左到右按非严格递增顺序排列。
-
每行的第一个整数大于前一行的最后一个整数。
给你一个整数 target ,如果 target 在矩阵中,返回 true ;
否则,返回 false 。
2. 题解
2.1 暴力
逐个判断即可;
时间复杂度O(mn)O(mn)O(mn)
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {for (auto &M: matrix) {for (auto v: M) {if( v == target)return true;}}return false;}
};
2.2 逐行二分
由于一行的数是有序的,因此可以不用完全遍历。
而且二分查找target。
时间复杂度O(mlogn)O(m \log n)O(mlogn)
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int m = matrix.size();if (0 == m)return false;for (int i = 0;i < m; ++i) {auto it = lower_bound( matrix[i].begin(), matrix[i].end(), target);if ( it != matrix[i].end() && *it == target)return true;}return false;}
};
2.3 整体二分
由于rrr行的最后一个元素是小于r+1r+1r+1行的第一个元素。
我们可以将这个二维数组给看成一个有序的一维数组。
用下标kkk表示原来数组matrix[k/n][k%n]matrix[k/n][k \%n]matrix[k/n][k%n]这个元素,
在[0,mn)[0,mn)[0,mn)这个新下标间进行二分。
时间复杂度O(logmn)=O(logm+logn)O(\log mn) = O(\log m + \log n)O(logmn)=O(logm+logn)
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int m = matrix.size();if (0 == m)return false;int n = matrix[0].size();int l = 0;int r = m * n - 1;while ( l <= r) {int mid = ((r - l) >> 1) + l;int v = matrix[mid / n][mid % n];if ( v == target)return true;if ( v > target)r = mid - 1;else l = mid + 1;}return false;}
};
2.4 两次二分
我们可以二分查找最后一列,找到第一个不小于targettargettarget所在的行。
在对行进行二分,查找最终的targettargettarget值。
时间复杂度O(logm+logn)O(\log m + \log n)O(logm+logn)
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int m = matrix.size();if (0 == m)return false;int n = matrix[0].size();int l;int r;l = 0;r = m;// log mwhile ( l < r) {int mid = ((r - l) >> 1) + l;int v = matrix[mid][n - 1];if ( v == target)return true;if ( v > target)r = mid;elsel = mid + 1;}if ( r >= m )return false;int rows = r;//cout << rows << endl;l = 0;r = n;while ( l < r) {int mid = ((r - l) >> 1) + l;//cout << mid << ": " << matrix[rows][mid] << endl;int v = matrix[rows][mid];if ( v == target)return true;if ( v < target)l = mid + 1;else r = mid;}return false;}
};
2.5 二叉搜索树
这个想法来自三叶姐,宫水三叶。
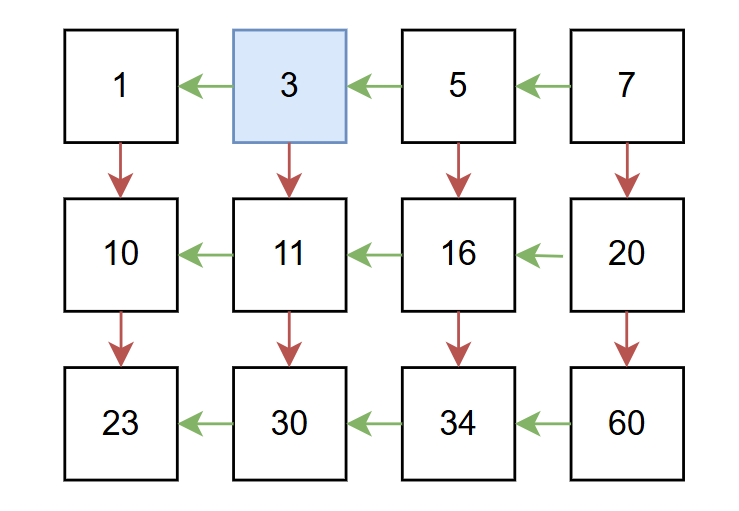
把这样的二维数组想看成以右上角为根节点的二叉搜索树。
当前节点的左边节点必然小于当前节点,
当前节点的下边节点必然大于当前节点。
我们从根开始,如果当前节点大于target,就向左走;
如果当前节点小于target,就向下走。
重复上面的过程,直到超过边界或者找到target。
时间复杂度O(m+n)O(m+n)O(m+n)
class Solution {
public:bool searchMatrix(vector<vector<int>>& matrix, int target) {int m = matrix.size();if (0 == m)return false;int n = matrix[0].size();int x = 0;int y = n - 1;while (x < m && y >= 0) {int v = matrix[x][y];if (v == target)return true;if ( v > target)y--;else x++;}return false;}
};
参考
三叶
leetcode
