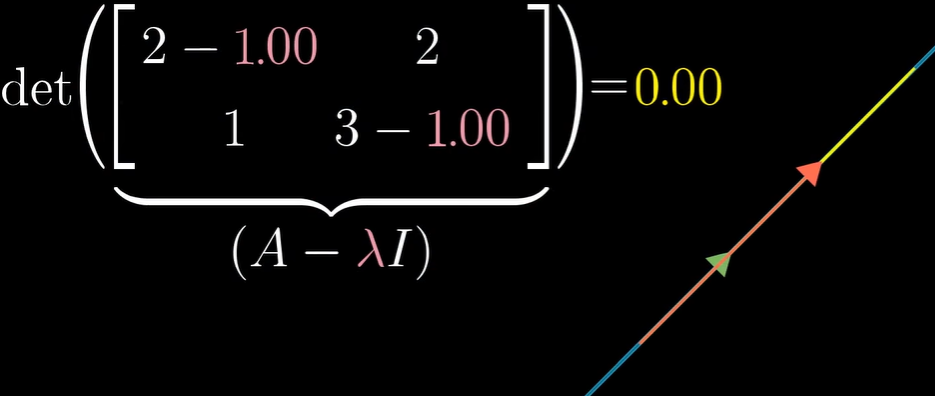秋招 AI 方向 —— 华为机考

2025 年 8 月 27 日 算法岗笔试题的 15 道单选题 + 5 道多选题 + 2 道机器学习编程题。

题目及答案

单选题

1. 下面这段代码执行的功能是什么?

   function forward(x, W, b):logits = Wx+bexp_values = exp(logits)return exp_values / sum(exp_values)
   

   $A$. 全连接层 + $Sigmoid$ 激活

   $B$. 全连接层 + 全局池化操作

   $C$. 全连接层 + $Softmax$ 激活

   $D$. 全连接层 + 均值池化操作

   答案：$C$，实现的是全连接（线性变换）之后接 $Softmax$ 激活，把 $logits$ 转成一组概率。

2. $Transformer$ 中位置编码的主要作用是？

   $A$. 归一化输入

   $B$. 引入序列顺序信息

   $C$. 增加非线性

   $D$. 减少计算量

   答案：$B$，自注意力不含位置信息，位置编码用于给模型注入序列顺序。

3. 线性方程组 $4x+y=6x+3y=3$ 初始解 $(x_0,y_0)=(0,0)$，进行一次 $Javobi$ 迭代后，$(x_1,y_1)$ 是：

   $A$. $(0,0)$

   $B$. $(2,0.5)$

   $C$. $(1,1)$

   $D$. $(1.5,1)$

   答案：$D$，详见下文 Jacobi 迭代

4. 关于大模型的"幻觉”（$Hallucination$）现象，下列说法错误的是

   $A$. 模糊或复杂的提示词输入可能导致幻觉

   $B$. 指模型生成看似合理但与事实不符的内容

   $C$. 增加训练数据的多样性可以完全消除幻觉

   $D$. 检索增强生成技术可缓解幻觉问题

   答案：$C$，训练多样性只能降低但不能“完全消除”幻觉。

5. 已知矩阵 $A$ 是 $3$ 阶不可逆矩阵，${\alpha }_1,{\alpha }_2$是齐次线性方程组 $Ax=0$ 的基础解系，${\alpha }_3$ 是矩阵 $A$ 属于特征值 $\lambda =2$ 的特征向量，则不是矩阵特征向量的是：

   $A$. ${\alpha }_1+2{\alpha }_2$

   $B$. $-5{\alpha }_3$

   $C$. $3{\alpha }_1-4{\alpha }_2$

   $D$. $2{\alpha }_1+{\alpha }_3$

   答案：$D$，详见下文 特征值和特征向量

6. 在 $Kmeans$ 算法（采用欧式距离）中，存在 $4$ 个簇，簇 $C_1$ 的中心为 $[1,1]$，簇 $C_2$ 的中心为 $[1,-1]$，簇 $C_3$ 的中心为 $[-1,-1]$，簇 $C_4$ 的中心为 $[-1,1]$，则样本 $[2,-2]$ 属于：

   $A$. 簇 $C_3$

   $B$. 簇 $C_1$

   $C$. 簇 $C_2$

   $D$. 簇 $C_4$

   答案：$C$，计算到各中心的欧式（平方）距离，到 $C_2$ 的距离为 2， 最小。

7. 矩阵 $A=\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right]$ 的零空间维度是？

   $A$. $1$

   $B$. $2$

   $C$. $0$

   $D$. $3$

   答案：$A$，矩阵 $A$ 的秩为 $rank(A)=2$，第三行与前两行相关，零空间维数为 $3-2=1$。详见下文 矩阵的秩。

8. 对于一个 $n\times n$ 的实对称矩阵 $A$，以下哪个说法是正确的？

   $A$. $A$ 的特征值一定都是实数

   $B$. $A$ 的奇异值一定都是复数

   $C$. $A$ 不能进行 $QR$ 分解

   $D$. $A$ 一定可以进行 $LU$ 分解

   答案：$A$，详见下文 实对称矩阵、LU 分解和 QR 分解。

9. 关于奇异值分解（$SVD$），以下说法错误的是：

   $A$. 奇异值矩阵 $\sum$ 的对角元素非负且按降序排列

   $B$. $SVD$ 适用于任意 $m\times n$ 矩阵

   $C$. 左奇异向量是 $A{A}^T$ 的特征向量

   $D$. $SVD$ 唯一确定，即分解结果 $U,\sum ,V$ 唯一

   答案：$D$，详见下文 SVD 分解

10. 若某项目有 $n$ 位选手，每两人之间都要进行一次对战（即总共进行 $\left(\genfrac{}{}{0ex}{}{n}{2}\right)$ 场比赛），最终按胜场数排名，胜场数最高的前 $m$ 人晋级决赛，第 $m$ 名若出现胜场数并列，则需进行加赛，因此不能保证晋级。请问，一个选手最少需要赢几场才能确保晋级？$\lceil \ast \rceil$ 表示向上取整

    $A$. $\lceil \frac{(2n-m-1)}{2}\rceil$

    $B$. $\lceil \frac{(m-1)}{2}\rceil$

    $C$. $\lceil \frac{(m-1)+(n-1)+1}{m-n+1}\rceil$

    $D$. $\lceil \frac{(m-1)n}{m}\rceil$

    答案：$D$。晋级需确保胜场数大于剩余 $n-m$ 人可能胜场，公式推导得 $\lceil \frac{(m-1)n}{m}\rceil$。

11. 任何一个连续型随机变量的概率密度中 $\varphi (x)$ 一定满足

    $A$. 在定义域内单调不减

    $B$. $\varphi (x)\ge 1$

    $C$. $0\le \varphi (x)\le 1$

    $D$. ${\int }_{-\infty }^{+\infty }\varphi (x)dx=1$

    答案：$D$。概率密度函数要求非负且积分为 1。

12. 在支持向量机（$SVM$）中，假设你正在处理一个非线性可分的数据集，并选择了径向基函数（$RBF$）作为核函数。如果调整参数 $C$ （正则化参数）和 $\gamma$ （核系数）的值，以下哪一项最准确地描述了这两个参数对模型复杂度和泛化能力的影响？

    $A$. 减小 $C$ 增加正则化强度，使模型更简单；减小 $\gamma$ 使决策边界更加平滑，但可能导致欠拟合

    $B$. 减小 $C$ 减少正则化强度，使模型更复杂；减小 $\gamma$ 使决策边界更加灵活，但可能导致过拟合

    $C$. 增大 $C$ 减少正则化强度，使模型更复杂；增大 $\gamma$ 使决策边界更加灵活，但可能导致过拟合

    $D$. 增大 $C$ 增加正则化强度，使模型更简单；增大 $\gamma$ 使决策边界更加平滑，但可能导致欠拟合

    答案：$C$，增大 $C$ $\to$ 减弱正则 $\to$ 模型更复杂；增大 $\gamma$ $\to$ 边界更灵活；均增加过拟合风险。详见 支持向量机

13. $Tokenizer$ 的核心作用是什么?

    $A$. 把文本翻译成中文

    $B$. 把文本变成浮点向量

    $C$. 把文本翻译成英文

    $D$. 把文本变成整数序列

    答案：$D$。

14. 设 $A$、$B$ 为随机事件，且 $P(A)=0.5$，$P(B)=0.6$，$P(B|A)=0.8$，则 $P(B\cup A)=$

    $A$. $0.7$

    $B$. $1.1$

    $C$. $0.3$

    $D$. $0.8$

    答案：$A$。容斥原理（加法规则），基本公式为：$P(B\cup A)=P(A)+P(B)-P(A\cap B)$，又由条件概率，$P(A\cap B)=P(B|A)P(A)$，可得 $0.5+0.6-0.8\cdot 0.5=0.7$。

15. 设总体 $X$ 的概率分布为 $P(X=1)=\frac{1-\theta }{2}$，$P(X=2)=P(X=3)=\frac{1+\theta }{4}$，利用来自总体的样本值 $2,2,1,3,1,3,1,2$，可得 $\theta$ 的最大似然估计值为

    $A$. $1/2$

    $B$. $3/5$

    $C$. $1/4$

    $D$. $2/5$

    答案：$C$。

多选题

16. 对线性方程组：$\{\begin{array}{l}5x+y=2\\ x+3y=4\end{array}$ 使用高斯-赛德尔迭代法，初始值 $(x^{(0)},y^{(0)})=(0,0)$。下列结果正确的是？

    $A$. 经过两步迭代：$x^{(2)}=0.08,y^{(2)}=1.28$

    $B$. $x^{(1)}=0.4$

    $C$. 迭代矩阵的谱半径 $\rho (B_{Gs})>1$，方法发散

    $D$. $y^{(1)}=1.2$

    答案：$B$、$D$，详见下文 Gauss–Seidel 迭代

17. 你想使用朴素贝叶斯分类器来过滤垃圾邮件。该模型的核心是贝叶斯公式 $P(\text{class}|\text{features})\propto P(\text{features}|\text{class})\ast P(\text{class})$。为了让这个模型有效工作，你需要从训练数据中估计哪些概率值?

    $A$.在给定类别下，每个特征(例如，每个单词)出现的条件概率 $P(单词|类别)$。

    $B$. 每个类别的先验概率 $P(类别)$，例如 $P(垃圾邮件)$ 和 $P(正常邮件)$。

    $C$. 特征之间的联合概率 $P(单词1,单词2|类别)$。

    $D$. 每个特征的边缘概率 $P(单词)$。

    答案：$A$、$B$，详见下文 朴素贝叶斯

18. 在卷积神经网络（CNN）中，以下操作属于线性变换的是：

    $A$. 卷积操作

    $B$. 激活函数 $ReLU$

    $C$. 全连接层

    $D$. 池化操作

    答案：$A$、$C$，激活函数本来就是为了引入非线性的，最大池化显然也是非线性的。详见下文 卷积、池化、全连接层和激活函数

19. 下面关于决策树、$XGBoost$ 算法的说法，正确的有？

    $A$. $XGBoost$ 不支持正则化机制，无法控制树的复杂度，因此在高维稀疏数据上容易过拟合。

    $B$. 决策树通过最小化节点不纯度进行分裂，因此深度越大，训练误差越小，模型泛化性能也越好。

    $C$. $XGBoost$ 在每轮迭代中对损失函数进行二阶泰勒展开，利用梯度和 $Hessian$ 信息构建新弱学习器，提升收敛速度与预测精度。

    $D$. 基尼不纯度用于衡量节点中样本的类别纯度，其值越大表示样本类别越混杂，常用于分类树的分裂标准。

    答案：$C$、$D$，详见下文 XGBoost 算法

20. 一位工程师正在为一个包含大量专业术语（如医疗、法律文书）的知识库构建一个 $RAG$（检索增强生成）系统。在设计和调试文本处理与检索流程时，他得出了一系列结论。请判断下列结论中，哪些是准确的?

    $A$. 一个标准的 $RAG$ 系统在处理用户请求时，其信息流是：先将用户的文本查询转换为一个查询向量，用此向量在数据库中检索出最相似的若干个文档块的向量，然后将这些文档块的原始文本（而非它们的向量）与原始查询一同作为上下文，提供给大语言模型（$LLM$）生成最终答案。

    $B$. 在进行文档切分（$Chunking$）时，选择一个极小的、固定的切分尺寸（如 $32$ 个 $token$）是最佳策略，因为它能最大化每个文本块（$chunk$）的语义集中度，从而确保向量检索的精准性。

    $C$. 使用一个在通用网络文本上预训练的 $Tokenizer$ 处理这些专业文档时，许多专业术语会被切分成多个通用子词（$sub-word$）。这种切分会“稀释"原术语的特定义，可能导致其生成的 $Embedding$ 向量质量下降。

    $D$. 为了优化线上服务的推理速度和成本，可以采用一个强大的重量级模型来离线处理所有文档并生 $Embedding$，同时在线上使用一个轻量级模型来实时编码用户的查询（$Query$），只要这两个模型都属于同一系列（如都是 $BERT$ 的变体）即可。

    答案：$A$、$C$。
    $A$ 正确：$RAG$ 流程为查询向量化检索文本后送 $LLM$；$C$ 正确：通用 $tokenizer$ 切分专业术语会稀释语义；$B$ 错误：块过小破坏上下文；$D$ 错误：离线在线模型需一致确保向量空间对齐。详见 检索增强生成：RAG

机器学习编程题

1. 标签样本数量

【题目内容】

$KNN$ 算法的核心思想是，如果一个样本在特征空间中的 $K$ 个最相邻的样本中的大多数属于某一个类别，则该样本也属于这个类别，并具有这个类别上样本的特性。请按照下面的步理，实现 $KNN$ 算法。

$KNN$ 算法说明：

计算待分类点到其他样本点的距离；

通过距离进行排序，选择距离最小的 $K$ 个点；提取这 $K$ 个临近点的类别，根据少数服从多数的原则，将 占比最多的那个标签 赋值给 待分类样本点的 $label$。

本题说明：

1、给定数据集中，默认每一类标签都存在数据，不存在某类型数量为 $0$ 的场景；

2、为消除不同特征权重问题，给出数据均已做好归一化处理，并保留两位小数；

3、出现并列第一的情形时，取并列第一的样本中，最近邻居的标签返回；

4、距离函数定义为：$d_{x,y}=\sqrt{{\sum }_{i=1}^n(x_i-y_i{)}^2}$。

【输入描述】

第 $1$ 行：$kmns$ ：$k$ 代表每次计算时选取的最近邻居个数（不大于 $20$ ），$m$ 代表样本数量（不大于 $200$ ），$n$ 代表样本维度（不包括标签，不大于 $5$ ），$s$ 代表类别个数（不于 $5$）；

第 $2$ 行：待分类样本。

第 $3$ 行 ~ 第 $m+2$ 行：$m$ 个样本，每一行 $n+1$ 列，最后一列为类别标签 $label$。

【输出描述】

输出待分类样本的类别标签及距离最小的 $K$ 个点中的该标签样本数量。

【样例1】

输入：

3 10 2 3
0.81 0.64
0.19 0.2 1.0
0.18 0.14 0.0
0.76 0.58 1.0
0.4 0.16 1.0
0.98 0.85 0.0
0.42 0.97 1.0
0.75 0.26 1.0
0.24 0.06 1.0
0.97 0.8 0.0
0.21 0.1 2.0

输出：

0 2

【说明】

第 $1$ 行输入说明输入了 $m=10$ 个样本，每个样本有 $n=2$ 个维度的数据（去除最后一列标签），共有 $s=3$ 种类别；

第 $2$ 行输入待分类样本的 $n$ 维数据；

从第 $3$ 行到第 $12$ 行的前两列数据为输入的 $m=10$ 个样本，每个样本有 $n=2$ 个维度的数据 + 最后一列的标签数据；

待分类样本 $[0.81,0.64]$ 最近的前 $k=3$ 个邻居分别为：$[0.76,0.58],[0.98,0.85],[0.97,.08]$，分别有 $2$ 个 $0$ 号标签和 $1$ 个 $1$ 号标签，$0$ 号标签占多，返回 $0$ 以及标签 $0$ 的样本数量 $2$。

【样例2】

输入：

6 10 2 4
0.78 0.63
0.57 0.07 1.0
0.5 0.13 1.0
0.83 0.07 3.0
0.27 0.87 3.0
0.81 0.44 2.0
0.21 0.73 3.0
0.45 0.91 1.0
0.12 0.22 2.0
0.25 0.48 0.0
0.54 0.87 1.0

输出：

1 2

【说明】

本样例的距离最小的 $6$ 个样本中，标签 $1$ 和标签 $3$ 出现次数都是 $2$ 次，并列第一；虽然 $[0.8,0.44]$ 距离样本最近，但其标签 $2$ 不是出现最多的，排除在下一轮统计样本中此时需要从标签 $1$ 和标签 $3$ 中的样本中，选取距离最近的 $[0.54,0.87]$ 的标签 $1$ 作为返回值，并同时返回标签 $1$ 的样本数量 $2$。

【解题思路】

2. F1 值最优的决策树剪枝

知识点

线性代数

特征值和特征向量

3Blue1Brown 特征向量与特征值

比如下面这个 二维空间中的线性变换，把 $i$ 基向量变换到 $(3,0)$，把 $j$ 基向量变换到 $(1,2)$，如果用矩阵来表示该线性变换，它的列就是这两个变换后的基向量，

大部分向量在变换中都离开了 其张成的空间，即该向量所在的直线，不过 某些向量在变换中的确留在了其张成的空间，意味着 矩阵对它的作用仅仅是拉伸或压缩而已，如同一个标量。

例如，$i$ 基向量变成了原来的 3 倍，仍留在 $x$ 轴上，$x$ 轴上的任何其他向量都只是被拉伸为原来的 3 倍；还有一个 $(-1,1)$，它在变换中也留在自己张成的空间里，最终被拉伸为 2 倍。

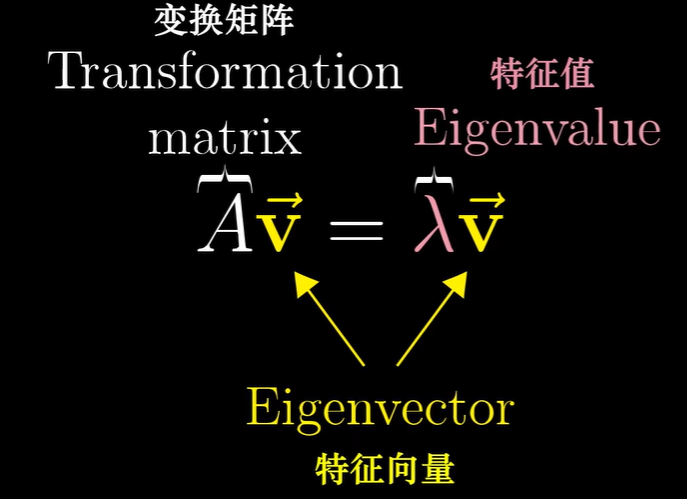
这些特殊向量（留在它们张成的空间），就被称为变换的 特征向量，每个特征向量对应的其在变换中拉伸或压缩比例的值，叫做该特征向量的 特征值。

考虑一个 三维空间中的旋转，如果你能找到这个旋转的 特征向量，也就是留在它张成的空间里的向量，那么你找到的就是 旋转轴。

当且仅当 矩阵所代表的变换将空间压缩到更低的维度时，才会存在一个非零向量，使得矩阵和它的乘积为零向量，而 空间压缩对应的就是矩阵的行列式为零。

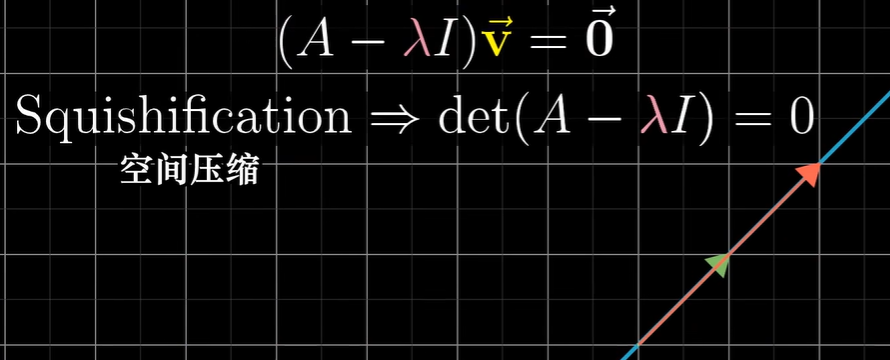
• 同一特征值对应的特征向量 的 任意非零线性组合 仍然是 该特征值的特征向量（构成该特征值的特征子空间）。
• 不同特征值对应的特征向量 之间一般 线性无关，且它们的 非平凡线性组合通常不是特征向量（除非组合恰好退化成某一特征子空间内的向量）。

本题中，已知 ${\alpha }_1,{\alpha }_2$ 是齐次方程 $Ax=0$ 的基础解系，说明 $A{\alpha }_1=0,A{\alpha }_2=0$。所以 ${\alpha }_1,{\alpha }_2$ 都是对应特征值 $\lambda =0$ 的特征向量，且任意非零线性组合（例如 ${\alpha }_1+2{\alpha }_2$、$3{\alpha }_1-4{\alpha }_2$）仍然是特征值 0 的特征向量。

已知 ${\alpha }_3$ 是对应特征值 $\lambda =2$ 的特征向量，所以任意非零标量倍数（例如 $-5{\alpha }_3$）仍是特征向量。

检查 $D$：$v=2{\alpha }_1+{\alpha }_3$。$Av=2A{\alpha }_1+A{\alpha }_3=2\cdot 0+2{\alpha }_3=2{\alpha }_3.$ 若 $v$ 是某个特征值 $\theta$ 对应的特征向量，则需满足 $Av=\theta v=\theta (2{\alpha }_1+{\alpha }_3)$。比较两边得到
$$2{\alpha }_3=2\theta {\alpha }_1+\theta {\alpha }_3.$$

由于 ${\alpha }_1$（属于 eigenspace $\lambda =0$）与 ${\alpha }_3$（属于 eigenspace $\lambda =2$）是线性无关的（不同特征值对应的特征向量线性无关），上式在 ${\alpha }_1,{\alpha }_3$ 基下等价于两个标量方程：
$$2\theta =0,\theta =2,$$

不可能同时成立。因此 $2{\alpha }_1+{\alpha }_3$ 不是任何特征值的特征向量（除非它是零向量，但明显不是）。

特征值 VS 奇异值

• 特征值 / 特征向量（eigen）：告诉有没有 固定方向（不改变方向、只被缩放或反向）的向量，以及对应的缩放因子 $\lambda$。适合分析 把某些方向保持不变的变换（尤其对称矩阵很有用）。

  特征值 / 特征向量（$Av=\lambda v$）

  • 含义：存在方向 $v$（称特征向量），作用 $A$ 后只把 $v$ 缩放（或反向）为 $\lambda v$。
  • 特征值可以为负或复数（例如 旋转的特征值是复数 $\cos \theta \pm i\sin \theta$），不一定非负。

• 奇异值 / 奇异向量（singular）：告诉任意线性变换把 单位球 变成 椭球 时，椭球的半轴长度（非负），以及这些轴在输入/输出空间的方向。奇异值总是非负实数，对任意矩阵都存在。

  奇异值 / 奇异向量（SVD 的语境）

  • 定义：奇异值 ${\sigma }_i$ 是 矩阵 $A^{T}A$ 的非负特征值的平方根：
    $${\sigma }_i=\sqrt{{\text{eigenvalue}}_i(A^{T}A)}.$$
    对应的右奇异向量 $v_i$ 是 $A^{T}A$ 的特征向量，左奇异向量 $u_i$ 是 $A{A}^T$ 的特征向量。
  • 存在性：对任意矩阵（方阵或非方阵、可逆或不可逆）都存在 SVD，因此 奇异值总有定义且为非负实数。
  • 几何意义（最重要的直观）：把单位球 {x:∥x∥=1}\{x:\|x\|=1\}{x:∥x∥=1} 在变换 $A$ 下映成一个椭球。这个椭球的 半轴长度 就是奇异值 ${\sigma }_1\ge {\sigma }_2\ge \cdots$。
    • $V$ 的列（右奇异向量）给出输入空间中被映为这些半轴方向的原始方向；
    • $U$ 的列（左奇异向量）给出输出空间中椭球半轴的方向；
    • $\Sigma$ 的对角元就是相应的伸缩长度（奇异值）。
  • 性质：奇异值非负；按大小排序，最大奇异值等于算子范数（spectral norm，最大放大倍数）。如果最小奇异值为 0，说明矩阵欠秩（不可逆）。

几何图像：

• 特征值/向量 = “哪条直线被直接拉长/缩短 不改变方向”；
• 奇异值/向量 = “把单位圆（球）变成椭圆（椭球）：奇异值是半轴长度，左右两个正交方向分别是输入与输出的主方向”。

矩阵的秩

3Blue1Brown 逆矩阵、列空间与零空间
当变换的结果是一条直线时，也就是说结果是一维的，称这个 变换的秩 为 1；如果变换后的向量落在一个二维平面上，称这个 变换的秩 为 2，所以说，秩 代表 变换后空间的维数。

如果一个三维变换的行列式为零，并且 变换结果仍旧充满整个三维空间，那么它的秩为 3。

矩阵的列告诉了基向量变换后的位置，这些 变换后的基向量张成的空间 就是所有可能的变换结果，换句话说，列空间就是矩阵的列所张成的空间。所以秩的更精确的定义是列空间（或行空间）的维数，表示列向量（或行向量）中 线性无关向量的最大个数。

当秩达到最大值时，意味着秩与列数相等，称之为 “满秩”。注意，零向量一定被包含在列空间中，因为线性变换必须保持原点位置不变。
对一个满秩变换来说，唯一能在变换后落在原点的就是零向量自身，但对一个 非满秩的矩阵 来说，它 将空间压缩到一个更低的维度上。

矩阵 $A=\left[\begin{array}{ccc}1& 2& 3\\ 4& 5& 6\\ 7& 8& 9\end{array}\right]$，对其做 初等行变换 到 行最简阶梯形：

1. $R_2\leftarrow R_2-4R_1$， $R_3\leftarrow R_3-7R_1$：
   $$\left[\begin{array}{ccc}1& 2& 3\\ 0& -3& -6\\ 0& -6& -12\end{array}\right].$$
2. $R_3\leftarrow R_3-2R_2$：
   $$\left[\begin{array}{ccc}1& 2& 3\\ 0& -3& -6\\ 0& 0& 0\end{array}\right].$$
3. 将第2行除以 $-3$：$R_2\leftarrow R_2/(-3)$，得到
   $$\left[\begin{array}{ccc}1& 2& 3\\ 0& 1& 2\\ 0& 0& 0\end{array}\right].$$
4. 用第2行消去第1行的第2列：$R_1\leftarrow R_1-2R_2$，得到行最简阶梯形
   $$\left[\begin{array}{ccc}1& 0& -1\\ 0& 1& 2\\ 0& 0& 0\end{array}\right].$$

从上面的行简化结果可以看出 主元（pivot）在第 1 列和第 2 列，共 2 个，所以矩阵的秩 $\mathrm{rank}(A)=2$。

矩阵是 $3\times 3$，由 秩-零空间维数定理（Rank–Nullity）：$$\text{rank}(A)+\text{nullity}(A)=n=3.$$

因此零空间（nullspace）的维度为 $\text{nullity}(A)=3-2=1.$

可以顺便写出零空间的一个基：设 $x=[x_1,x_2,x_3{]}^T$ 满足 $Ax=0$。由行约简得到方程组
$$x_1-x_3=0,x_2+2x_3=0.$$
令自由变量 $x_3=t$，得到 $$x=t\left[\begin{array}{c}1\\ -2\\ 1\end{array}\right].$$ 所以零空间是一维，基向量可取 $[1,-2,1{]}^T$。

• 若 $\text{rank}(A)=n$（方阵满秩），则 $A$ 可逆（$\det (A)\ne 0$）；否则不可逆（本题 $\det A=0$）。
• 线性方程组 $Ax=b$ 可解性的判定与秩有关：若 $\mathrm{rank}(A)=\mathrm{rank}([A|b])$ 则有解；否则无解。解的自由度（自由变量个数）等于 $n-\mathrm{rank}(A)$。

线性方程组的迭代解法（Jacobi）

Jacobi 迭代的思想：把 每个未知量用“其他未知量”的旧值表示 出来，然后 并行更新所有未知量。

对于第 $i$ 个未知量 $x_i$，要得到一个 显式的更新公式
$$x_i^{(k+1)}=\text{(常数)}+\sum _{j\ne i}\text{(系数)}\cdot x_j^{(k)}$$
为了得到这样的显式公式，必须把第 $i$ 个方程 整理成“关于 $x_i$ 的等式”（即把 $x_i$ 单独放左边，右边只含常数和其他变量）。

本题中，第一个方程要写成 $x=\cdots$，第二个写成 $y=\cdots$。方程组是
$$\{\begin{array}{l}4x+y=6,\\ x+3y=3.\end{array}$$

对第一个方程“解出 $x$”，对第二个方程“解出 $y$”得到
$$x=\frac{6-y}{4},y=\frac{3-x}{3}$$

这就是 Jacobi 的 更新公式：
$$x^{(k+1)}=\frac{6-y^{(k)}}{4},y^{(k+1)}=\frac{3-x^{(k)}}{3}.$$

注意 右边都用到的是上一轮的 $x^{(k)},y^{(k)}$。这正是 Jacobi 并行更新的要点。

矩阵/通用形式：设 $A\mathbf{x}=\mathbf{b}$。把 $A$ 分解为对角 $D$、严格下三角 $L$、严格上三角 $U$：$A=D+L+U$。Jacobi 迭代写成
$${\mathbf{x}}^{(k+1)}=D^{-1}(\mathbf{b}-(L+U){\mathbf{x}}^{(k)}).$$
这也说明：每一步要用 $D^{-1}$（即把对角元素取倒数）去“解出”每个分量 $x_i$，因此每个方程都被整理为“关于自身未知量”的显式表达式。
前提条件：对角元素不能为 0（否则无法求 $D^{-1}$）；收敛性通常还需要一定条件（例如严格对角占优或谱半径 < 1）。

给定初始解 $(x^{(0)},y^{(0)})=(0,0)$，代入得到一次迭代的值：

• $x^{(1)}=\frac{6-y^{(0)}}{4}=\frac{6-0}{4}=\frac{6}{4}=\mathrm{1.5.}$
• $y^{(1)}=\frac{3-x^{(0)}}{3}=\frac{3-0}{3}=1.$

所以 $(x_1,y_1)=(1.5,1)$。

补充：与 Gauss–Seidel 的区别

• Jacobi：计算 $x^{(k+1)}$ 和 $y^{(k+1)}$ 时都只用上一次的值 $x^{(k)},y^{(k)}$（并行更新）。
• Gauss–Seidel：先用上一次值算出 $x^{(k+1)}$，再马上用这个新的 $x^{(k+1)}$ 去算 $y^{(k+1)}$（顺序更新）。

在本例，如果用 Gauss–Seidel，从 $(0,0)$ 一次迭代会得到 $x^{(1)}=1.5$，然后 $y^{(1)}=(3-1.5)/3=0.5$，结果为 $(1.5,0.5)$。

Jacobi 有用 因为它 简单、并行友好且对稀疏问题天然适配，虽然单独用时可能慢，但它是构造更复杂高效方法（如 multigrid、预条件 Krylov 方法）里的重要模块。

• 求解 大型稀疏线性方程组 $A\mathbf{x}=b$，尤其是来自 偏微分方程（PDE）离散化 的问题（如 Poisson、热传导、流体动力学等）。这些问题 矩阵很大、稀疏，直接解（LU）成本高且内存占用大，迭代法更合适。

• 并行 / 分布式计算场景：Jacobi 的并行化开销小，适合在多核/多机上实现。

线性方程组的迭代解法（Gauss–Seidel）

考察点：需要会写 Gauss–Seidel 的逐分量更新公式、做几步迭代，并能判断迭代矩阵的谱半径或用对角占优等充分条件判断收敛性。

1. 写出 Gauss–Seidel 的更新公式（按行顺序代入最新值）：
   $$\{\begin{array}{l}{x}^{(k+1)}=\frac{2-y^{(k)}}{5},\\ y^{(k+1)}=\frac{4-x^{(k+1)}}{3}.\end{array}$$

2. 从 $(x^{(0)},y^{(0)})=(0,0)$ 进行迭代：

   • 第一步：
     $$x^{(1)}=\frac{2-0}{5}=0.4,y^{(1)}=\frac{4-0.4}{3}=\frac{3.6}{3}=\mathrm{1.2.}$$

     所以 $x^{(1)}=0.4$（$B$ 正确），$y^{(1)}=1.2$（$D$ 正确）。

   • 第二步：
     $$x^{(2)}=\frac{2-y^{(1)}}{5}=\frac{2-1.2}{5}=\frac{0.8}{5}=0.16,$$

     $$y^{(2)}=\frac{4-x^{(2)}}{3}=\frac{4-0.16}{3}=\mathrm{1.28.}$$

     因此 $A$ 中的 $x^{(2)}=0.08$ 是错误的。

3. 收敛性（谱半径）判断：令 $A=\left(\begin{array}{cc}5& 1\\ 1& 3\end{array}\right)$。Gauss–Seidel 的迭代矩阵是
   $$B_{Gs}=-(D+L{)}^{-1}U$$

   对本例可计算出（或注意到是上三角形式）
   $$B_{Gs}=\left(\begin{array}{cc}0& -\frac{1}{5}\\ 0& \frac{1}{15}\end{array}\right),$$

   特征值为 $0$ 和 $1/15$，所以谱半径 $\rho (B_{Gs})=1/15<1$。因此迭代收敛，选项 C（$\rho >1$）错误。

   （另外也可用充分条件判断：矩阵对角占优，故 Gauss–Seidel 收敛。）

关于迭代矩阵，更具体的求解过程如下：

1. 矩阵分解 $A=D+L+U$
   把矩阵 $A=\left(\begin{array}{cc}5& 1\\ 1& 3\end{array}\right)$ 分成 对角、严格下三角和严格上三角 三部分：
   $$D=\left(\begin{array}{cc}5& 0\\ 0& 3\end{array}\right),L=\left(\begin{array}{cc}0& 0\\ 1& 0\end{array}\right),U=\left(\begin{array}{cc}0& 1\\ 0& 0\end{array}\right).$$
   Gauss–Seidel 的逐分量更新可写成矩阵形式
   $$(D+L)x^{(k+1)}=-U{x}^{(k)}+b,$$
   移项得到
   $$x^{(k+1)}=-(D+L{)}^{-1}U{x}^{(k)}+(D+L{)}^{-1}b.$$
   因此迭代矩阵就是
   $$B_{Gs}=-(D+L{)}^{-1}U.$$
2. 计算 $(D+L{)}^{-1}$ 与 $B_{Gs}$
   先写出 $D+L$：
   $$D+L=\left(\begin{array}{cc}5& 0\\ 1& 3\end{array}\right).$$
   计算 $D+L$ 矩阵的逆：$$\left(\begin{array}{cc}5& 0\\ 1& 3\end{array}\right)\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)=\left(\begin{array}{cc}1& 0\\ 1& 3\end{array}\right)\left(\begin{array}{cc}\frac{1}{5}& 0\\ 0& 1\end{array}\right)=\left(\begin{array}{cc}1& 0\\ 0& 3\end{array}\right)\left(\begin{array}{cc}\frac{1}{5}& 0\\ -\frac{1}{5}& 1\end{array}\right)=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)\left(\begin{array}{cc}\frac{1}{5}& 0\\ -\frac{1}{15}& \frac{1}{3}\end{array}\right)$$
   $$B_{Gs}=-(D+L{)}^{-1}U=\left(\begin{array}{cc}0& -\frac{1}{5}\\ 0& \frac{1}{15}\end{array}\right).$$
3. 求特征值（谱半径）
   注意这个 $B_{Gs}$ 是上三角矩阵（非零条目在对角线上和右上角），所以它的特征值就是对角线元素：
   $${\lambda }_1=0,{\lambda }_2=\frac{1}{15}.$$
   谱半径 是 特征值绝对值的最大值：
   $$\rho (B_{Gs})=\max (|0|,|1/15|)=\frac{1}{15}<1.$$
   结论：谱半径小于 1，Gauss–Seidel 方法对本例收敛。

LU 分解和 QR 分解

分解	形式	是否总存在	应用
LU	$PA=LU$	不一定（必须允许行交换）	解线性方程组（快速求解）
QR	$A=QR$	对任意矩阵都存在	最小二乘问题，数值稳定计算

LU 分解（Lower–Upper Decomposition）：把一个矩阵 $A$ 分解成 下三角矩阵 $L$ 和 上三角矩阵 $U$ 的乘积：
$$A=LU$$

有时为了保证分解存在，需要引入置换矩阵 $P$：

$$PA=LU$$

这叫 带主元的 LU 分解。

LU 分解其实就是把 高斯消元 的过程“打包”成一个分解：

• 消元得到的系数记录在 $L$ 里；
• 最后得到的上三角结果就是 $U$。

好处：解线性方程组 $Ax=b$ 时，不用每次都重新消元，可以用分解快速解：
$$Ax=b\Rightarrow LUx=b\Rightarrow Ly=b\Rightarrow Ux=y$$
两次三角方程求解即可（代价低很多）。

例如，$$A=\left[\begin{array}{cc}2& 3\\ 4& 7\end{array}\right]$$
做消元：用第 1 行消去第 2 行，系数是 $4/2=2$。于是：
$$L=\left[\begin{array}{cc}1& 0\\ 2& 1\end{array}\right],U=\left[\begin{array}{cc}2& 3\\ 0& 1\end{array}\right]$$

QR 分解（Orthogonal–Upper Triangular Decomposition）：把一个矩阵 $A$ 分解为，
$$A=QR$$
$Q$：正交矩阵（列向量正交且单位化，满足 $Q^{\top }Q=I$），$R$：上三角矩阵。

适用于任意矩阵（方阵/矩阵都可以）。

QR 分解本质上是 对列向量做 Gram–Schmidt 正交化：

• 把 $A$ 的列向量变成一组正交单位向量（放在 $Q$ 中）；
• 正交化过程中得到的投影系数就是 $R$。

在几何意义上，$Q$ 是旋转/反射（不会改变长度和角度），$R$ 则包含缩放、组合的信息。

比如求解超定方程组（最小二乘问题）：
$$\underset{x}{\min }\Vert Ax-b{\Vert }_2$$
用 QR 分解可以变成简单的三角系统求解。数值稳定性比 LU 分解更好，所以在科学计算中很常用。

$$A=\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right]$$
对列向量做 Gram–Schmidt：

• 第 1 列 $[1,1{]}^T$，归一化：$\frac{1}{\sqrt{2}}[1,1{]}^T$。
• 第 2 列 $[1,-1{]}^T$，与第 1 列正交（本来就正交），归一化：$\frac{1}{\sqrt{2}}[1,-1{]}^T$。

于是：
$$Q=\frac{1}{\sqrt{2}}\left[\begin{array}{cc}1& 1\\ 1& -1\end{array}\right],R=\left[\begin{array}{cc}\sqrt{2}& 0\\ 0& \sqrt{2}\end{array}\right]$$

SVD 分解

SVD 写为
$$A=U\Sigma V^{\top },$$

其中 $\Sigma =\mathrm{diag}({\sigma }_1,{\sigma }_2,\dots )$，通常要求 ${\sigma }_1\ge {\sigma }_2\ge \cdots \ge 0$。（约定奇异值矩阵 $\Sigma$ 的对角元素非负且按降序排列，便于比较大小/截断）

• 右奇异向量 $v_i$ 是 $A^{T}A$ 的特征向量，满足
  $$A^{T}A{v}_i={\sigma }_i^2{v}_i.$$
• 左奇异向量 $u_i$ 是 $A{A}^T$ 的特征向量，滿足
  $$A{A}^T{u}_i={\sigma }_i^2{u}_i.$$

也可以从基本 SVD 等式推导：
$$A{v}_i={\sigma }_i{u}_i,A^T{u}_i={\sigma }_i{v}_i.$$
把第二个式子代入第一个得到 $A{A}^T{u}_i={\sigma }_i^2{u}_i$；同样得到 $A^{T}A{v}_i={\sigma }_i^2{v}_i$。

SVD 把任意变换分成“旋转 → 缩放 → 旋转”

任何矩阵 $A$ 都可以写成 $A=U\Sigma V^{\top }$，其中 $U,V$ 正交（旋转/反射），$\Sigma$ 非负对角（缩放）。

• 先用 $V^{\top }$ 把输入坐标系旋转到“奇异向量基”，再用 $\Sigma$ 按坐标轴缩放（这些坐标轴就是椭球主轴），最后 用 $U$ 把结果旋转到输出坐标系。
• 因此 SVD 给了最自然的几何分解：任意线性变换 = 两次正交变换（旋转/反射）夹一个纯拉伸。

例 1：纯缩放 $A=\left(\begin{array}{cc}3& 0\\ 0& 1\end{array}\right)$

• 特征值：3, 1（对应方向 $e_1,e_2$），奇异值同为 3,1（因为 A 是对角且非负）。
• 作用：把单位圆拉成半轴长度 3 与 1 的椭圆，主方向不变。

例 2：纯旋转 $R=R(\theta )$（如 $\theta =90^{\circ }$）

• 特征值：复数（没有实特征向量）
• 奇异值：都等于 1（不改变长度）
• 作用：把单位圆映为同样的单位圆，只改变方向。

例 3：一般矩阵
任何 $A$ 的 SVD $A=U\Sigma V^{\top }$ 说明 $A$ 含有“旋转-拉伸-旋转”成分。如果把一个向量 $x$ 投影在 $V$ 基下，先缩放各分量（由 $\Sigma$ 给出），再用 $U$ 旋转回输出空间。

为什么在实际中常用奇异值（SVD）？

• 总是存在（对任意矩阵），稳定且能处理 非方阵。
• 给出最优低秩近似（Eckart–Young 定理）：截取前 $k$ 个奇异值对应的分解，能得到最佳的秩-$k$ 近似。
• 用于 数值稳定性分析（条件数 $\kappa (A)={\sigma }_{\max }/{\sigma }_{\min }$）。
• 在数据分析（PCA）、图像压缩、最小二乘、伪逆（Moore–Penrose）等都有广泛应用。

线性代数中的常见矩阵类型

1. 对称矩阵 (Symmetric Matrix)：矩阵等于它的转置。
   $$A=A^{\top }$$
   特点是主对角线对称，
   $$\left[\begin{array}{ccc}1& 2& 3\\ 2& 4& 5\\ 3& 5& 6\end{array}\right]$$

2. 实对称矩阵 (Real Symmetric Matrix)：元素全是实数的对称矩阵。特征值一定是实数；可以正交对角化（存在正交矩阵 $Q$，使得 $A=Q\Lambda Q^{\top }$）。

3. 正交矩阵 (Orthogonal Matrix)：列（行）向量两两正交且单位化，不改变向量长度
   $$Q^{\top }Q=I\iff Q^{-1}=Q^{\top }$$
   表示旋转或反射变换，比如二维旋转矩阵：
   $$Q=\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$$

4. 正定矩阵 (Positive Definite Matrix)：对任意非零向量 $x$，
   $$x^{\top }Ax>0$$
   所有特征值都大于 0；常见于协方差矩阵、能量函数等。

5. 半正定矩阵 (Positive Semi-Definite, PSD)：
   $$x^{\top }Ax\ge 0$$
   特征值 $\ge 0$。

6. 对角矩阵 (Diagonal Matrix)：主对角线以外全为 0。
   $$\left[\begin{array}{ccc}1& 0& 0\\ 0& 4& 0\\ 0& 0& 7\end{array}\right]$$

7. 单位矩阵 (Identity Matrix)：对角线全是 1，其余为 0。任何矩阵乘它不变。

8. 零矩阵 (Zero Matrix)：全部元素为 0。

9. 上/下三角矩阵 (Triangular Matrix)：上三角矩阵 的主对角线下方为 0；下三角矩阵 的主对角线上方为 0。

10. 奇异矩阵 (Singular Matrix)：行列式为 0，不可逆。

11. 正交投影矩阵 (Projection Matrix)：把向量投影到某个子空间。
    $$P^2=P$$

12. 幂等矩阵 (Idempotent Matrix)：
    $$A^2=A$$

13. 酉矩阵 (Unitary Matrix)：复数域上的“正交矩阵”，在复数向量空间中保持长度。
    $$U^{\ast }U=I$$

14. 厄米矩阵 (Hermitian Matrix)：复数域上的“对称矩阵”，转置并共轭，特征值一定是实数。
    $$A=A^{\ast }$$

实对称矩阵

把矩阵想成“把向量拉伸/压缩并旋转”的变换。对称矩阵 的特别之处是：它不会把伸长的方向“扭曲成复杂的相位”，它的“伸缩因子”是纯粹的实数（没有复数的“旋转+缩放”混合）。也就是说，对称变换可以被理解为 在一组正交方向上只做实数伸缩。

对称 = “没有复相位”，所以特征值都是实数。

若 $A$ 是实对称的，特征向量可以取正交，且 奇异值等于特征值的绝对值（因为 $A^{T}A=A^2$ 在对称情形下成立，所以 ${\sigma }_i=|{\lambda }_i|$）。

正交矩阵和旋转的关系？

对任意实向量 $u$，其欧几里得范数平方定义为内积自身：$\Vert u{\Vert }^2=u^{T}u.$

正交矩阵 定义：一个 $n\times n$ 的实矩阵 $Q$ 若满足
$$Q^{\top }Q=Q{Q}^{\top }=I_n,$$
就称为 正交矩阵。等价地，$Q^{-1}=Q^{\top }$。

正交矩阵表示 “长度和角度都不变” 的线性变换——本质上是旋转或反射（以及它们的组合）。把向量用 $Q$ 变换后，向量的长度不变，任意两向量之间的内积也不变。

• 正交矩阵 $Q$ 满足 $Q^{\top }Q=I$。因此对任意向量 $x$，$\Vert Qx{\Vert }^2=x^{\top }{Q}^{\top }Qx=x^{\top }x=\Vert x{\Vert }^2$。→ 说明它保持长度，也保持夹角（因为内积不变）。这正是旋转（或反射）应有的性质。

旋转（在欧几里得空间）由 正交矩阵 $Q$ 表示，满足 $Q^{\top }Q=I$ 且 $\det Q=1$（若 $\det =-1$ 则是反射+旋转）。

• 性质：旋转不改变向量长度（$\Vert Qx\Vert =\Vert x\Vert$），所以奇异值全是 1。

• 特征值：二维旋转角度 $\theta$ 的矩阵
  $$R(\theta )=\left(\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right)$$

  的特征值是 $e^{\pm i\theta }=\cos \theta \pm i\sin \theta$ —— 通常是复数，所以没有非零的实特征向量（除非 $\theta =0$ 或 $\pi$）。

几何上：旋转改变方向但不改变长度；特征向量要求“不改变方向”，因此旋转通常 没有实特征向量。

概率论

朴素贝叶斯（Naive Bayes）

参考：Naive Bayes, Clearly Explained 和 Gaussian Naive Bayes, Clearly Explained，Bayes and Naive Bayes Classifier

朴素贝叶斯分类器用的是贝叶斯公式
$$P(\text{class}\mid \text{features})\propto P(\text{features}\mid \text{class})P(\text{class}).$$

• $P(\text{class})$ 是类别先验（例如 $P(\text{spam})$、$P(\text{Normal})$），必须从训练集估计。常用估计：
  $$\hat{P}(\text{class})=\frac{\#\text{train docs in class}}{\#\text{all train docs}}.$$

• 对于 $P(\text{features}\mid \text{class})$，朴素贝叶斯作条件独立假设，把联合条件概率分解为各特征的乘积：
  $$P(\text{features}\mid \text{class})=\prod _{i}P({\text{feature}}_i\mid \text{class}).$$

因此需要估计每个特征（例如每个单词）在该类别下出现的条件概率。常见估计（多项式朴素贝叶斯）：
$$\hat{P}(w|c)=\frac{\text{count}(w\text{ in class }c)+\alpha }{{\sum }_{w^{\prime }}\text{count}(w^{\prime }\text{ in }c)+\alpha V},$$

其中 $\alpha$ 为拉普拉斯平滑参数，$V$ 为词表大小。

为什么联合概率 $P({\text{word}}_1,{\text{word}}_2\mid \text{class})$）不是必须的？

朴素贝叶斯 恰恰是 通过条件独立假设把联合概率拆成各个 $P({\text{word}}_i\mid \text{class})$ 的乘积。 如果你去估计二元或更高阶的联合概率（即放弃独立假设），模型会变得非常复杂、参数爆炸并且需要大量数据（或采用 n-gram、交互特征等替代方法）。但标准朴素贝叶斯不需要直接估计这些高阶联合分布。

为什么边缘概率 $P(\text{word})$ 不是必须的？

在比较不同类别的后验时：
$$P(\text{class}\mid \text{features})=\frac{P(\text{features}\mid \text{class})P(\text{class})}{P(\text{features})}.$$

分母 $P(\text{features})$ 对所有类别相同，因此在做判别（选概率最大的类别）时可以忽略它（只用分子比较）。所以不必单独估计每个特征的边缘概率 $P(\text{word})$。当然，如果想要 真正的归一化后验概率，可以通过
$$P(\text{features})=\sum _{c}P(\text{features}\mid c)P(c)$$

间接算出，但这不是训练时必须单独估计 $P(\text{word})$ 的理由。

• 要避免零概率问题，常用拉普拉斯平滑（$\alpha >0$）。

• 有两种常见特征模型：多项式 NB（考虑词频）和伯努利 NB（考虑词是否出现）。估计公式略有不同，但核心都是估计 $P(\text{word}|class)$ 与 $P(class)$。
• 如果需要捕捉词间依赖，可引入 n-gram 或交互特征，但那就超出“朴素”贝叶斯的假设了。

AI

卷积、池化、全连接层和激活函数

线性算子 的定义是：对任意向量（或函数）$x,y$ 和标量 $a,b$，有

$$T(ax+by)=aT(x)+bT(y).$$

• 卷积满足这个性质：若 $T$ 表示与固定核 $k$ 的卷积，则
  $$T(ax+by)=k\ast (ax+by)=a(k\ast x)+b(k\ast y)=aT(x)+bT(y),$$
  所以卷积是线性变换。

• 全连接层 核心是矩阵乘法 $y=Wx$，这满足线性性（矩阵乘法是线性的）。实际神经网络里常在后面加上偏置 $b$，变为 $y=Wx+b$，这叫仿射变换（affine），严格来说含偏置时不是“线性”而是“仿射”。

  在考试语境中通常把“全连接层”视为线性变换（或把权重部分当作线性）。

• ReLU：$\mathrm{ReLU}(x)=\max (0,x)$。

  检验加法性：$\mathrm{ReLU}(1)=1,\mathrm{ReLU}(-1)=0$，但 $\mathrm{ReLU}(1+(-1))=\mathrm{ReLU}(0)=0$。
  $1+0\ne 0$，因此不满足线性性，ReLU 是非线性（尽管它是分段线性的）。

• 池化：常见的 max pooling 是非线性的（取最大值，不满足加法性），例如 $\max (1,0)=1,\max (-1,0)=0$ 但 $\max (1+(-1),0)=\max (0,0)=0$，不满足线性性。

  注意例外：如果题目中特指 average pooling（均值池化），那是线性的（平均是加权和/矩阵乘法的一种），但一般说“池化”在 CNN 语境中默认是 max pooling，所以视为非线性。

XGBoost 算法

XGBoost = GBDT + 二阶近似 + 正则化 + 工程优化

• Boosting 思想：不是一次性训练一个很强的模型，而是逐步迭代训练很多“弱模型”（如浅树），每次 让新的模型去修正前一轮的误差，最后把它们加起来形成一个强模型。
• XGBoost：是对 梯度提升树（GBDT） 的改进实现，特点是：
  1. 用二阶导数（梯度 + Hessian）提升优化精度；
  2. 加入正则化，控制树的复杂度，防止过拟合；
  3. 利用高效的工程优化（稀疏感知、分块并行、缓存等），速度快。

假设我们要学一个预测函数：

$${\hat{y}}^{(t)}(x)=\sum _{k=1}^t{f}_k(x),f_k\in \mathcal{F}$$

其中每个 $f_k$ 是一棵回归树（叶子节点有一个预测值）。

训练目标函数：
$$\mathcal{L}=\sum _{i}l(y_i,{\hat{y}}_i)+\sum _k\Omega (f_k)$$

• 第一项：损失函数（例如平方误差、逻辑损失等）；
• 第二项：正则化 $\Omega (f)=\gamma T+\frac{1}{2}\lambda {\sum }_j{w}_j^2$，惩罚树叶子数 $T$ 和叶子权重 $w_j$ 的大小，防止过拟合。

在第 $t$ 次迭代时，要加一个新树 $f_t$，但直接最优化很难。XGBoost 的关键 是：对损失函数做 二阶泰勒展开（近似）：
$${\mathcal{L}}^{(t)}\approx \sum _i[g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t(x_i{)}^2]+\Omega (f_t),$$

其中

• $g_i={\partial }_{{\hat{y}}^{(t-1)}}l(y_i,{\hat{y}}_i^{(t-1)})$ （一阶梯度）；
• $h_i={\partial }_{{\hat{y}}^{(t-1)}}^{2}l(y_i,{\hat{y}}_i^{(t-1)})$ （二阶 Hessian）。

这样就把复杂的 损失最小化问题，化简成 只依赖梯度和二阶信息的优化问题。

如何生长一棵树？

• 训练时需要决定：在哪个特征、哪个阈值上分裂。
• XGBoost 定义了一个 分裂增益函数（Gain），衡量分裂前后目标函数下降多少：
  $$Gain=\frac{1}{2}\left[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{(G_L+G_R{)}^2}{H_L+H_R+\lambda }\right]-\gamma$$

其中 $G$、$H$ 是分裂后左右子树上的梯度和 Hessian 总和。

选择 Gain 最大的分裂方式，直到叶子数或深度达到限制。

防止过拟合的机制：

• 正则化项：$\lambda$ 控制叶子权重的平滑，$\gamma$ 控制是否值得新开一个叶子；
• Shrinkage（学习率）：每轮只加一小步，避免过拟合；
• 子采样：随机采样数据行、特征列，减少相关性；
• 树深限制：避免树过深。

工程优化（为什么 XGBoost 特别快）

• 稀疏感知：能自动处理缺失值、稀疏特征；
• 并行化分裂搜索：不同特征的分裂点可以并行搜索；
• Block 结构：数据按列存储，缓存友好；
• 支持分布式训练。