2025年- H101-Lc209--1979.找出数组的最大公约数(gcd最大公约数)--Java版

（一）练习

1.题目描述

2.思路

欧几里得算法
gcd(int a,int b)
{
while(b!=0)//当分母不为0
{
//求余数要先写。
int tmp=a%b;（余数）
a=b;（a移动到b的位置上）
b=tmp;（b就是求出来的余数）
}
return a;//最后返回a
}

举一个例子
12和5的最大公约数是1
（1）tmp=12%5=2；
a=5，b=2
（2）因为b！=0，
tmp=5%2=1；
a=2
b=1
（3）因为b！=0，
tmp=2%1=0
a=1；
b=0；退出循环
此时公约数就是a=1

3.代码实现

import java.util.Arrays;public class solution4 {public int findGCD(int[] nums) {Arrays.sort(nums);//升序排序int min=nums[0];int max=nums[nums.length-1];int res=gcd(min,max);return res;}public static int gcd(int a,int b){while(b!=0){int tmp=a%b;a=b;b=tmp;}return a;}public static void main(String[] args){solution4 test=new solution4();int[] nums={2,5,6,9,10};System.out.println(test.findGCD(nums));}
}

（二）实战（M）
有理数p/q在k进制是否是有限小数。
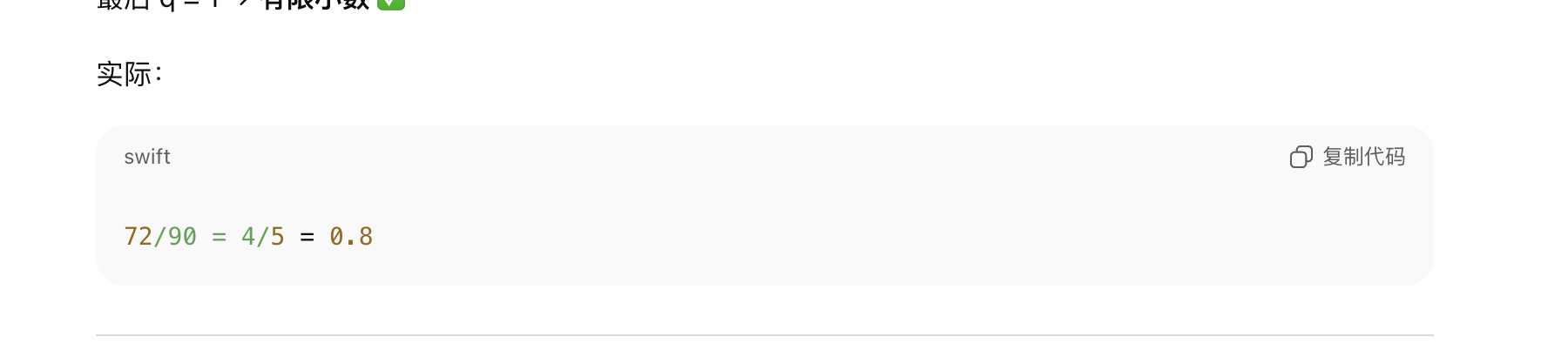
1/2=0.5是有限小数，1/2=0.3333…不是有限小数。
输入：第一行是整数t，代表测试数据的组数
接下来t行，输入三个整数，p（分子），q是（分母），k（进制基数）。
如果p/q在k进制数有限小数，输出“yes”，否则输出“no”
Input：
3
1 2 10
1 3 10
3 4 2
output：
yes
no
yes

思路：判断是否是有限小数
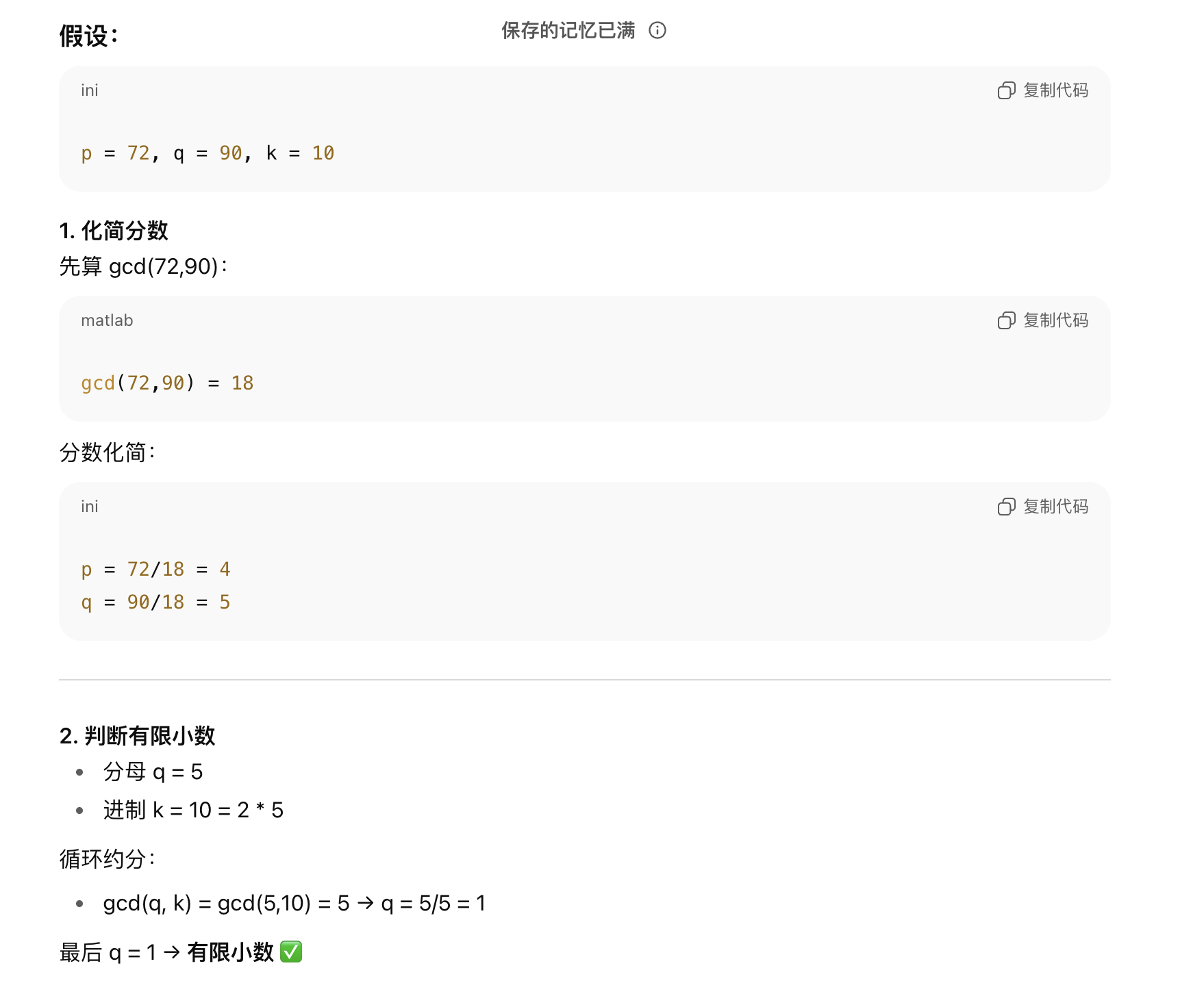
p=1，q=3，k=10
//求p和q的最大公约数
long res=gcd(p,q)；//res=gcd=1；
q=q/res；//q=3/1=3；
g=gcd（q，k）=1，break

import java.util.Scanner;public class solution3 {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int t = sc.nextInt();for (int i = 0; i < t; i++) {long p = sc.nextLong();long q = sc.nextLong();long k = sc.nextLong();System.out.println(Pri(p, q, k));}sc.close();}// 判断是否是有限小数public static String Pri(long p,long q,long k){//把分数化成最简分数，去掉 p 和 q 的最大公因子。这样剩下的 q 才是真正要判断的分母。long res=gcd(p,q);q=q/res;while(true){ long g = gcd(q, k);if (g == 1) break;q /= g;  // 继续用 k 的质因子约掉 q}//return (q==1)?"yes":"no";if(q==1){return "yes";}else{return "no";}}public static long gcd(long p,long q){while(q!=0){long tmp=p%q;p=q;q=tmp;}return p;}}