数据结构青铜到王者第十三话---优先级队列(堆)(2)
续接上一话
目录
一、常见接口的介绍(续)
1、 PriorityQueue常用接口介绍
1.1优先级队列的构造
1.2插入/删除/获取优先级最高的元素
1.3oj练习
二、堆的应用
1、PriorityQueue的实现
2、堆排序
3、Top-k问题
一、常见接口的介绍(续)
1、 PriorityQueue常用接口介绍
1.1优先级队列的构造
此处只是列出了PriorityQueue中常见的几种构造方式

static void TestPriorityQueue(){// 创建一个空的优先级队列,底层默认容量是11PriorityQueue<Integer> q1 = new PriorityQueue<>();// 创建一个空的优先级队列,底层的容量为initialCapacityPriorityQueue<Integer> q2 = new PriorityQueue<>(100);ArrayList<Integer> list = new ArrayList<>();list.add(4);list.add(3);list.add(2);list.add(1);// 用ArrayList对象来构造一个优先级队列的对象// q3中已经包含了三个元素PriorityQueue<Integer> q3 = new PriorityQueue<>(list);System.out.println(q3.size());System.out.println(q3.peek());}#注:默认情况下,PriorityQueue队列是小堆,如果需要大堆需要用户提供比较器
// 用户自己定义的比较器:直接实现Comparator接口,然后重写该接口中的compare方法即可
class IntCmp implements Comparator<Integer>{@Overridepublic int compare(Integer o1, Integer o2) {return o2-o1;}}public class TestPriorityQueue {public static void main(String[] args) {PriorityQueue<Integer> p = new PriorityQueue<>(new IntCmp());p.offer(4);p.offer(3);p.offer(2);p.offer(1);p.offer(5);System.out.println(p.peek());}}此时创建出来的就是一个大堆。
1.2插入/删除/获取优先级最高的元素
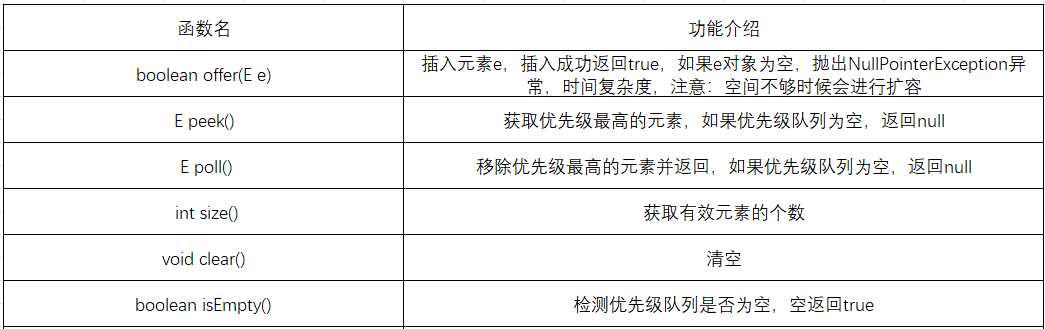
System.out.println(p.peek());}}static void TestPriorityQueue2(){int[] arr = {4,1,9,2,8,0,7,3,6,5};// 一般在创建优先级队列对象时,如果知道元素个数,建议就直接将底层容量给好// 否则在插入时需要不多的扩容// 扩容机制:开辟更大的空间,拷贝元素,这样效率会比较低PriorityQueue<Integer> q = new PriorityQueue<>(arr.length);for (int e: arr) {q.offer(e);}System.out.println(q.size()); // 打印优先级队列中有效元素个数System.out.println(q.peek()); // 获取优先级最高的元素// 从优先级队列中删除两个元素之和,再次获取优先级最高的元素q.poll();q.poll();System.out.println(q.size()); // 打印优先级队列中有效元素个数System.out.println(q.peek()); // 获取优先级最高的元素q.offer(0);System.out.println(q.peek()); // 获取优先级最高的元素// 将优先级队列中的有效元素删除掉,检测其是否为空q.clear();if(q.isEmpty()){System.out.println("优先级队列已经为空!!!");}else{System.out.println("优先级队列不为空");}}#注:以下是JDK 1.8中,PriorityQueue的扩容方式:
private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8;private void grow(int minCapacity) {int oldCapacity = queue.length;// Double size if small; else grow by 50%int newCapacity = oldCapacity + ((oldCapacity < 64) ?(oldCapacity + 2) :(oldCapacity >> 1));// overflow-conscious codeif (newCapacity - MAX_ARRAY_SIZE > 0)newCapacity = hugeCapacity(minCapacity);queue = Arrays.copyOf(queue, newCapacity);}private static int hugeCapacity(int minCapacity) {if (minCapacity < 0) // overflowthrow new OutOfMemoryError();return (minCapacity > MAX_ARRAY_SIZE) ?Integer.MAX_VALUE :MAX_ARRAY_SIZE;}优先级队列的扩容说明:
(1)如果容量小于64时,是按照oldCapacity的2倍方式扩容的
(2)如果容量大于等于64,是按照oldCapacity的1.5倍方式扩容的
(3)如果容量超过MAX_ARRAY_SIZE,按照MAX_ARRAY_SIZE来进行扩容
1.3oj练习
top-k问题:最大或者最小的前k个数据。比如:世界前500强公司
(面试题 17.14. 最小K个数 - 力扣(LeetCode))
我们用一个大根堆实时维护数组的前 k 小值。
首先将前 k 个数插入大根堆中,随后从第 k+1 个数开始遍历,如果当前遍历到的数比大根堆的堆顶的数要小,就把堆顶的数弹出,再插入当前遍历到的数。最后将大根堆里的数存入数组返回即可。
class Solution {public int[] smallestK(int[] arr, int k) {int[] vec = new int[k];// 参数检测if (arr == null||k <= 0) { return vec;}PriorityQueue<Integer> queue = new PriorityQueue<Integer>(new Comparator<Integer>() {public int compare(Integer num1, Integer num2) {return num2 - num1;}});//将数组中的元素依次放到堆中for (int i = 0; i < k; ++i) {queue.offer(arr[i]);}for (int i = k; i < arr.length; ++i) {if (queue.peek() > arr[i]) {queue.poll();queue.offer(arr[i]);}}// 将优先级队列的前k个元素放到数组中for (int i = 0; i < k; ++i) {vec[i] = queue.poll();}return vec;}
}该解法只是PriorityQueue的简单使用,并不是topK最好的做法,那topk该如何实现?下面介绍:
二、堆的应用
1、PriorityQueue的实现
用堆作为底层结构封装优先级队列
2、堆排序
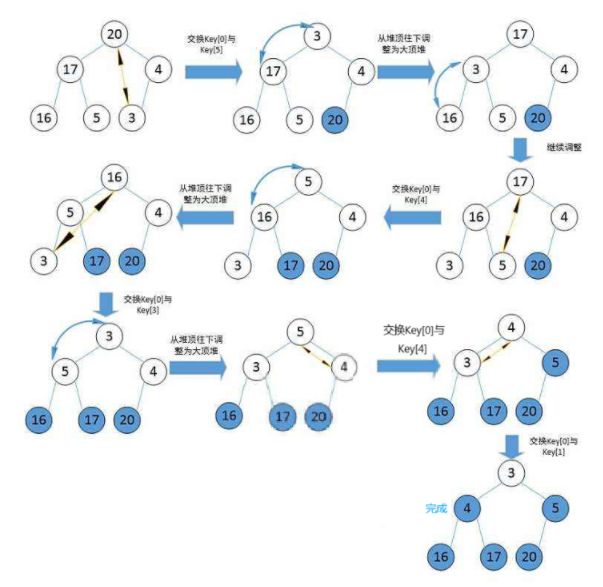
堆排序即利用堆的思想来进行排序,总共分为两个步骤:
(1)建堆:
升序:建大堆
降序:建小堆
(2)利用堆删除思想来进行排序
建堆和堆删除中都用到了向下调整,因此掌握了向下调整,就可以完成堆排序。
3、Top-k问题
TOP-K问题:即求数据集合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大。
比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题,能想到的最简单直接的方式就是排序,但是:如果数据量非常大,排序就不太可取了(可能数据都 不能一下子全部加载到内存中)。最佳的方式就是用堆来解决,基本思路如下:
(1)用数据集合中前K个元素来建堆
前k个最大的元素,则建小堆
前k个最小的元素,则建大堆
(2)用剩余的N-K个元素依次与堆顶元素来比较,不满足则替换堆顶元素
将剩余N-K个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
【具体代码实现,见下一话!!!】
