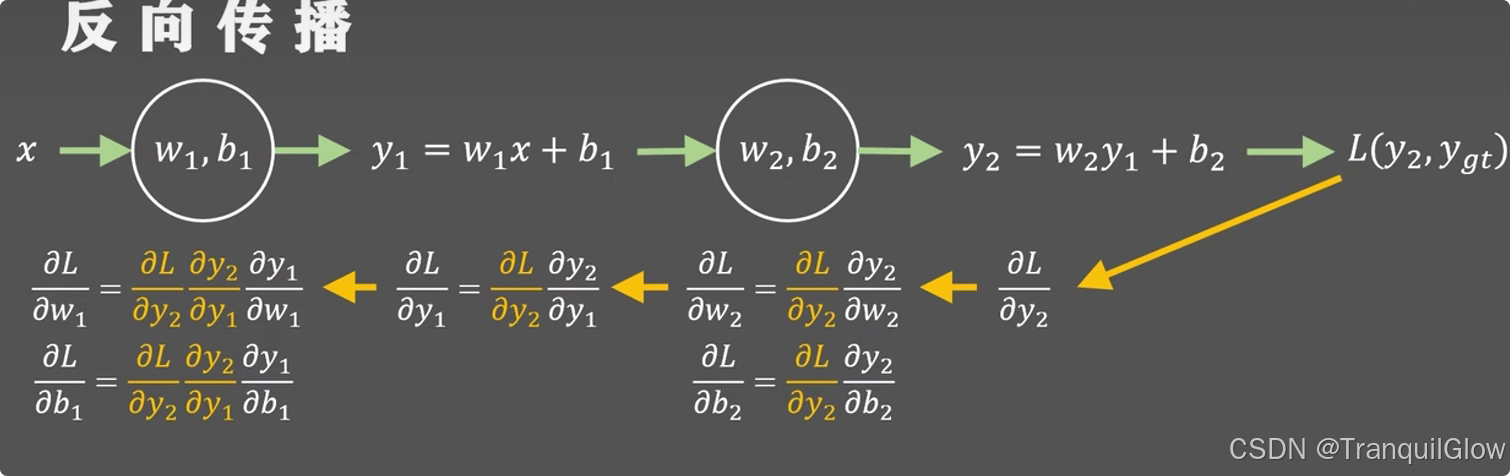深度学习入门，基于python的理论与实现

感知机

介绍

感知机接收多个输入信号，输出一个信号。
每个输入信号都有要给权重，权重越大，信号的重要性就越高

具体的实例可以参考这个与非门
输入0，0输出0，输入0，1输出0，输入1，0输出0，输入1，1输出1
这个感知机就实现了类似于与非门的功能，将多个信号联系上权重，进行输出

具体公式如下：

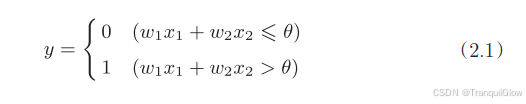
利用Numpy来实现感知机

import numpy as npdef AND(x1,x2):x = np.array([x1, x2])w = np.array([0.5, 0.5])b = -0.7tmp= np.sum(w*x)+bif tmp>0:return 1else:return 0print(AND(0,0),AND(1,1),AND(0,1),AND(1,0))

权重是控制输入信号重要性的参数，偏执是调整神经元被激活的容易程度

感知机局限性

感知器可以实现与门，与非门，或门三种逻辑电路，但是对于异或门来说去而无法实现。
​
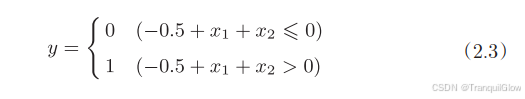
参考这个感知机函数可以得知，这个感知机本质上是由直线-0.5+x1+x2=0分割开的两个空间，其中一个空间输出1，另一个空间输出0

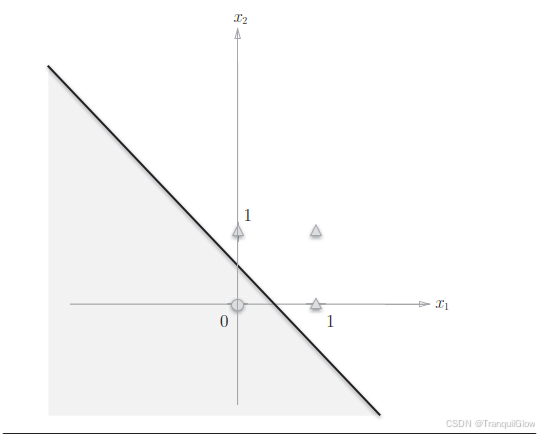
而不可能存在一条直线，使得

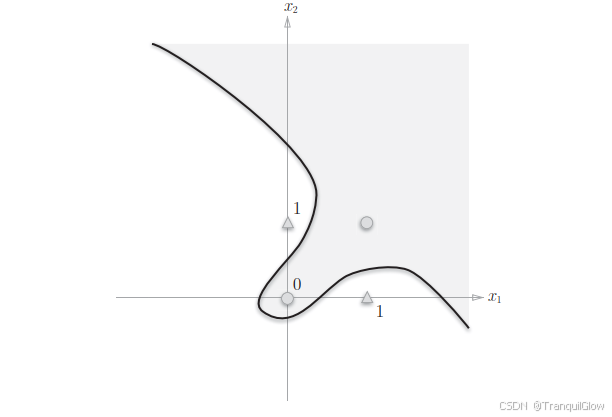
故我们可以使用这个多层感知机，利用或门和与门等的拼接来实现这个异或门的效果。

以此类推，无论多复杂的函数，感知机都隐含着能够表示它的可能性。

神经网络

神经网络介绍

感知机能够表示计算机中进行的各种复杂处理，但是对于设定权重，确定合适能符合与其的输入与输出的权重，现在还是由人工进行的。

神经网络的出现可以解决感知机的缺陷，神经网络相比感知机的优势在沿途，它可以自动地从数据中学习到合适的权重参数。

用图来表示神经网络的结构
最左边的一列称为输入层，最右边的一列称为输出层，中间的一列称为中间层（隐藏层）

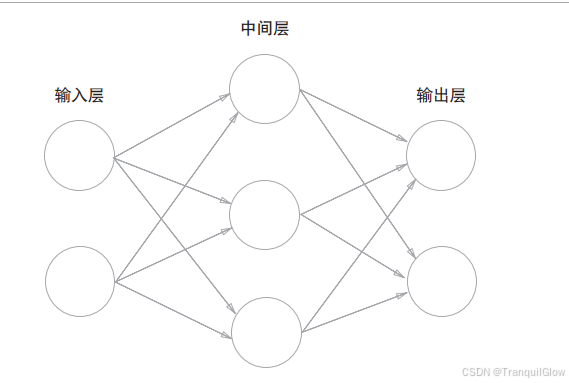
激活函数——连接感知机和神经网络的桥梁

介绍

激活函数将输入信号的综合转换为输出信号
激活函数的作用在于决定如何激活输入信号的总和

‍

$$\begin{gathered} a=b+w_1{x}_1+w_2{x}_2(3.4) \\ y=h(a)(3.5) \end{gathered}$$

3.4 就算加权输入信号和偏置的总和，记为a，然后式（3.5）用h()函数将a转换为输出y

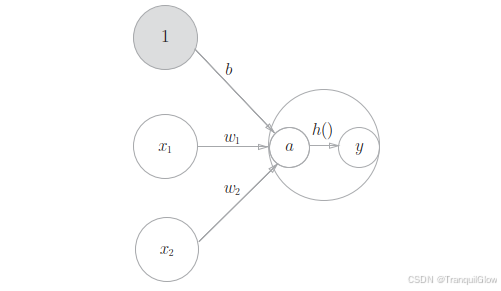
激活函数以阈值为界，一旦输入超过阈值，就切换输出
这样的函数称为“阶跃函数”比如x>0的时候输出1，x<0的时候输出0
感知机使用的就是阶跃函数，我们也利用感知机的这种性质实现了与门，非门等
如果将激活函数从饥饿月函数换成其它函数，就可以进入神经网络的世界了

阶跃函数-感知机函数

阶跃函数的代码实现

如果单纯只是对一个数操作
def step_function(x):if x>0:return 1else:return 0但是很多时候我们并不是单纯只是对一个数进行操作，我们还会对一个数组进行操作，我们引入numpy，已知numpy数组利用比较符是可以直接对其内部所有元素进行操作的
import numpy as np
x = np.array([-1.0,1.0,2.0])
y = x>0
y  # array([False,  True,  True])故这个阶跃函数可以转换为下面的式子，这个astype是将布尔转化为int类型
def step_function(x):y =x>0return y.astype(np.int)

阶跃函数的图形表示

import matplotlib.pylab as plt
x = np.arange(-5.0,5.0,0.1)
y = step_function(x)plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show

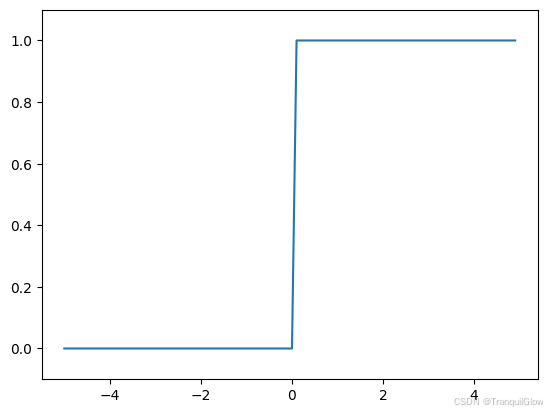
阶跃函数以0为界，输出从0切换到1，它的值呈阶梯式变化，所以称为阶跃函数

sigmoid函数-神经网络函数

$$h(x)=\frac{1}{1+\exp (-x)}\text{\hspace{1em}(3.6)}$$

e是纳皮尔常数2.7182 . . . 。函数给定某个输入后，会返回某个输出
向sigmoid函数输入1.0或2.0后，就会有某个值被输出，类似h(1.0) = 0.731. . .h(2.0) = 0.880 . . .
神经网络中用sigmoid函数作为激活函数，进行信号的转换，转换后的信号被传送给下一个神经元。

阶跃函数的实现:

def sigmoid(x):return 1/(1+np.exp(-x))
x = np.arange(-5.0,5.0,0.1)
y = sigmoid(x)plt.plot(x,y)
plt.ylim(-0.1,1.1)
plt.show

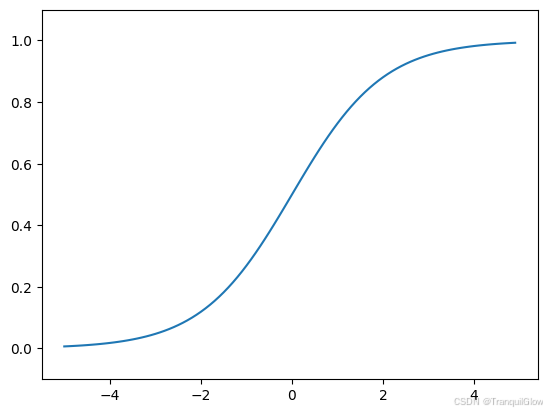
总结

阶跃函数和sigmoid函数一个是感知机函数，一个是神经网络函数

相比感知机信号只能返回0和1，sigmoid函数是连续性的实数值信号

非线性函数

阶跃函数和sigmoid函数都是非线性函数

神经网络的激活函数必须使用非线性函数，如果使用线性函数，那么加深网络的层数就没有意义了。
比如h(x)=cx，那么y(x) = h(h(h(x)))看上去对应的是三层神经网络，但是这个y(x) =$c\ast c\ast c\ast x$的乘法运算，无法发挥出多层网络的作用

ReLU函数

最近最常使用的函数时ReLU函数

ReLU函数在输入大于0的时候，直接输出该值，在输入小于0的时候，输出0

$$h(x)=\{\begin{array}{ll}x& (x>0)\\ 0& (x\le 0)\end{array}$$

def relu(x):return np.maximum(x,0)

多维数组的计算

我们可以使用numpy库来生成多维数组，具体实现方式为np.array([[],[]])
需要注意的是这个array中以中括号为界，里面可以直接放数字代表n*1​ ，如果放的是n个m个元素的数组那么代表的是​n*m​

如果想要知道数组的维数可以使用np.ndim(数组)
如果想要知道数组几行几列可以使用np.shape(数组)​

矩阵的乘法就是行列式的乘法，通过左边矩阵的行（横向）和右边矩阵的列（纵向）以对应元素的方式相乘后在求和而得到的。并且，运算的结果保存为新的多维数组的元素。可以使用np.dot(A,B)来实现。如果矩阵无法进行相乘的话，会报错（左边矩阵的列数必须和右边矩阵的行数相同）

X = np.array([1.0,0.5])
W1 = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])
B1 = np.array([0.1,0.2,0.3])
print(X.shape)
print(W1.shape)
print(B1.shape)ANS = np.dot(W1,B1)
ANS

各层间信号传递的实现

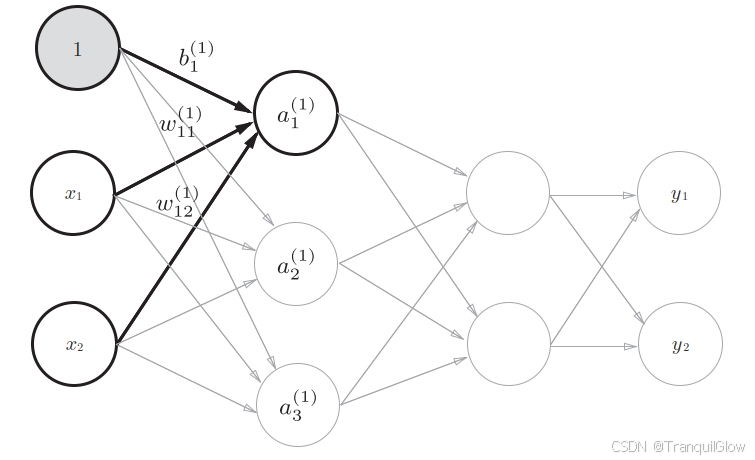
符号解释：

• $a_1^{\left(1\right)}$下标1代表序号，表示该层的第几个神经元吧，上标(1)表示第几层
• $w_{12}^{\left(1\right)}$表示

了解了这些符号之后，这个神经网络的信号传递就可以用

不过有一点需要注意的是，这个输出的信号还需要使用激活函数进行激活，这一点在代码编写的时候会体现出来

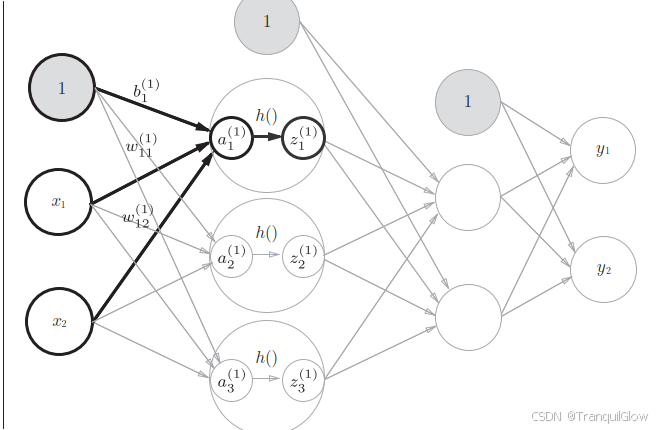
代码实现

def init_network():network = {}network['W1'] = np.array([[0.1,0.3,0.5],[0.2,0.4,0.6]])network['b1'] = np.array([0.1,0.2,0.3])network['W2'] = np.array([[0.1,0.4],[0.2,0.5],[0.3,0.6]])network['b2'] = np.array([0.1,0.2])network['W3'] = np.array([[0.1,0.3],[0.2,0.4]])network['b3'] = np.array([0.1,0.2])return networkdef forward(network,x):W1,W2,W3 = network['W1'],network['W2'],network['W3']b1,b2,b3 = network['b1'],network['b2'],network['b3']a1 = np.dot(x,W1)+b1z1 = sigmoid(a1)a2 = np.dot(z1,W2)+b2z2 = sigmoid(a2)a3 = np.dot(z2,W3)+b3y = a3return ynetwork = init_network()
x = np.array([1.0,0.5])
y = forward(network,x)
y

输出层的设计

针对不同的任务，我们选取不同的激活函数
回归问题用恒等函数，分类问题用softmax函数
分类问题是数据属于哪一类别的问题，回归问题是根据输入预测一个数值的问题。

恒等函数是将输入按原样输出，对于输入的信息，不加以任何改动地直接输出
在输出层使用恒等函数时输入信号会原封不动地被输出。

softmax函数

分类问题使用的softmax函数可以用下式来表示

$$y_k=\frac{\exp (a_k)}{{\sum }_{i=1}^n\exp (a_i)}$$

从这个函数可以看出输出受到前一层每一个输入信号的影响。

代码实现如下：

def softmax(a):exp_a = np.exp(a)sum_exp_a = np.sum(exp_a)y= exp_a/sum_exp_areturn y

需要注意的是exp在进行计算的时候很容易溢出，所以softmax函数可以改进如下：

$$\begin{array}{rl}{y}_k& =\frac{\exp (a_k)}{{\sum }_{i=1}^n\exp (a_i)}=\frac{C\exp (a_k)}{C{\sum }_{i=1}^n\exp (a_i)}\\ & =\frac{\exp (a_k+\log C)}{{\sum }_{i=1}^n\exp (a_i+\log C)}\\ & =\frac{\exp (a_k+C^{\prime })}{{\sum }_{i=1}^n\exp (a_i+C^{\prime })}\end{array}$$

先在分子和分母上都乘上C这个任意的常数。然后，把这个C移动到指数函数（exp）中，记为 log C。最后，把 log C替换为另一个符号C`
在进行softmax的指数函数的运算时，加上（或者减去）某个常数并不会改变运算的结果。这里的C`可以使用任何值，但是为了防止溢出，一般会使用输入信号中的最大值。我们来看一个具体的例子

a = np.array([1010, 1000, 990])
np.exp(a) / np.sum(np.exp(a)) # 无法计算
c = np.max(a) # 1010
a - c
np.exp(a - c) / np.sum(np.exp(a - c))

通过减去输入信号中的最大值（上例中的c），我们发现原本为nan（not a number，不确定）的地方，现在被正确计算

softmax函数的输出是 0.0到 1.0之间的实数。并且，softmax函数的输出值的总和是 1。输出总和为 1是softmax函数的一个重要性质
可以把softmax函数的输出解释为“概率”

正是这个概率特征，所以我们可以用softmax进行分类，看是什么样的概率最高。

输出层的神经元数量需要根据待解决的问题来决定。对于分类问题，输出层的神经元数量一般设定为类别的数量。比如，对于某个输入图像，预测是图中的数字0到9中的哪一个的问题（10类别分类问题)，可以将输出层的神经元设定为10个。

Minist手写数字识别

从网上下载这个数据

# coding: utf-8
import urllib.request
import os.path # 文件夹
import gzip # 解压工具
import pickle # 把处理好的Numpy数组序列化为mnist.pkl。下次直接读磁盘缓存
import os 
import numpy as np #：所有矩阵、向量都用 np.ndarray 表示#下载的文件
url_base = 'https://ossci-datasets.s3.amazonaws.com/mnist/'
key_file = {'train_img':'train-images-idx3-ubyte.gz','train_label':'train-labels-idx1-ubyte.gz','test_img':'t10k-images-idx3-ubyte.gz','test_label':'t10k-labels-idx1-ubyte.gz'
}# __file__  只是“当前脚本文件”的路径字符串（可能是相对路径，也可能是绝对路径，取决于你如何启动脚本
# os.path.abspath 返回文件的绝对滤镜
#  os.path.dirname去掉文件名
dataset_dir = os.path.dirname(os.path.abspath(__file__))
save_file = dataset_dir + "/mnist.pkl"train_num = 60000
test_num = 10000
img_dim = (1, 28, 28)
img_size = 784def _download(file_name):file_path = dataset_dir + "/" + file_nameif os.path.exists(file_path):returnprint("Downloading " + file_name + " ... ")urllib.request.urlretrieve(url_base + file_name, file_path)print("Done")def download_mnist():for v in key_file.values():_download(v)def _load_label(file_name):file_path = dataset_dir + "/" + file_nameprint("Converting " + file_name + " to NumPy Array ...")with gzip.open(file_path, 'rb') as f:labels = np.frombuffer(f.read(), np.uint8, offset=8)print("Done")return labelsdef _load_img(file_name):file_path = dataset_dir + "/" + file_nameprint("Converting " + file_name + " to NumPy Array ...")    with gzip.open(file_path, 'rb') as f:data = np.frombuffer(f.read(), np.uint8, offset=16)data = data.reshape(-1, img_size)print("Done")return datadef _convert_numpy():dataset = {}dataset['train_img'] =  _load_img(key_file['train_img'])dataset['train_label'] = _load_label(key_file['train_label'])    dataset['test_img'] = _load_img(key_file['test_img'])dataset['test_label'] = _load_label(key_file['test_label'])return datasetdef init_mnist():download_mnist()dataset = _convert_numpy()print("Creating pickle file ...")with open(save_file, 'wb') as f:pickle.dump(dataset, f, -1)print("Done!")def _change_one_hot_label(X):T = np.zeros((X.size, 10))for idx, row in enumerate(T):row[X[idx]] = 1return Tdef load_mnist(normalize=True, flatten=True, one_hot_label=False):"""读入MNIST数据集Parameters----------normalize : 将图像的像素值正规化为0.0~1.0one_hot_label : one_hot_label为True的情况下，标签作为one-hot数组返回one-hot数组是指[0,0,1,0,0,0,0,0,0,0]这样的数组flatten : 是否将图像展开为一维数组Returns-------(训练图像, 训练标签), (测试图像, 测试标签)"""if not os.path.exists(save_file):init_mnist()with open(save_file, 'rb') as f:dataset = pickle.load(f)if normalize:for key in ('train_img', 'test_img'):dataset[key] = dataset[key].astype(np.float32)dataset[key] /= 255.0if one_hot_label:dataset['train_label'] = _change_one_hot_label(dataset['train_label'])dataset['test_label'] = _change_one_hot_label(dataset['test_label'])if not flatten:for key in ('train_img', 'test_img'):dataset[key] = dataset[key].reshape(-1, 1, 28, 28)return (dataset['train_img'], dataset['train_label']), (dataset['test_img'], dataset['test_label']) if __name__ == '__main__':init_mnist()

神经网络的学习

神经网络的学习是指从训练数据中自动获取最优权重参数的过程，为了使神经网络能够进行学习，将导入损失安徽念书这一指标，学习的目的就是以该损失函数为基准，找出能使它的值达到最小的权重参数。我们就此引入了梯度算法。

机器学习和深度学习

机器学习，机器从收集到的数据中找出规律性，但是需要注意的，将图像转换为向量时使用的特征量仍是由人设计的。对于不同的问题，必须使用合适的特征量。识别人脸和数字就需要认为的设定不同的特征量。

深度学习怎不同，深度学习是利用神经网络直接学习图像本身，图像中的特征量都是机器自己进行学习的。

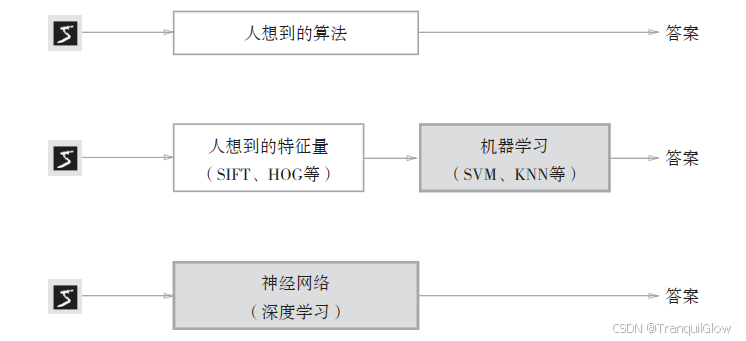
神经网络的优点是对所有的问题都可以用同样的流程来解决

损失函数

常见损失函数由均方差损失函数和交叉熵损失函数

假设我们关注这个神经网络中的某一个权重参数，对该权重参数进行求导，表示的是，如果稍微改变这个权重参数的值，损失函数的值会如何变化。如果导数的值为负，通过是该权重参数想正方向改变，可以减少损失函数的值，反过来也是，当导数的值为0的时候，无论权重参数向哪个方向变化，损失函数的值都不会发生改变。此时该权重参数的更新会停在此处。

在进行神经网络的学习时，不能将识别精度作为指标，因为如果以识别精度为指标，则参数的导数在绝大多数的地方都会变成0（因为你的修改不一定会导致识别精度发生改变）

梯度下降算法

介绍：

• 一个直线$(y=wx+b)$拟合的好不好，我们可以用点到直线的距离来表示
• 当损失函数最小的时候，拟合效果最好

由上图可知我们需要找到这个让损失函数最小的b值，可以使用迭代优化的方法。令

随机梯度下降算法

当斜率为0的时候这个b不改变

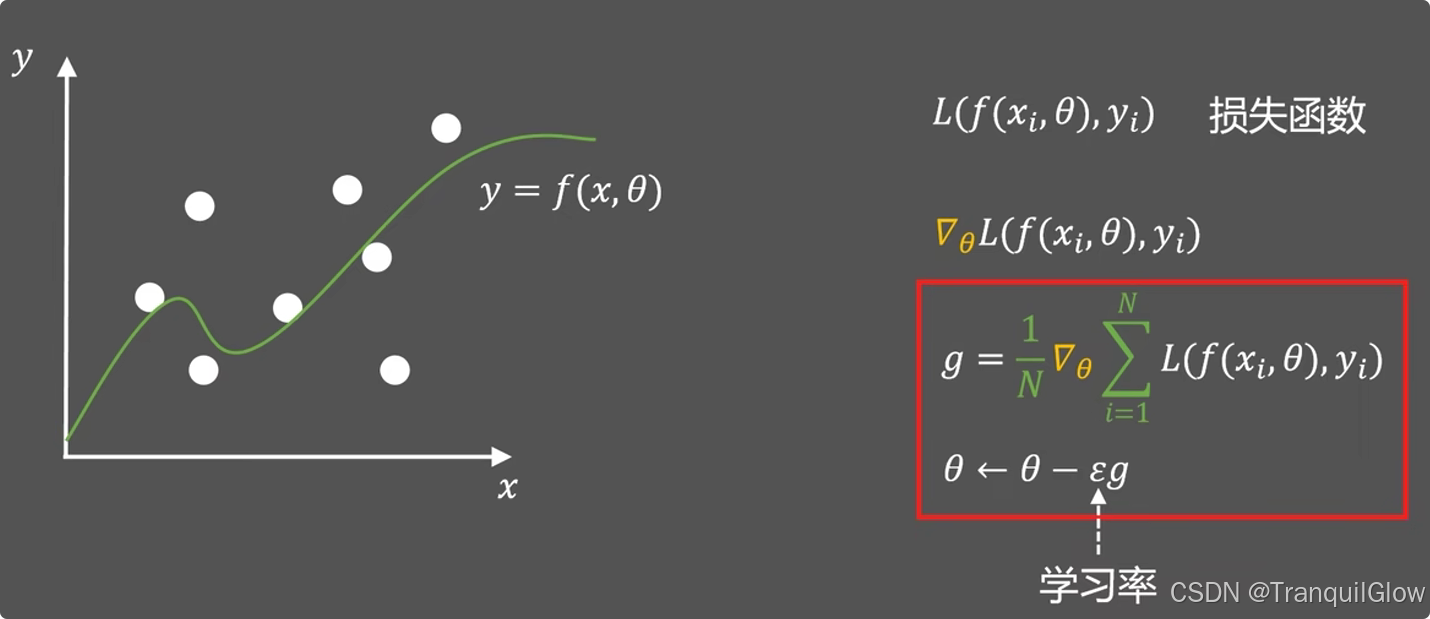
这个$ϵ$是学习率，表示每次改变的步长

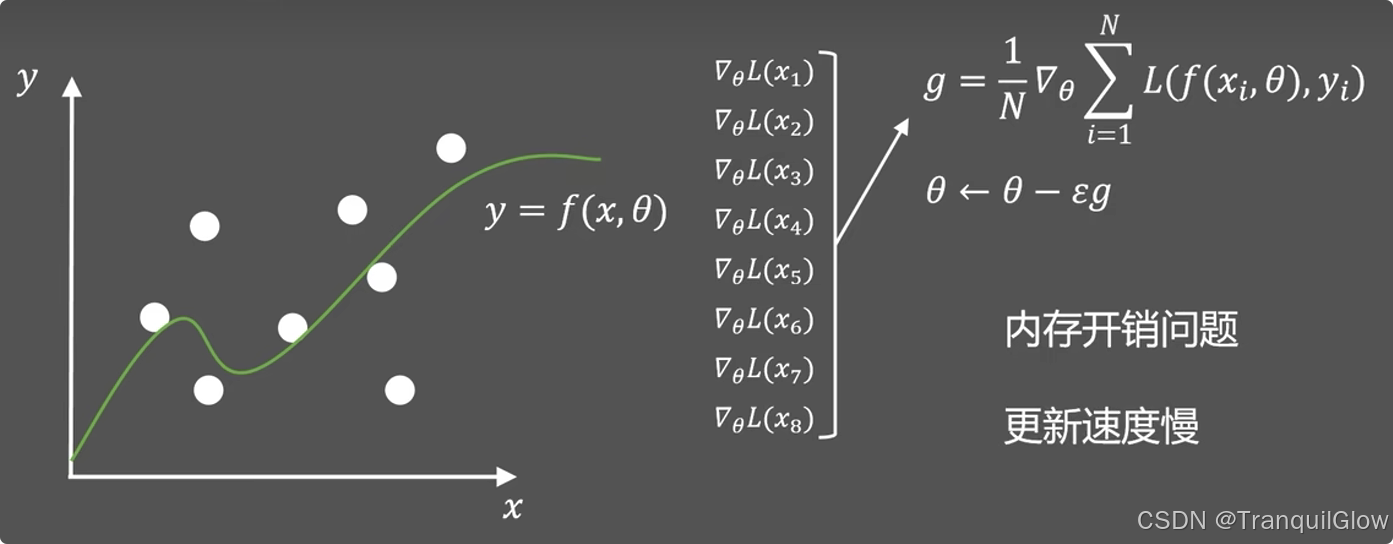
如果每次都需要把这个每个值给保存起来，需要很大的内存开销，同时计算所有的值才更新以此参数，更i性能速度也会变慢。

改进方法：我们每次可以从n个样本中随机选取m个样本进行更新，并且每次都不重复，这种改进方法被称为随机梯度下降算法

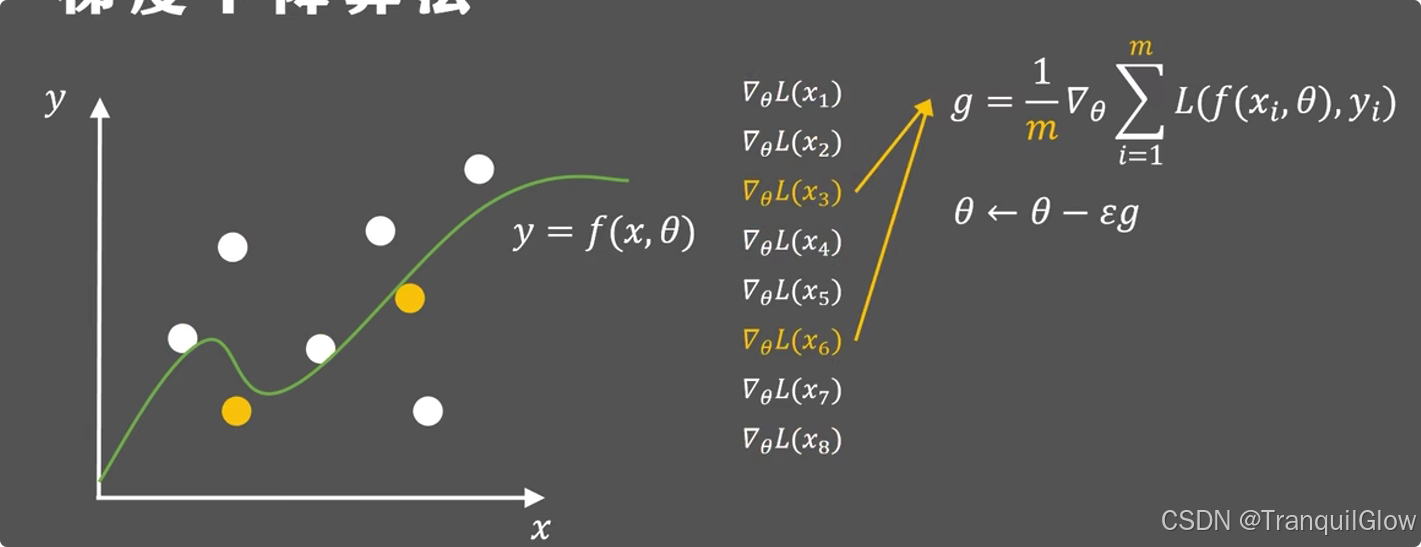
动量随机梯度下降

这个方法关键就在于
参数的移动受到来自梯度的一个力，但是它仍然要保留原始运动状态的一部分速度，所以运动起来速度才会更加平滑。

学习率

最初的时候，学习率刚开始设置一个很大的值，希望能够尽快的找到收敛方向，之后，设置逐渐减少。

现如今，学习率可以根据梯度来进行调整，r是梯度的积累量，当这个r变化很快的时候，这个学习率就会快速下降，当这个r变换很慢的时候，这个学习率就会下降慢一些。其中$\delta$是一个小量，用来稳定数值计算的。

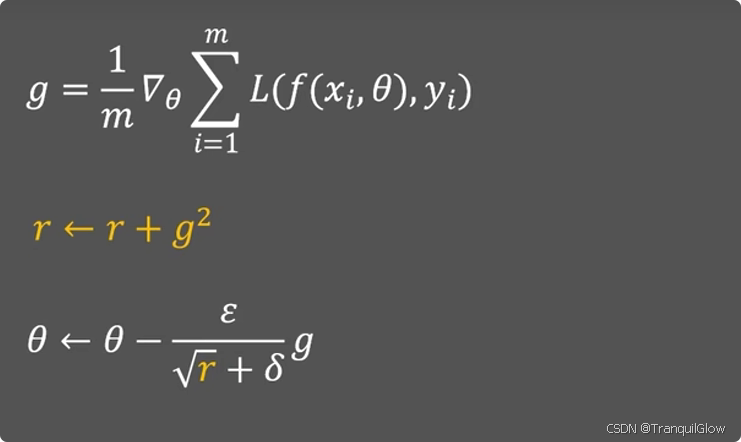
后来发现这个r的变化只与梯度有关，可能让学习率过早的变小而不好控制，所以后来在r更新的公式中，加入可以手动调节的$\rho$，用来控制优化过程。

Adam算法

兼顾动量和自动调节

‍

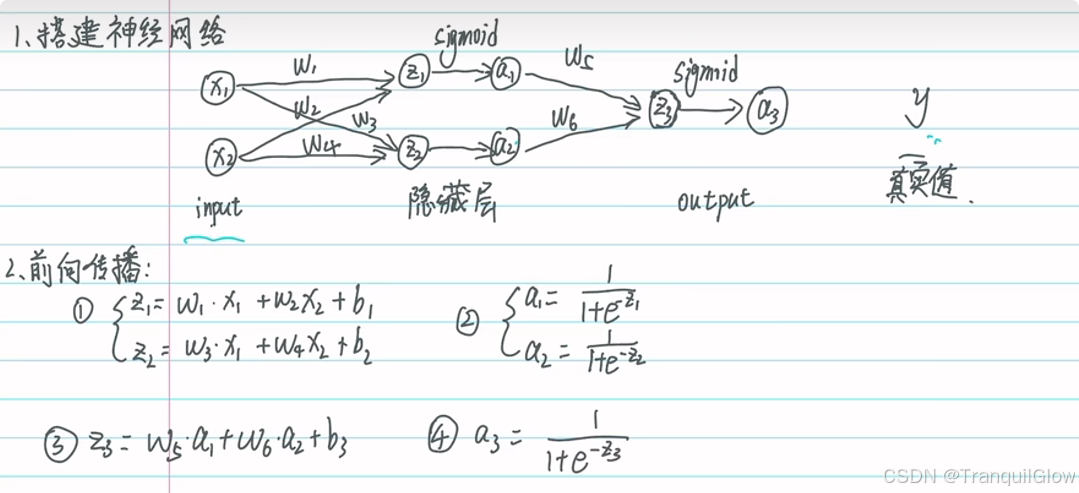
前向传播和反向传播

神经网络的推理过程就是神经网络的前向传播，就是神经网络的正向推理流程。

从后向前计算参数梯度值的算法就是反向传播算法。

先把误差从输出层一路量回到每一层，再用链式法则算出每个参数该负多大责任，最后按责任大小更新权重。

1. 场景：前向之后有了误差

   1. 输入 x → 神经网络 → 输出 ŷ
   2. 与真实标签 y 比较，得到损失 L(ŷ, y)
   3. 目标：调所有权重 W，让 L 变小

2. 数学核心：链式法则

   1. 对任意权重 $w_{ij}$，想知道$\delta L/\delta w_{ij}$(如果把权重​**$w_{ij}$** 微微增大一点点，损失 L 会增加或减少多少)

      1. 数值上：它是损失函数对第 i 个神经元到第 j 个神经元那条连边权重的偏导数。
      2. 几何上：它是误差曲面在 $w_{ij}$方向上的斜率（梯度在这一维的分量
      3. 乘以学习率 η 就直接得到“该权重在这次迭代中应该修正的步长.

   2. 计算过程

      1. 先求$\delta L/\delta ŷ $（损失对输出）
      2. 再乘以$\delta \hat{y}/\delta z$（激活函数）
      3. 再乘 $\delta z/\delta w_{ij}$（线性组合）

原理讲解：

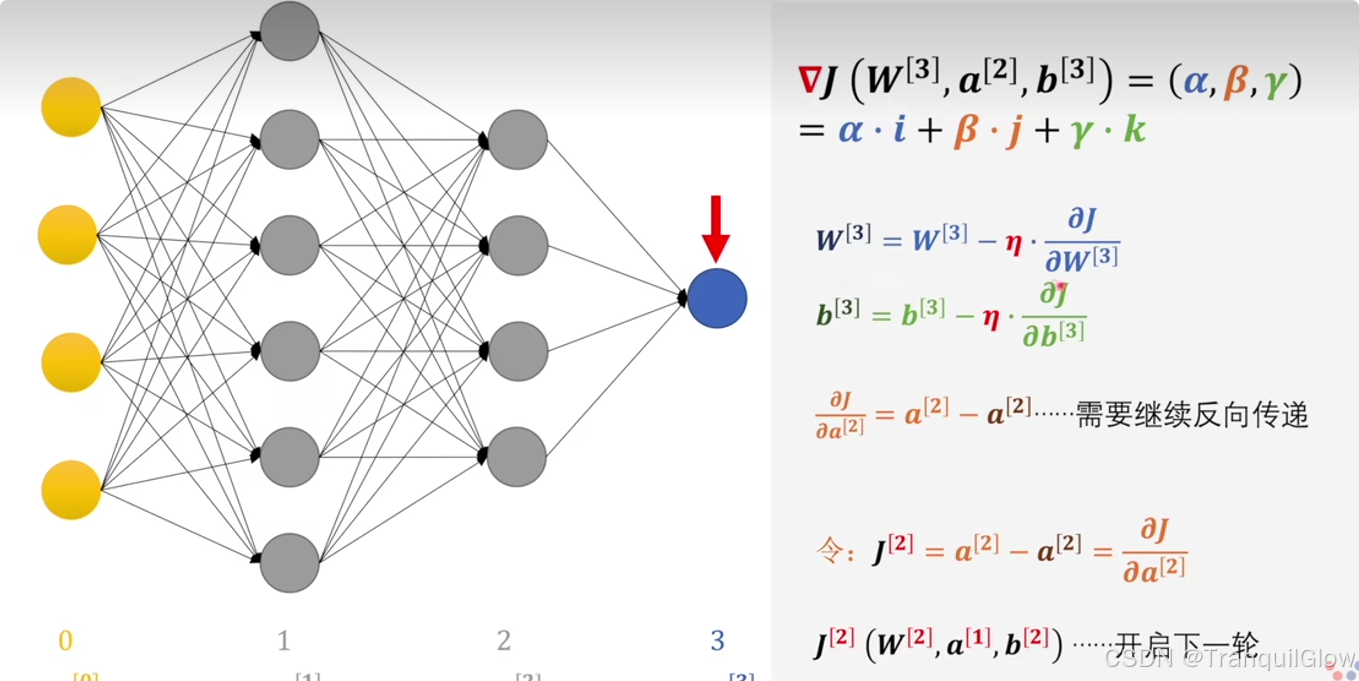
公式中的两个 a[2] 并非完全相同：第一个 a[2] 是前向传播时计算得到的实际激活值，而第二个 a[2] 则是从后一层（第三层）反向传播回来的、与当前层相关的梯度信息。它们的差值 J[2] 实际上代表了当前层对总损失的贡献，或者说误差在当前层的表示。

1. 反向传播 = 链式法则 + 缓存 + 局部更新​

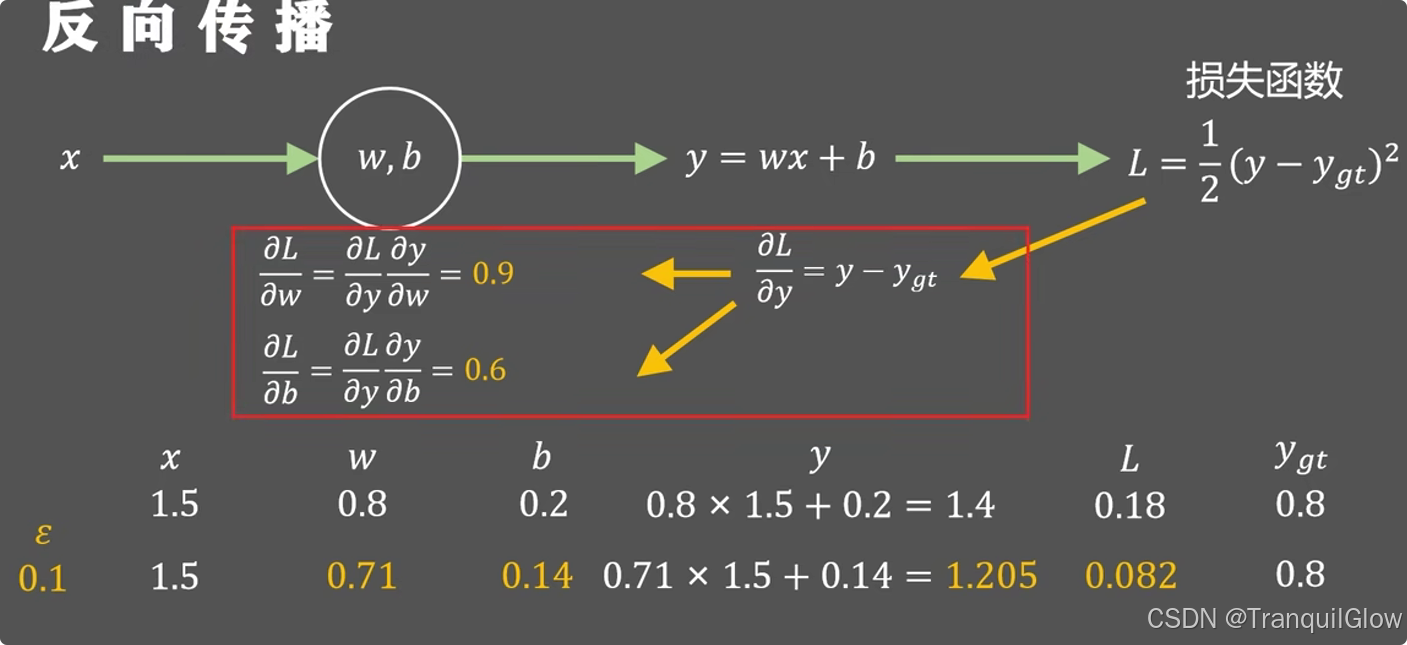
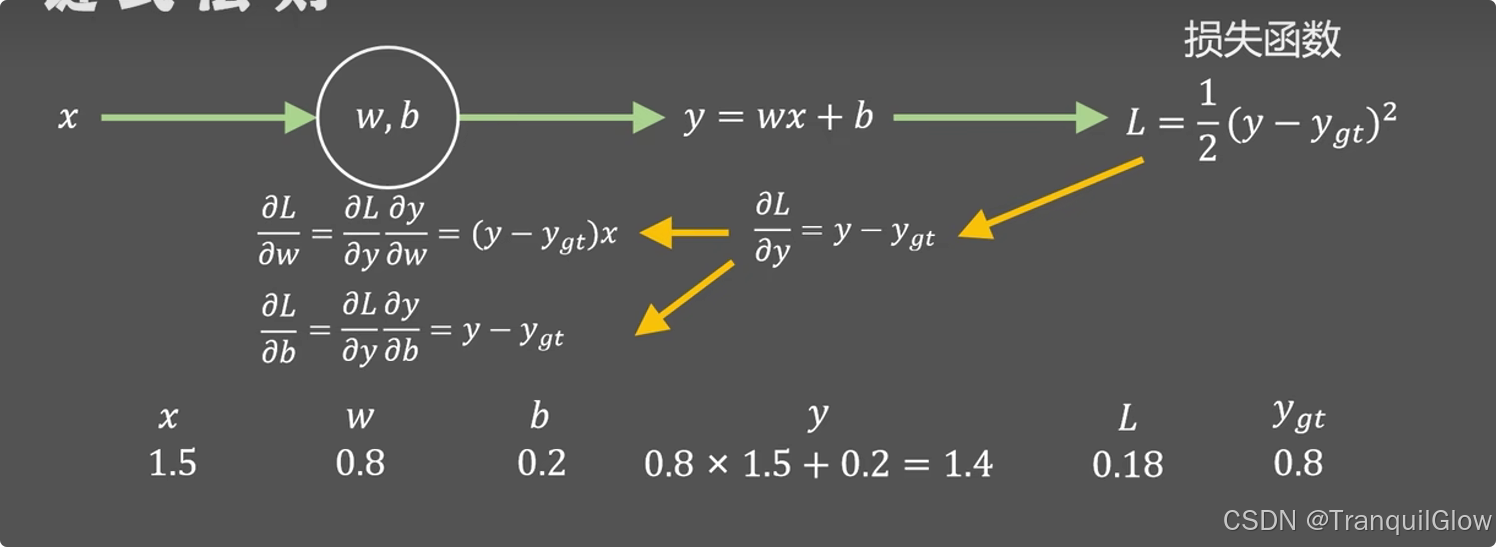
同时反向传播还有一个好处就是能够加快运算过程，后一步的计算结果可以用到下一步中，避免了重复计算