FPGA增量式方差与均值计算
设有一离散序列xi(i=1,2...,n),其数学均值μ与方差σ2传统计算方式如下:
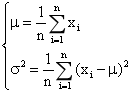
该方法的缺陷在于,每次新增一个数据点时,都需要重新遍历全部历史数据以更新均值与方差,这在实际的实时信号处理系统中难以实现,尤其当数据量较大时,计算效率将显著下降。为解决这一问题,本设计采用Welford递推算法,实现对均值与方差的增量式更新,从而避免对历史数据的重复访问与遍历,显著提升计算效率。
Welford 算法的递推公式如下:
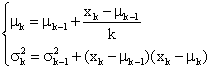
其中
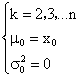
module exp_var_calc(input i_clk ,input i_rst ,input [31:0] i_data ,input i_start ,output reg [31:0] o_exp ,output reg [79:0] o_var ,output reg o_done ,output o_ready);(*max_fanout = 20, keep = "true"*)reg [12:0] r_cstate ;reg [12:0] r_nstate ;localparam S_IDLE = 13'b0000000000001 , S_STEP0 = 13'b0000000000010 ,//delta0S_STEP1 = 13'b0000000000100 ,//delta0 / iS_STEP2 = 13'b0000000001000 ,S_STEP3 = 13'b0000000010000 ,//exp + delta0 / iS_EXP = 13'b0000000100000 ,S_STEP4 = 13'b0000001000000 ,//delta1S_STEP5 = 13'b0000010000000 ,//delta0 * delta1S_STEP6 = 13'b0000100000000 ,//平方偏差累积S_STEP7 = 13'b0001000000000 ,S_STEP8 = 13'b0010000000000 ,//平方偏差累积 / (i - 1)S_VAR = 13'b0100000000000 ,S_DONE = 13'b1000000000000 ;// 寄存输入值reg signed [47:0] r_data_reg ;wire signed [47:0] w_data_reg ;assign o_ready = r_cstate == S_IDLE;always@(posedge i_clk or posedge i_rst) beginif(i_rst)r_data_reg <= 'd0;else if(i_start & r_cstate == S_IDLE)r_data_reg <= w_data_reg;else r_data_reg <= r_data_reg;endwire [47:0] w_exp;bit_extension# (.BW_IN (32'd32 ),.BW_OUT (32'd48 ),.SIGNED (1'b1 ))
data_ext_u(.i_data (i_data ),.o_data (w_data_reg )
);bit_extension# (.BW_IN (32'd32 ),.BW_OUT (32'd48 ),.SIGNED (1'b1 ))
exp_ext_u(.i_data (o_exp ),.o_data (w_exp )
);// STEP0 startwire signed [47:0] w_delta0 ;addsub_S48S48
delta0 (.A (r_data_reg ), // input wire [47 : 0] A.B (w_exp ), // input wire [47 : 0] B.CLK(i_clk ), // input wire CLK.ADD(1'b0 ), // input wire ADD.CE (1'b1 ), // input wire CE.S (w_delta0 ) // output wire [47 : 0] S
);// STEP0 end// STEP1 start(*max_fanout = 20, keep = "true"*)reg [15:0] r_din_cnt ;always@(posedge i_clk or posedge i_rst) beginif(i_rst)r_din_cnt <= 'd0;else if(r_cstate == S_IDLE & i_start) r_din_cnt <= r_din_cnt + 1'd1;else r_din_cnt <= r_din_cnt;endreg [15:0] r_divisor_data ;reg [47:0] r_dividend_data ;reg r_dividend_vld ;reg r_divisor_vld ;wire w_dividend_rdy ;wire w_divisor_rdy ;wire w_div_res_vld ;wire [63:0] w_div_res ;wire [47:0] w_quotient ;wire [15:0] w_reminder ;assign w_quotient = w_div_res[63:16];assign w_reminder = w_div_res[15:0];reg signed [47:0] r_round_quotient;always@(posedge i_clk or posedge i_rst) beginif(i_rst)r_round_quotient <= 'd0;else if(w_quotient[47])if(w_reminder >= 16'h8000)r_round_quotient <= $signed(w_quotient) + 'd1;elser_round_quotient <= w_quotient;else if(w_reminder >= 16'h8000)r_round_quotient <= w_quotient + 'd1;else r_round_quotient <= w_quotient;endalways@(posedge i_clk or posedge i_rst) beginif(i_rst) beginr_dividend_data <= 'd0;r_divisor_data <= 'd0;r_dividend_vld <= 'd0;r_divisor_vld <= 'd0;endelse if(r_cstate == S_STEP1 & w_dividend_rdy & w_divisor_rdy) beginr_dividend_data <= w_delta0;r_divisor_data <= r_din_cnt;r_dividend_vld <= 'd1;r_divisor_vld <= 'd1;endelse beginr_dividend_data <= r_dividend_data;r_divisor_data <= r_divisor_data;r_dividend_vld <= 'd0;r_divisor_vld <= 'd0;endenddiv_S48S16
delta_div_i (.aclk (i_clk ), // input wire aclk.s_axis_divisor_tvalid (r_divisor_vld ), // input wire s_axis_divisor_tvalid.s_axis_divisor_tready (w_divisor_rdy ), // output wire s_axis_divisor_tready.s_axis_divisor_tdata (r_divisor_data ), // input wire [15 : 0] s_axis_divisor_tdata.s_axis_dividend_tvalid (r_dividend_vld ), // input wire s_axis_dividend_tvalid.s_axis_dividend_tready (w_dividend_rdy ), // output wire s_axis_dividend_tready.s_axis_dividend_tdata (r_dividend_data), // input wire [47 : 0] s_axis_dividend_tdata.m_axis_dout_tvalid (w_div_res_vld ), // output wire m_axis_dout_tvalid.m_axis_dout_tdata (w_div_res ) // output wire [63 : 0] m_axis_dout_tdata
); // STEP1 end// STEP3 startwire [47:0] w_new_exp ;reg r_beat_delay ;//延迟一拍凑时许always@(posedge i_clk or posedge i_rst) beginif(i_rst)r_beat_delay <= 'd0;else if(r_cstate == S_STEP3)r_beat_delay <= 'd1;else r_beat_delay <= 'd0;endaddsub_S48S48
new_exp (.A (r_round_quotient ), // input wire [47 : 0] A.B (w_exp ), // input wire [47 : 0] B.CLK(i_clk ), // input wire CLK.ADD(1'b1 ), // input wire ADD.CE (1'b1 ), // input wire CE.S (w_new_exp ) // output wire [47 : 0] S
);// STEP3 endreg signed [47:0] r_new_exp ;always@(posedge i_clk or posedge i_rst) beginif(i_rst) r_new_exp <= 'd0;else if(r_cstate == S_EXP)r_new_exp <= w_new_exp;else r_new_exp <= r_new_exp;end// STEP4 startwire [47:0] w_delta1;
addsub_S48S48
delta1 (.A (r_data_reg ), // input wire [47 : 0] A.B (r_new_exp ), // input wire [47 : 0] B.CLK(i_clk ), // input wire CLK.ADD(1'b0 ), // input wire ADD.CE (1'b1 ), // input wire CE.S (w_delta1 ) // output wire [47 : 0] S
); // STEP4 end// STEP5 startreg [3:0] r_mult_cnt ;always@(posedge i_clk or posedge i_rst) beginif(i_rst)r_mult_cnt <= 'd0;else if(r_cstate == S_STEP5)r_mult_cnt <= r_mult_cnt + 1;else r_mult_cnt <= 'd0;endwire signed [63:0] w_delta0Xdelta1;
mult_S32S32
delta0_delta1 (.CLK (i_clk ), // input wire CLK.A ({w_delta0[47],w_delta0[30:0]}), // input wire [31 : 0] A.B ({w_delta1[47],w_delta1[30:0]}), // input wire [31 : 0] B.P (w_delta0Xdelta1) // output wire [63 : 0] P
);// STEP5 end// STEP6 startreg [3:0] r_add_cnt ;//延迟计数always@(posedge i_clk or posedge i_rst) beginif(i_rst)r_add_cnt <= 'd0;else if(r_cstate == S_STEP6)r_add_cnt <= r_add_cnt + 1;else r_add_cnt <= 'd0;endwire [79:0] w_sd_acc ;reg signed [79:0] r_sd_acc ;//平方偏差累积always@(posedge i_clk or posedge i_rst) beginif(i_rst)r_sd_acc <= 'd0 ;else if(r_cstate == S_STEP6 & r_add_cnt >= 7) r_sd_acc <= w_sd_acc;else r_sd_acc <= r_sd_acc;endadd_S80S64
ad_acc (.A (r_sd_acc ), // input wire [79 : 0] A.B (w_delta0Xdelta1 ), // input wire [63 : 0] B.CLK(i_clk ), // input wire CLK.S (w_sd_acc ) // output wire [79 : 0] S
); // STEP6 end// STEP7 startreg r_div_start ;wire [79:0] w_new_var ;wire [79:0] w_round_var ;wire w_div_done ;always@(posedge i_clk or posedge i_rst) beginif(i_rst)r_div_start <= 'd0;else if(r_cstate == S_STEP7)r_div_start <= 'd1;else r_div_start <= 'd0;endwire [15:0] w_var_rem;assign w_round_var = w_var_rem >= (r_din_cnt >> 1) ? w_new_var + 'd1 : w_new_var;reg [79:0] r_round_var ;always@(posedge i_clk or posedge i_rst) beginif(i_rst)r_round_var <= 'd0;else if(r_cstate == S_VAR) r_round_var <= w_round_var;else r_round_var <= r_round_var;endmy_divider#(.DIVIDEND_BW(80) ,.DIVISOR_BW (16))
my_divider_u(.i_clk (i_clk ),.i_rst (i_rst ),.i_dividend (r_sd_acc ),.i_divisor (r_din_cnt - 1 ),.i_start (r_div_start),.o_quotient (w_new_var ),.o_reminder (w_var_rem ),.o_done (w_div_done )
); always@(posedge i_clk or posedge i_rst) beginif(i_rst) begino_exp <= 'd0;o_var <= 'd0;o_done <= 'd0;endelse if(r_cstate == S_DONE) begino_exp <= r_new_exp;o_var <= r_din_cnt > 1 ? r_round_var : 'd0;o_done <= 'd1;endelse begino_exp <= o_exp;o_var <= o_var;o_done <= 'd0;endendalways@(posedge i_clk or posedge i_rst) beginif(i_rst)r_cstate <= S_IDLE;else r_cstate <= r_nstate;endalways@(*) begincase(r_cstate)S_IDLE: r_nstate = i_start ? S_STEP0 : S_IDLE;S_STEP0: r_nstate = S_STEP1;S_STEP1: r_nstate = w_dividend_rdy & w_divisor_rdy ? S_STEP2 : S_STEP1;S_STEP2: r_nstate = w_div_res_vld ? S_STEP3 : S_STEP2;S_STEP3: r_nstate = r_beat_delay ? S_EXP : S_STEP3;S_EXP: r_nstate = S_STEP4;S_STEP4: r_nstate = S_STEP5;S_STEP5: r_nstate = r_mult_cnt >= 6 ? S_STEP6 : S_STEP5;S_STEP6: r_nstate = r_add_cnt >= 7 ? S_STEP7 : S_STEP6;S_STEP7: r_nstate = S_STEP8;S_STEP8: r_nstate = w_div_done ? S_VAR : S_STEP8;S_VAR: r_nstate = S_DONE;S_DONE: r_nstate = S_IDLE;default: r_nstate = S_IDLE;endcaseendendmodule
逻辑级数比较大,目前勉强跑200mhz,可以在状态机中再加一拍处理round var的逻辑运算,tb文件如下
`timescale 1ns / 1psmodule exp_var_tb();reg i_clk ;reg i_rst ;reg [31:0] i_data ;reg i_start ;wire [31:0] o_exp ;wire [79:0] o_var ;wire o_done ;wire o_ready ;initial begini_clk = 1;i_rst = 1;i_data = 0;i_start = 0;#100;i_rst = 0;repeat(1000) begin#10i_data = $random()%8'hff;i_start = 1;#10i_start = 0;@(posedge o_ready);end#1000$stop;endalways#5 i_clk = ~i_clk;exp_var_calc
exp_var_calc_u(i_clk ,i_rst ,i_data ,i_start ,o_exp ,o_var ,o_done ,o_ready
);endmodule
仿真波形白色是满足[0,255]的均匀分布随机数列,橙色表示均值收敛在127,黄色代表方差收敛在5400左右。

