当前位置：首页 > news >正文

考研数据结构Part3——二叉树知识点总结

news 2025/8/30 8:18:52

一、前言

二叉树是一种特殊的树形结构，每个节点最多有两个子节点，分别称为左子树和右子树。其特点是子树有严格的左右之分，顺序不可颠倒。从历年真题来看，二叉树的链式存储实现、遍历算法、属性统计是高频考点，常以选择题（概念辨析）、填空题（代码补全）、编程题（算法实现）形式出现。

二叉树的常见类型包括：

满二叉树：所有非叶子节点均有两个子节点，且所有叶子节点在同一层。
完全二叉树：除最后一层外，其他层节点数达到最大值，且最后一层节点向左对齐。
二叉搜索树（BST）：左子树所有节点的值小于根节点，右子树所有节点的值大于根节点。

二、二叉树

二叉树通常用链式存储或顺序存储（数组）实现。二叉树的链式存储通过节点连接实现，每个节点包含数据域和两个指针域（分别指向左子树和右子树）。

1.定义

typedef struct BiTNode{char data;struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

2.基本操作

（1）初始化二叉树

初始化操作将二叉树根节点的左右子树指针设为NULL，确保树的初始状态为空。

bool InitBiTree(BiTree &T){T->lchild = NULL;T->rchild = NULL;return true;
}

（2）创建二叉树（递归法）

基于先序遍历规则构建二叉树，通过递归方式依次创建根节点、左子树和右子树，#符号用于标识空节点。

void CreateBiTree(BiTree &T){char ch;scanf("%c",&ch);if(ch=='#')T=NULL;else{T=(BiTNode *)malloc(sizeof(BiTNode));T->data=ch;CreateBiTree(T->lchild);CreateBiTree(T->rchild);}	
}

（3）销毁二叉树

采用后序遍历思路，先递归销毁左、右子树，再释放当前节点，确保所有内存被正确回收。

void DestroyBiTree(BiTree &T){if(T){if(T->lchild)DestroyBiTree(T->lchild);if(T->rchild)DestroyBiTree(T->rchild);	free(T);T=NULL;}
}

（4）遍历操作

二叉树的遍历是访问所有节点的过程，常见方式包括先序、中序、后序（递归 / 非递归）和层序遍历。

先序遍历（递归）

递归实现简洁，先访问当前节点，再依次遍历左、右子树。

//访问输出结点
void visit(BiTree T){printf("%c",T->data);}
//先序-递归
void PreOrder(BiTree T){if(T!=NULL){visit(T);PreOrder(T->lchild);PreOrder(T->rchild);}
}

中序遍历（非递归，借助栈）

非递归实现需借助栈，先将所有左节点入栈，再依次弹出并访问，最后遍历右子树。

void InOrder2(BiTree T){SqStack S;InitStack(S);BiTree p=T;while(p!=NULL||!StackEmpty(S)){if(p){Push(S,p);p=p->lchild;}else{Pop(S,p);visit(p);p=p->rchild;}}
}

层序遍历（借助队列）

利用队列实现，依次将每层节点入队，出队时访问节点并将其子女入队，确保按层次顺序遍历。

void LevelOrder(BiTree T){SqQueue Q;InitQueue(Q);BiTree p;EnQueue(Q,T);while(!IsEmpty(Q)){DeQueue(Q,p);visit(p);if(p->lchild!=NULL){EnQueue(Q,p->lchild);}if(p->rchild!=NULL){EnQueue(Q,p->rchild);}}
}

（5）二叉树的属性统计

二叉树的属性统计是分析树结构特征的重要操作，包括节点类型计数、高度和宽度计算等。这些属性不仅反映了树的形态特征，也为算法设计（如平衡树判断、最优路径搜索）提供基础数据。

统计叶子节点（度为0的节点）

int Degree0(BiTree T){if(T==NULL) return 0;else if(T->lchild==NULL&&T->rchild==NULL) return 1;else return Degree0(T->lchild)+Degree0(T->rchild);
}

统计度为1的节点

int Degree1(BiTree T){if(T==NULL) return 0;if((T->rchild==NULL && T->lchild!=NULL) || (T->rchild!=NULL && T->lchild==NULL))return Degree1(T->lchild)+Degree1(T->rchild)+1;else return Degree1(T->lchild)+Degree1(T->rchild);
}

统计度为2的节点

int Degree2(BiTree T){if(T==NULL) return 0;if(T->rchild!=NULL && T->lchild!=NULL )	return  Degree2(T->lchild)+Degree2(T->rchild)+1;else return Degree2(T->lchild)+Degree2(T->rchild);
}

计算树的高度

int BtDepth(BiTree T){if(T==NULL) return 0;int ldep = BtDepth(T->lchild);int rdep = BtDepth(T->rchild);if(ldep > rdep) return ldep+1;else return rdep+1;
}

3.主函数示例（功能测试）

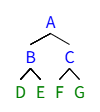
int main() {BiTree T1;InitBiTree(T1);printf("请输入二叉树的先序序列（以#表示空节点）：");CreateBiTree(T1);  // 构建二叉树printf("中序遍历结果：");InOrder2(T1);      // 测试中序非递归遍历printf("\n层序遍历结果：");LevelOrder(T1);    // 测试层序遍历printf("\n叶子节点个数：%d", Degree0(T1));printf("\n度为1,2的节点个数分别为：%d,%d", Degree1(T1),Degree2(T1));printf("\n树的高度：%d", BtDepth(T1));DestroyBiTree(T1);  // 销毁二叉树，释放内存return 0;
}

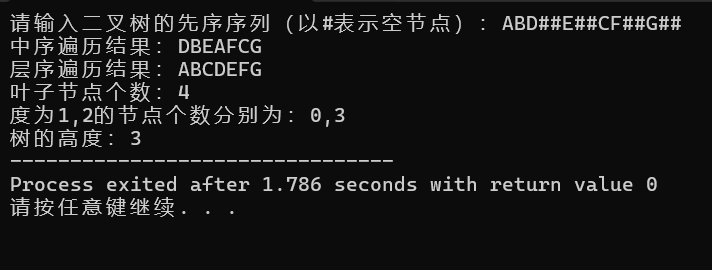
三、总结与提示

时间复杂度分析：所有遍历算法的时间复杂度均为O(n)，其中n为节点数量
空间复杂度分析：
- 递归遍历：O(h)，h为树高（递归栈空间）
- 非递归中序遍历：O(h)（栈空间）
- 层序遍历：O(w)，w为树的最大宽度（队列空间）
实用技巧：
- 先序+中序或后序+中序可以唯一确定一棵二叉树
- 递归算法简洁但可能存在栈溢出风险，非递归算法更安全
- 销毁二叉树务必使用后序遍历，避免内存泄漏