LeetCode Hot 100 Python (11~20)
滑动窗口最大值:困难
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
| 示例 | 1 | 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 输入 | nums = [1,3,-1,-3,5,3,6,7], k = 3 | nums = [1], k = 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 输出 | [3,3,5,5,6,7] | [1] | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 解释 |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
单调队列套路
- 入(元素进入队尾,同时维护队列单调性)
- 出(元素离开队首)
- 记录/维护答案(根据队首)
这个解法使用双端队列维护一个单调递减的队列,确保队首始终是当前窗口的最大值。具体步骤如下:
- 入队操作:遍历数组时,将当前元素与队尾元素比较,若当前元素更大,则弹出队尾元素,直到队列为空或队尾元素更大。然后将当前元素索引加入队尾,保持队列的单调递减性。
- 出队操作:检查队首元素是否超出当前窗口范围(即索引差≥k),若超出则弹出队首元素,确保队列中的元素都在窗口内。
- 记录结果:当窗口形成(i≥k-1)时,队首元素即为当前窗口的最大值,将其加入结果列表。
class Solution:def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:ans = []q = deque() # 双端队列for i, x in enumerate(nums):# 1. 入while q and nums[q[-1]] <= x:q.pop() # 维护 q 的单调性q.append(i) # 入队# 2. 出if i - q[0] >= k: # 队首已经离开窗口了q.popleft()# 3. 记录答案if i >= k - 1:# 由于队首到队尾单调递减,所以窗口最大值就是队首ans.append(nums[q[0]])return ans
| 时间复杂度 | 空间复杂度 |
| O(n) | O(min(k,U)) |
| 其中 n 为 nums 的长度。由于每个下标至多入队出队各一次,所以二重循环的循环次数是 O(n) 的 | 其中 U 是 nums 中的不同元素个数(本题至多为 20001)。双端队列至多有 k 个元素,同时又没有重复元素,所以也至多有 U 个元素,所以空间复杂度为 O(min(k,U))。返回值的空间不计入 |
最小覆盖子串:困难
给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串,则返回空字符串 "" 。
注意:对于 t 中重复字符,我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量;如果 s 中存在这样的子串,我们保证它是唯一的答案。
| 示例 | 1 | 2 | 3 |
| 输入 | s = "ADOBECODEBANC" t = "ABC" | s = "a", t = "a" | s = "a", t = "aa" |
| 输出 | "BANC" | "a" | "" |
| 解释 | 最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。 | 整个字符串 s 是最小覆盖子串。 | t 中两个字符 'a' 均应包含在 s 的子串中,因此没有符合条件的子字符串,返回空字符串。 |
「涵盖」看示例 1,s 的子串 BANC 中每个字母的出现次数,都大于等于 t=ABC 中每个字母的出现次数,这就叫涵盖。
滑动窗口怎么滑
我们枚举 s 子串的右端点 right(子串最后一个字母的下标),如果子串涵盖 t,就不断移动左端点 left 直到不涵盖为止。在移动过程中更新最短子串的左右端点。具体来说:
- 初始化 ansLeft=−1, ansRight=m,用来记录最短子串的左右端点,其中 m 是 s 的长度。
- 用一个哈希表(或者数组)cntT 统计 t 中每个字母的出现次数。
- 初始化 left=0,以及一个空哈希表(或者数组)cntS,用来统计 s 子串中每个字母的出现次数。
- 遍历 s,设当前枚举的子串右端点为 right,把 s[right] 的出现次数加一。
- 遍历 cntS 中的每个字母及其出现次数,如果出现次数都大于等于 cntT 中的字母出现次数:
- 如果 right−left<ansRight−ansLeft,说明我们找到了更短的子串,更新 ansLeft=left, ansRight=right。
- 把 s[left] 的出现次数减一。
- 左端点右移,即 left 加一。
- 重复上述三步,直到 cntS 有字母的出现次数小于 cntT 中该字母的出现次数为止。
- 最后,如果 ansLeft<0,说明没有找到符合要求的子串,返回空字符串,否则返回下标 ansLeft 到下标 ansRight 之间的子串。
由于本题大写字母和小写字母都有,为了方便,代码实现时可以直接创建大小为 128 的数组,保证所有 ASCII 字符都可以统计。
法一:
# 请选择 Python3 提交代码,而不是 Python
class Solution:def minWindow(self, s: str, t: str) -> str:ans_left, ans_right = -1, len(s)cnt_s = Counter() # s 子串字母的出现次数cnt_t = Counter(t) # t 中字母的出现次数left = 0for right, c in enumerate(s): # 移动子串右端点cnt_s[c] += 1 # 右端点字母移入子串while cnt_s >= cnt_t: # 涵盖if right - left < ans_right - ans_left: # 找到更短的子串ans_left, ans_right = left, right # 记录此时的左右端点cnt_s[s[left]] -= 1 # 左端点字母移出子串left += 1return "" if ans_left < 0 else s[ans_left: ans_right + 1]
| 时间复杂度 | 空间复杂度 |
| O(∣Σ∣m+n) | O(∣Σ∣) |
| 其中 m 为 s 的长度,n 为 t 的长度,∣Σ∣ 为字符集合的大小,本题字符均为英文字母,所以 ∣Σ∣=52。注意 left 只会增加不会减少,left 每增加一次,我们就花费 O(∣Σ∣) 的时间。因为 left 至多增加 m 次,所以二重循环的时间复杂度为 O(∣Σ∣m),再算上统计 t 字母出现次数的时间 O(n),总的时间复杂度为 O(∣Σ∣m+n) | 如果创建了大小为 128 的数组,则 ∣Σ∣=128 |
法二:优化
上面的代码每次都要花费 O(∣Σ∣) 的时间去判断是否涵盖,能不能优化到 O(1) 呢?可以用一个变量 less 维护目前子串中有 less 种字母的出现次数小于 t 中字母的出现次数。具体来说(注意下面算法中的 less 变量):
- 初始化 ansLeft=−1, ansRight=m,用来记录最短子串的左右端点,其中 m 是 s 的长度。
- 用一个哈希表(或者数组)cntT 统计 t 中每个字母的出现次数。
- 初始化 left=0,以及一个空哈希表(或者数组)cntS,用来统计 s 子串中每个字母的出现次数。
- 初始化 less 为 t 中的不同字母个数。
- 遍历 s,设当前枚举的子串右端点为 right,把字母 c=s[right] 的出现次数加一。加一后,如果 cntS[c]=cntT[c],说明 c 的出现次数满足要求,把 less 减一。
- 如果 less=0,说明 cntS 中的每个字母及其出现次数都大于等于 cntT 中的字母出现次数,那么:
- 如果 right−left<ansRight−ansLeft,说明我们找到了更短的子串,更新 ansLeft=left, ansRight=right。
- 把字母 x=s[left] 的出现次数减一。减一前,如果 cntS[x]=cntT[x],说明 x 的出现次数不满足要求,把 less 加一。
- 左端点右移,即 left 加一。
- 重复上述三步,直到 less>0,即 cntS 有字母的出现次数小于 cntT 中该字母的出现次数为止。
- 最后,如果 ansLeft<0,说明没有找到符合要求的子串,返回空字符串,否则返回下标 ansLeft 到下标 ansRight 之间的子串。
代码实现时,可以把 cntS 和 cntT 合并成一个 cnt,定义:cnt[x]=cntT[x]−cntS[x]
如果 cnt[x]=0,就意味着窗口内字母 x 的出现次数和 t 的一样多。
class Solution:def minWindow(self, s: str, t: str) -> str:ans_left, ans_right = -1, len(s)cnt = defaultdict(int) # 比 Counter 更快for c in t:cnt[c] += 1less = len(cnt) # 有 less 种字母的出现次数 < t 中的字母出现次数left = 0for right, c in enumerate(s): # 移动子串右端点cnt[c] -= 1 # 右端点字母移入子串if cnt[c] == 0:# 原来窗口内 c 的出现次数比 t 的少,现在一样多less -= 1while less == 0: # 涵盖:所有字母的出现次数都是 >=if right - left < ans_right - ans_left: # 找到更短的子串ans_left, ans_right = left, right # 记录此时的左右端点x = s[left] # 左端点字母if cnt[x] == 0:# x 移出窗口之前,检查出现次数,# 如果窗口内 x 的出现次数和 t 一样,# 那么 x 移出窗口后,窗口内 x 的出现次数比 t 的少less += 1cnt[x] += 1 # 左端点字母移出子串left += 1return "" if ans_left < 0 else s[ans_left: ans_right + 1]
| 时间复杂度 | 空间复杂度 |
| O(m+n) 或 O(m+n+∣Σ∣) | O(∣Σ∣) |
| 其中 m 为 s 的长度,n 为 t 的长度,∣Σ∣=128。注意 left 只会增加不会减少,二重循环的时间复杂度为 O(m)。使用哈希表写法的时间复杂度为 O(m+n),数组写法的时间复杂度为 O(m+n+∣Σ∣)。 | 无论 m 和 n 有多大,额外空间都不会超过 O(∣Σ∣)。 |
最大子数组和:中等
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组是数组中的一个连续部分。
| 示例 | 1 | 2 | 3 |
| 输入 | nums = [-2,1,-3,4,-1,2,1,-5,4] | nums = [1] | nums = [5,4,-1,7,8] |
| 输出 | "6 | 1 | 23 |
| 解释 | 连续子数组 [4,-1,2,1] 的和最大,为 6 |
法一:前缀和 + 贪心
前置知识:前缀和
由于子数组的元素和等于两个前缀和的差,所以求出 nums 的前缀和,问题就变成 121. 买卖股票的最佳时机 了。本题子数组不能为空,相当于一定要交易一次。
我们可以一边遍历数组计算前缀和,一边维护前缀和的最小值(相当于股票最低价格),用当前的前缀和(卖出价格)减去前缀和的最小值(买入价格),就得到了以当前元素结尾的子数组和的最大值(利润),用它来更新答案的最大值(最大利润)。
请注意,由于题目要求子数组不能为空,应当先计算前缀和-最小前缀和,再更新最小前缀和。相当于不能在同一天买入股票又卖出股票。
如果先更新最小前缀和,再计算前缀和-最小前缀和,就会把空数组的元素和 0 算入答案。
示例 1 [−2,1,−3,4,−1,2,1,−5,4] 的计算流程如下,可以对照代码理解。注意计算顺序。
| 元素值 | 前缀和 | 最小前缀和 | 前缀和-最小前缀和 |
| −2 | −2 | 0 | −2 |
| 1 | −1 | −2 | 1 |
| −3 | −4 | −2 | −2 |
| 4 | 0 | −4 | 4 |
| −1 | −1 | −4 | 3 |
| 2 | 1 | −4 | 5 |
| 1 | 2 | −4 | 6 |
| −5 | −3 | −4 | 1 |
| 4 | 1 | −4 | 5 |
前缀和-最小前缀和的最大值等于 6,即为答案。
class Solution:def maxSubArray(self, nums: List[int]) -> int:ans = -infmin_pre_sum = pre_sum = 0for x in nums:pre_sum += x # 当前的前缀和ans = max(ans, pre_sum - min_pre_sum) # 减去前缀和的最小值min_pre_sum = min(min_pre_sum, pre_sum) # 维护前缀和的最小值return ans
| 时间复杂度 | 空间复杂度 |
| O(n) | O(1) |
| 其中 n 为 nums 的长度 | 仅用到若干额外变量 |
法二:动态规划
定义 f[i] 表示以 nums[i] 结尾的最大子数组和。
分类讨论:
- nums[i] 单独组成一个子数组,那么 f[i]=nums[i]。
- nums[i] 和前面的子数组拼起来,也就是在以 nums[i−1] 结尾的最大子数组和之后添加 nums[i],那么 f[i]=f[i−1]+nums[i]。
两种情况取最大值,得
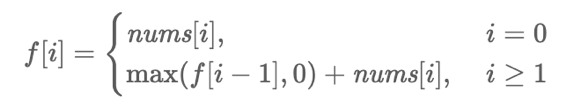
简单地说,如果 nums[i] 左边的子数组元素和是负的,就不用和左边的子数组拼在一起了。
答案为 max(f)。
⚠注意:答案不是 f[n−1],这仅仅表示以 nums[n−1] 结尾的最大子数组和。或者说 f[n−1] 意味着 nums[n−1] 一定要选,但这不一定正确。
class Solution:def maxSubArray(self, nums: List[int]) -> int:f = [0] * len(nums)f[0] = nums[0]for i in range(1, len(nums)):f[i] = max(f[i - 1], 0) + nums[i]return max(f)
空间优化
由于计算 f[i] 只会用到 f[i−1],不会用到更早的状态,所以可以用一个变量滚动计算。具体请看视频讲解 动态规划入门:从记忆化搜索到递推。
状态转移方程简化为:f=max(f,0)+nums[i](f 可以初始化成 0 或者任意负数)。
class Solution:def maxSubArray(self, nums: List[int]) -> int:ans = -inf # 注意答案可以是负数,不能初始化成 0f = 0for x in nums:f = max(f, 0) + xans = max(ans, f)return ans
| 时间复杂度 | 空间复杂度 |
| O(n) | O(1) |
| 其中 n 为 nums 的长度 | 仅用到若干额外变量 |
合并区间:中等
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
| 示例 | 1 | 2 |
| 输入 | intervals = [[1,3],[2,6],[8,10],[15,18]] | intervals = [[1,4],[4,5]] |
| 输出 | [[1,6],[8,10],[15,18]] | [[1,5]] |
| 解释 | 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6] | 区间 [1,4] 和 [4,5] 可被视为重叠区间 |
以示例 1 为例,我们有 [1,3],[2,6],[8,10],[15,18] 这四个区间。
为方便合并,把区间按照左端点从小到大排序(示例 1 已经按照左端点排序了)。
排序后,我们就知道了第一个合并区间的左端点,即 intervals[0][0]=1。
第一个合并区间的右端点是多少?目前只知道其 ≥intervals[0][1]=3,但具体是多少现在还不确定,得向右遍历。
具体算法如下:
把 intervals[0] 加入答案。注意,答案的最后一个区间表示当前正在合并的区间。
遍历到 intervals[1]=[2,6],由于左端点 2 不超过当前合并区间的右端点 3,可以合并。由于右端点 6>3,那么更新当前合并区间的右端点为 6。注意,由于我们已经按照左端点排序,所以 intervals[1] 的左端点 2 必然大于等于合并区间的左端点,所以无需更新当前合并区间的左端点。
遍历到 intervals[2]=[8,10],由于左端点 8 大于当前合并区间的右端点 6,无法合并(两个区间不相交)。再次利用区间按照左端点排序的性质,更后面的区间的左端点也大于 6,无法与当前合并区间相交,所以当前合并区间 [1,6] 就固定下来了,把新的合并区间 [8,10] 加入答案。
遍历到 intervals[3]=[15,18],由于左端点 15 大于当前合并区间的右端点 10,无法合并(两个区间不相交),我们找到了一个新的合并区间 [15,18] 加入答案。
上述算法同时说明,按照左端点排序后,合并的区间一定是 intervals 中的连续子数组。
能不能按照右端点排序?可以,但是需要倒着遍历 intervals 数组。如果正着遍历,比如 [1,2],[4,5],[1,6] 这三个区间,正确答案是合并成 [1,6],但正着遍历到 [4,5] 这个区间时,无法知道 [4,5] 能否和 [1,2] 彻底断开。但按左端点排序的话,我们就知道这是不会断开的,会和之前的区间合并在一起。
class Solution:def merge(self, intervals: List[List[int]]) -> List[List[int]]:intervals.sort(key=lambda p: p[0]) # 按照左端点从小到大排序ans = []for p in intervals:if ans and p[0] <= ans[-1][1]: # 可以合并ans[-1][1] = max(ans[-1][1], p[1]) # 更新右端点最大值else: # 不相交,无法合并ans.append(p) # 新的合并区间return ans
| 时间复杂度 | 空间复杂度 |
| O(nlogn) | O(1) |
| 其中 n 是 intervals 的长度,瓶颈在排序上 | 排序的栈开销和返回值不计入 |
轮转数组:中等
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
| 示例 | 1 | 2 |
| 输入 | nums = [1,2,3,4,5,6,7], k = 3 | nums = [-1,-100,3,99], k = 2 |
| 输出 | [5,6,7,1,2,3,4] | [3,99,-1,-100] |
| 解释 | 向右轮转 1 步: [7,1,2,3,4,5,6] 向右轮转 2 步: [6,7,1,2,3,4,5] 向右轮转 3 步: [5,6,7,1,2,3,4] | 向右轮转 1 步: [99,-1,-100,3] 向右轮转 2 步: [3,99,-1,-100] |
例子
把 [1,2,3,4,5,6,7] 变成 [5,6,7,1,2,3,4],首先要保证 5,6,7 在 1,2,3,4 前面,这可以通过反转整个数组做到。
反转后数组变成 [7,6,5,4,3,2,1],对比最终目标可以发现,前三个数需要反转,后四个数需要反转,这样就得到了 [5,6,7,1,2,3,4]。
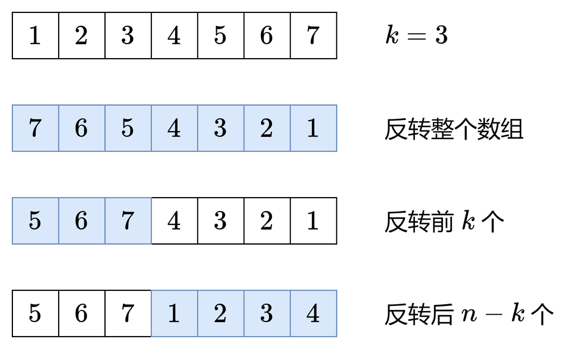
一般化
这里假设 0≤k<n,对于 k≥n 的情况,可以转换成 0≤k<n 的情况(证明见后文)。
设 nums=A+B,其中 A 是 nums 的前 n−k 个数,B 是后 k 个数。在上例中,A=[1,2,3,4],B=[5,6,7]。
题目要求把 A+B 变成 B+A,这可以用三次反转实现:
- 把 nums 反转,我们得到了 rev(B)+rev(A),其中 rev(A) 表示数组 A 反转后的结果。在上例中,rev(B)+rev(A)=[7,6,5]+[4,3,2,1]。
- 单独反转 rev(B),因为一个数组反转两次是不变的,所以 rev(rev(B))=B,我们得到了 B。
- 单独反转 rev(A),得到 A。
- 现在数组变成 B+A。在上例中,B+A=[5,6,7]+[1,2,3,4],这正是我们想要的结果。
正确性证明
向右轮转 k 个位置后,下标 i 的元素移动到下标 (i+k)modn 上,其中 n 是 nums 的长度。
下面证明上述方法(三次反转)的正确性。
假设 0≤k<n,也就是 0≤k≤n−1,分类讨论:
- 如果 n−k≤i≤n−1,那么第一次反转(整个数组的反转)会把下标 i 的元素交换到下标 n−1−i 上(注意 0≤n−1−i≤k−1,在第二次反转的范围中),第二次反转会把下标 n−1−i 的元素交换到下标 k−1−(n−1−i)=i+k−n 上。根据 n−k≤i≤n−1 可得 0≤i+k−n≤k−1,所以 i+k−n=(i+k)modn,符合题目要求。
- 如果 0≤i≤n−k−1,那么第一次反转(整个数组的反转)会把下标 i 的元素交换到下标 n−1−i 上(注意 k≤n−1−i≤n−1,在第三次反转的范围中),第三次反转会把下标 n−1−i 的元素交换到下标 k+n−1−(n−1−i)=i+k 上(注*)。根据 0≤i≤n−k−1 可得 k≤i+k≤n−1,所以 i+k=(i+k)modn,符合题目要求。
对于 k≥n 的情况,由于轮转 n 次等同于没有轮转,轮转 n+1 等同于轮转 1 次……依此类推,轮转 k 次等同于轮转 kmodn 次。由于 0≤kmodn≤n−1,所以 k≥n 的情况也是正确的。
综上所述,对于任意非负整数 k,按照图中三次反转的方法,可以把下标 i 的元素移动到下标 (i+k)modn 上。
注:对于下标区间 [L,R] 的反转,由于 i=L 会反转到 R,i=L+1 会反转到 R−1,i=L+2 会反转到 R−2,依此类推,下标 i 和反转后的位置 j 满足 i+j=L+R,所以 i 会反转到 L+R−i。
# 注:请勿使用切片,会产生额外空间
class Solution:def rotate(self, nums: List[int], k: int) -> None:def reverse(i: int, j: int) -> None:while i < j:nums[i], nums[j] = nums[j], nums[i]i += 1j -= 1n = len(nums)k %= n # 轮转 k 次等于轮转 k % n 次reverse(0, n - 1)reverse(0, k - 1)reverse(k, n - 1)
| 时间复杂度 | 空间复杂度 |
| O(n) | O(1) |
| 其中 n 是 nums 的长度 |
除自身以外数组的乘积:中等
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请 不要使用除法,且在 O(n) 时间复杂度内完成此题。
| 示例 | 1 | 2 |
| 输入 | nums = [1,2,3,4] | nums = [-1,1,0,-3,3] |
| 输出 | [24,12,8,6] | [0,0,9,0,0] |
answer[i] 等于 nums 中除了 nums[i] 之外其余各元素的乘积。换句话说,如果知道了 i 左边所有数的乘积,以及 i 右边所有数的乘积,就可以算出 answer[i]。
于是:
- 定义 pre[i] 表示从 nums[0] 到 nums[i−1] 的乘积。
- 定义 suf[i] 表示从 nums[i+1] 到 nums[n−1] 的乘积。
我们可以先计算出从 nums[0] 到 nums[i−2] 的乘积 pre[i−1],再乘上 nums[i−1],就得到了 pre[i],即:pre[i]=pre[i−1]⋅nums[i−1]。
同理有:suf[i]=suf[i+1]⋅nums[i+1]。
初始值:pre[0]=suf[n−1]=1。按照上文的定义,pre[0] 和 suf[n−1] 都是空子数组的元素乘积,我们规定这是 1,因为 1 乘以任何数 x 都等于 x,这样可以方便递推计算 pre[1],suf[n−2] 等。
算出 pre 数组和 suf 数组后,有:answer[i]=pre[i]⋅suf[i]。
class Solution:def productExceptSelf(self, nums: List[int]) -> List[int]:n = len(nums)pre = [1] * nfor i in range(1, n):pre[i] = pre[i - 1] * nums[i - 1]suf = [1] * nfor i in range(n - 2, -1, -1):suf[i] = suf[i + 1] * nums[i + 1]return [p * s for p, s in zip(pre, suf)]
| 时间复杂度 | 空间复杂度 |
| O(n) | O(n) |
| 其中 n 是 nums 的长度 |
优化:不使用额外空间
先计算 suf,然后一边计算 pre,一边把 pre 直接乘到 suf[i] 中。最后返回 suf。
题目说「输出数组不被视为额外空间」,所以该做法的空间复杂度为 O(1)。此外,这种做法比上面少遍历了一次。
class Solution:def productExceptSelf(self, nums: List[int]) -> List[int]:n = len(nums)suf = [1] * nfor i in range(n - 2, -1, -1):suf[i] = suf[i + 1] * nums[i + 1]pre = 1for i, x in enumerate(nums):# 此时 pre 为 nums[0] 到 nums[i-1] 的乘积,直接乘到 suf[i] 中suf[i] *= prepre *= xreturn suf
| 时间复杂度 | 空间复杂度 |
| O(n) | O(1) |
| 其中 n 是 nums 的长度 | 返回值不计入 |
缺失的第一个正数:困难
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
| 示例 | 1 | 2 | 3 |
| 输入 | nums = [1,2,0] | nums = [3,4,-1,1] | nums = [7,8,9,11,12] |
| 输出 | 3 | 2 | 1 |
| 解释 | 范围 [1,2] 中的数字都在数组中 | 1 在数组中,但 2 没有 | 最小的正数 1 没有出现 |
思路
想象有一个教室,座位从左到右编号为 1 到 n。
有 n 个学生坐在教室的座位上,把 nums[i] 当作坐在第 i 个座位上的学生的学号。我们要做的事情,就是让学号在 1 到 n 中的学生,都坐到编号与自己学号相同的座位上。学号不在 [1,n] 中的学生可以忽略。
学生们交换座位后,从左到右看,第一个学号与座位编号不匹配的学生,其座位编号就是答案。
特别地,如果所有学生都坐在正确的座位上,那么答案是 n+1。
第一个例子
为方便描述思路,假设数组的下标是从 1 开始的。假设 nums=[2,3,1]。
- 从 nums[1] 开始。这个座位上的学生,学号是 2,他应当坐在 nums[2] 上,所以他和 nums[2] 交换。交换后 nums=[3,2,1]。
- 仍然看 nums[1],这个座位上的学生,学号是 3,他应当坐在 nums[3] 上,所以他和 nums[3] 交换。交换后 nums=[1,2,3]。
- 仍然看 nums[1],这个座位上的学生,学号是 1,他坐在正确的座位上。
- 向后遍历,nums[2]=2,他坐在正确的座位上。
- 向后遍历,nums[3]=3,他坐在正确的座位上。
- 换座位过程结束。
- 再次遍历 nums,发现 nums[i]=i 都满足,说明数组中 1,2,3 都有,所以缺失的第一个正数是 4。
第二个例子
假设 nums=[3,4,−1,1],这是题目中的示例 2。
- 从 nums[1] 开始。这个座位上的学生,学号是 3,他应当坐在 nums[3] 上,所以他和 nums[3] 交换。交换后 nums=[−1,4,3,1]。
- 仍然看 nums[1],这个座位上的学生,学号是 −1,忽略。
- 向后遍历,nums[2]=4,他应当坐在 nums[4] 上,所以他和 nums[4] 交换。交换后 nums=[−1,1,3,4]。
- 仍然看 nums[2]=1,他应当坐在 nums[1] 上,所以他和 nums[1] 交换。交换后 nums=[1,−1,3,4]。
- 仍然看 nums[2],这个座位上的学生,学号是 −1,忽略。
- 向后遍历,nums[3]=3,他坐在正确的座位上。
- 向后遍历,nums[4]=4,他坐在正确的座位上。
- 换座位过程结束。
- 再次遍历 nums,发现 nums[2]=−1≠2,说明教室中没有学号为 2 的学生(否则他会坐在 nums[2] 上),所以答案是 2。
第三个例子
注意 nums 中可能有重复元素。在这种情况下,算法仍然是正确的吗?
假设 nums=[1,1,2]。
- 从 nums[1] 开始。这个座位上的学生坐在正确的座位上。
- 继续遍历,nums[2]=1,这是 1 号学生的影分身。由于 1 号学生的真身已经坐在正确的座位上,我们可以在第二次遍历中知道「数组中有 1」这个信息,所以可以忽略 nums[2],向后遍历。
- nums[3]=2,他应当坐在 nums[2] 上,所以他和 nums[2] 交换。交换后 nums=[1,2,1]。
- 仍然看 nums[3]=1,同样地,由于 1 号学生已经坐在正确的座位上,所以可以忽略 nums[3]。
- 换座位过程结束。
- 再次遍历 nums,发现 nums[3]=1≠3,说明教室中没有学号为 3 的学生,所以答案是 3。
细节
判断「学生是否坐在正确的座位上」,能用 nums[i]=i 判断吗?注意有影分身(重复元素)。
在第三个例子中,虽然 nums[2]=1≠2,但由于 nums[nums[2]]=nums[1]=1,所以 nums[2] 是个影分身,并且其真身坐在了正确的座位上,所以可以忽略 nums[2],向后遍历。注意这种情况是不能交换的,因为 nums[2]=nums[1],交换后 nums=[1,1,2] 是不变的,这会导致死循环。
为避免死循环,可以改成判断 nums[2] 和 nums[nums[2]] 是不是一样的。如果一样,就不执行交换,继续向后遍历。
一般地,为了兼容「当前学生是真身,坐在正确的座位上」和「当前学生是影分身,且其真身坐在正确的座位上」两种情况,我们可以把 i=nums[i] 套一层 nums,用 nums[i]=nums[nums[i]] 判断。
- 无论「当前学生是真身,坐在正确的座位上」还是「当前学生是影分身,且其真身坐在正确的座位上」,上式都是成立的。
- 如果「当前学生是真身,不坐在正确的座位上」,那么上式左边是当前学生的学号,右边是要交换的学生的学号。
- 如果「当前学生是影分身,且其真身不坐在正确的座位上」,那么上式左边是当前学生的学号,右边是要交换的学生的学号。虽然是用影分身交换的,但交换后,可以认为真身已经坐在了正确的座位上。
代码实现时,由于 nums 的下标是从 0 开始的,通过学号访问下标,要把学号减一。
class Solution:def firstMissingPositive(self, nums: list[int]) -> int:n = len(nums)for i in range(n):# 如果当前学生的学号在 [1,n] 中,但(真身)没有坐在正确的座位上while 1 <= nums[i] <= n and nums[i] != nums[nums[i] - 1]:# 那么就交换 nums[i] 和 nums[j],其中 j 是 i 的学号j = nums[i] - 1 # 减一是因为数组下标从 0 开始nums[i], nums[j] = nums[j], nums[i]# 找第一个学号与座位编号不匹配的学生for i in range(n):if nums[i] != i + 1:return i + 1# 所有学生都坐在正确的座位上return n + 1
| 时间复杂度 | 空间复杂度 |
| O(n) | O(1) |
| 其中 n 是 nums 的长度。虽然我们写了个二重循环,但每次交换都会把一个学生换到正确的座位上,所以总交换次数至多为 n,所以内层循环的总循环次数是 O(n) 的,所以时间复杂度是 O(n) |
矩阵置零:中等
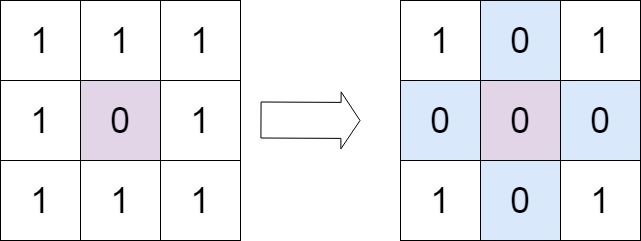
给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。
| 示例 | 1 | 2 |
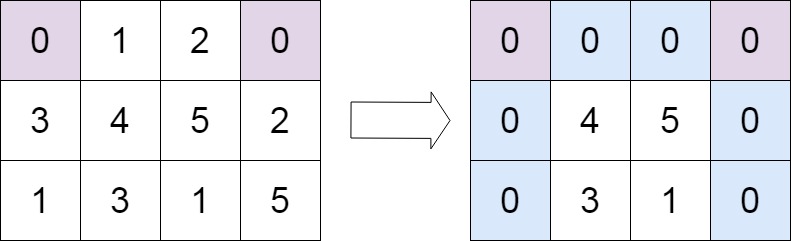
| 输入 | matrix = [[1,1,1],[1,0,1],[1,1,1]] | matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]] |
| 输出 | [[1,0,1],[0,0,0],[1,0,1]] | [[0,0,0,0],[0,4,5,0],[0,3,1,0]] |
|
|
|
法一: 用 O(m+n)额外空间
这个解法通过记录需要置零的行和列,然后遍历矩阵进行置零操作。具体步骤如下:
- 记录需要置零的行和列:遍历矩阵,当遇到元素为0时,记录其行号和列号到集合 row_zero 和 col_zero 中。
- 置零操作:再次遍历矩阵,如果当前行或列在 row_zero 或 col_zero 中,则将当前元素置零。
class Solution:def setZeroes(self, matrix: List[List[int]]) -> None:"""Do not return anything, modify matrix in-place instead."""row = len(matrix)col = len(matrix[0])row_zero = set()col_zero = set()for i in range(row):for j in range(col):if matrix[i][j] == 0:row_zero.add(i)col_zero.add(j)for i in range(row):for j in range(col):if i in row_zero or j in col_zero:matrix[i][j] = 0
| 时间复杂度 | 空间复杂度 |
| O(mn) | O(m+n) |
| 其中 m 和 n 分别是矩阵的行数和列数 |
法二: 用O(1)空间
这个解法通过使用矩阵的第一行和第一列来记录需要置零的行和列,从而优化了空间复杂度。具体步骤如下:
- 检查第一行和第一列是否有零:分别遍历第一行和第一列,记录是否存在零,以便后续处理。
- 使用第一行和第一列作为标志位:遍历矩阵的其余部分,如果某个元素为零,则将该元素所在行的第一个元素和所在列的第一个元素置零。
- 根据标志位置零:再次遍历矩阵的其余部分,如果某行的第一个元素或某列的第一个元素为零,则将该元素置零。
- 处理第一行和第一列:根据之前的记录,如果第一行或第一列原本有零,则将整行或整列置零。
class Solution:def setZeroes(self, matrix: List[List[int]]) -> None:"""Do not return anything, modify matrix in-place instead."""row = len(matrix)col = len(matrix[0])row0_flag = Falsecol0_flag = False# 找第一行是否有0for j in range(col):if matrix[0][j] == 0:row0_flag = Truebreak# 第一列是否有0for i in range(row):if matrix[i][0] == 0:col0_flag = Truebreak# 把第一行或者第一列作为 标志位for i in range(1, row):for j in range(1, col):if matrix[i][j] == 0:matrix[i][0] = matrix[0][j] = 0#print(matrix)# 置0for i in range(1, row):for j in range(1, col):if matrix[i][0] == 0 or matrix[0][j] == 0:matrix[i][j] = 0if row0_flag:for j in range(col):matrix[0][j] = 0if col0_flag:for i in range(row):matrix[i][0] = 0
简化版
class Solution:def setZeroes(self, matrix: List[List[int]]) -> None:"""Do not return anything, modify matrix in-place instead."""flag_col = Falserow = len(matrix)col = len(matrix[0])for i in range(row):if matrix[i][0] == 0: flag_col = Truefor j in range(1,col):if matrix[i][j] == 0:matrix[i][0] = matrix[0][j] = 0for i in range(row - 1, -1, -1):for j in range(col - 1, 0, -1):if matrix[i][0] == 0 or matrix[0][j] == 0:matrix[i][j] = 0if flag_col == True: matrix[i][0] = 0
| 时间复杂度 | 空间复杂度 |
| O(mn) | O(1) |
| 其中 m 和 n 分别是矩阵的行数和列数 |
螺旋矩阵:中等
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
| 示例 | 1 | 2 |
| 输入 | matrix = [[1,2,3],[4,5,6],[7,8,9]] | matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]] |
| 输出 | [1,2,3,6,9,8,7,4,5] | [1,2,3,4,8,12,11,10,9,5,6,7] |
|
|
|
总体思路
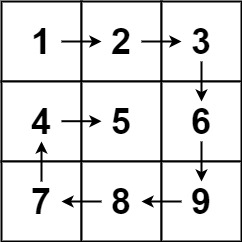
根据题意,我们从左上角 (0,0) 出发,按照「右下左上」的顺序前进:
- 首先向右走,如果到达矩阵边界,则向右转 90o,前进方向变为向下。
- 然后向下走,如果到达矩阵边界,则向右转 90o,前进方向变为向左。
- 然后向左走,如果到达矩阵边界,则向右转 90o,前进方向变为向上。
- 然后向上走,先从 7 走到 4,然后从 4 准备向上走,但上面的 1 是一个已经访问过的数字,那么向右转 90o,前进方向变为向右。
- 重复上述过程,直到答案的长度为 mn。
法一:标记
对于已经访问过的数字,可将其标记为 ∞ 或者空,从而避免重复访问。
用一个长为 4 的方向数组 DIRS=[(0,1),(1,0),(0,−1),(−1,0)] 分别表示右下左上 4 个方向。同时用一个下标 di 表示当前方向,初始值为 0。
每次移动,相当于把行号增加 DIRS[di][0],把列号增加 DIRS[di][1]。
向右转90o,相当于把 di 增加 1,但在 di=3 时要回到 di=0。两种情况合二为一,把 di 更新为 (di+1)mod4。
DIRS = (0, 1), (1, 0), (0, -1), (-1, 0) # 右下左上class Solution:def spiralOrder(self, matrix: List[List[int]]) -> List[int]:m, n = len(matrix), len(matrix[0])ans = []i = j = di = 0for _ in range(m * n): # 一共走 mn 步ans.append(matrix[i][j])matrix[i][j] = None # 标记,表示已经访问过(已经加入答案)x, y = i + DIRS[di][0], j + DIRS[di][1] # 下一步的位置# 如果 (x, y) 出界或者已经访问过if x < 0 or x >= m or y < 0 or y >= n or matrix[x][y] is None:di = (di + 1) % 4 # 右转 90°i += DIRS[di][0]j += DIRS[di][1] # 走一步return ans
| 时间复杂度 | 空间复杂度 |
| O(mn) | O(1) |
| 其中 m 和 n 分别是矩阵的行数和列数 |
法二:不标记
上面的做法需要修改 matrix,能否不修改呢?
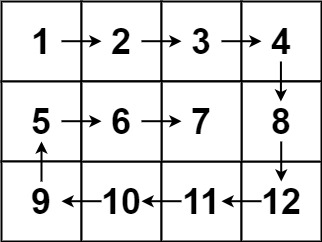
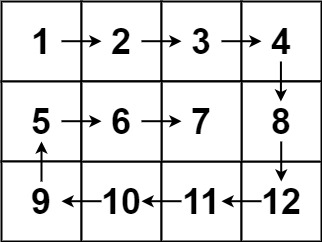
示例 2 这 12 个数字,可以分为以下 5 组:
- 1→2→3→4
- 8→12
- 11→10→9
- 5
- 6→7
其中第 1,3,5 组都是向右或者向左走的,长度依次为 4,3,2,这是一个从 n=4 开始的逐渐递减的序列。
其中第 2,4 组都是向下或者向上走的,长度依次为 2,1,这是一个从 m−1=2 开始的逐渐递减的序列。
由于走的步数是有规律的,我们可以精确地控制在每个方向上要走多少步,无需判断是否出界、是否重复访问:
- 从 (0,−1) 开始。
- 一开始,向右走 n 步,每次先走一步,再把数字加入答案。走 n 步即 1→2→3→4,矩阵第一排的数都加入了答案。
- 然后向下走 m−1 步,即 8→12。
- 然后向左走 n−1 步,即 11→10→9。
- 然后向上走 m−2 步,即 5。
- 然后向右走 n−2 步,即 6→7。
- 重复上述过程,直到答案的长度等于 mn。
代码实现时,可以这样简化代码:
- 一开始走 n 步。
- 把 n,m 分别更新为 m−1,n,这样下一轮循环又可以走 n 步(相当于走了 m−1 步),无需修改其他逻辑。
- 把 n,m 分别更新为 m−1,n,这样下一轮循环又可以走 n 步(相当于走了 n−1 步)。
- 把 n,m 分别更新为 m−1,n,这样下一轮循环又可以走 n 步(相当于走了 m−2 步)。
- 依此类推,每次只需把 n,m 分别更新为 m−1,n 即可。
如何说明这个规律的正确性?在上文的例子中,我们把示例 2 分成了 5 组。一般地,每 4 组,我们会把矩阵最外面一圈去掉(就像剥洋葱),矩阵的行数会减少 2,列数会减少 2。所以行列的减少是有规律的。
DIRS = (0, 1), (1, 0), (0, -1), (-1, 0) # 右下左上class Solution:def spiralOrder(self, matrix: List[List[int]]) -> List[int]:m, n = len(matrix), len(matrix[0])size = m * nans = []i, j, di = 0, -1, 0 # 从 (0, -1) 开始while len(ans) < size:dx, dy = DIRS[di]for _ in range(n): # 走 n 步(注意 n 会减少)i += dxj += dy # 先走一步ans.append(matrix[i][j]) # 再加入答案di = (di + 1) % 4 # 右转 90°n, m = m - 1, n # 减少后面的循环次数(步数)return ans
| 时间复杂度 | 空间复杂度 |
| O(mn) | O(1) |
| 其中 m 和 n 分别是矩阵的行数和列数 |
旋转图像:中等
给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。
你必须在 原地 旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。
| 示例 | 1 | 2 |
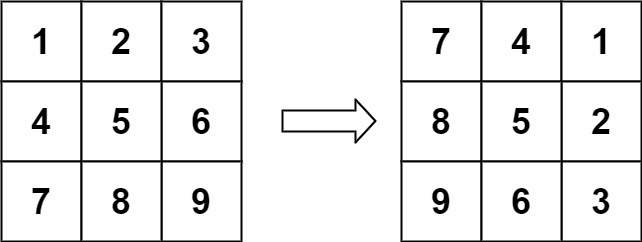
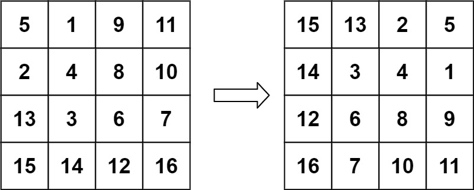
| 输入 | matrix = [[1,2,3],[4,5,6],[7,8,9]] | matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]] |
| 输出 | [[7,4,1],[8,5,2],[9,6,3]] | [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]] |
|
|
|
题意
把一个方阵(n×n 的矩阵)顺时针旋转 90o。
要求:不能创建另一个矩阵,空间复杂度必须是 O(1)。
分析
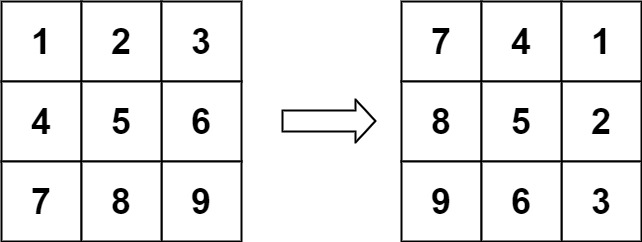
顺时针旋转90o后,位于 (i,j) 的元素去哪了?
竖着看:
- 第一列的元素去到第一行。
- 第二列的元素去到第二行。
- ……
- 第 j 列的元素去到第 j 行。
横着看:
- 第一行的元素去到最后一列。
- 第二行的元素去到倒数第二列。
- ……
- 第 i 行的元素去到第 n−1−i 列。
所以位于 i 行 j 列的元素,去到 j 行 n−1−i 列,即 (i,j)→(j,n−1−i)。
两次翻转等于一次旋转
(i,j)→(j,n−1−i) 可以通过两次翻转操作得到:

- 转置:把矩阵按照主对角线翻转,位于 (i,j) 的元素去到 (j,i)。
- 行翻转:把每一行的内部元素翻转,位于 (j,i) 的元素去到 (j,n−1−i)。
示例 1 的操作过程如下:
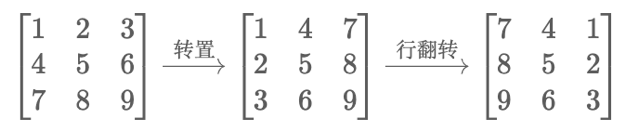
注:一般地,把一个点绕 O 旋转任意 θ 角度,可以通过两个翻转操作实现。要求这两条翻转的对称轴,交点为 O 且夹角为θ2。对于本题,每个元素需要绕矩阵中心顺时针旋转90o,这可以通过关于主对角线翻转,关于垂直中轴翻转实现。这两条对称轴的交点为矩阵中心,且夹角为45o。
实现
- 转置:把主对角线下面的元素 matrix[i][j] 和(关于主对角线)对称位置的元素 matrix[j][i] 交换。
- 行翻转:遍历每一行 row=matrix[i],把左半边的元素 row[j] 和(关于垂直中轴)对称位置的元素 row[n−1−j] 交换。或者,使用库函数翻转 row。
这两步操作都可以原地实现。
class Solution:def rotate(self, matrix: List[List[int]]) -> None:n = len(matrix)# 第一步:转置for i in range(n):for j in range(i): # 遍历对角线下方元素matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]# 第二步:行翻转for row in matrix:row.reverse()
| 时间复杂度 | 空间复杂度 |
| O(n2) | O(1) |
| 其中n 是矩阵的行数和列数 |