【备战2025数模国赛】(三)数模常见赛题类型及解决办法
在进行数学建模竞赛时,很多同学面临的第一个挑战是如何对赛题进行归类,并选择合适的模型。本篇梳理了数学建模中最常见的几类赛题,并针对每类题型提供了基本的解决思路,帮助大家快速选择合适的解题方法,高效完成模型构建。
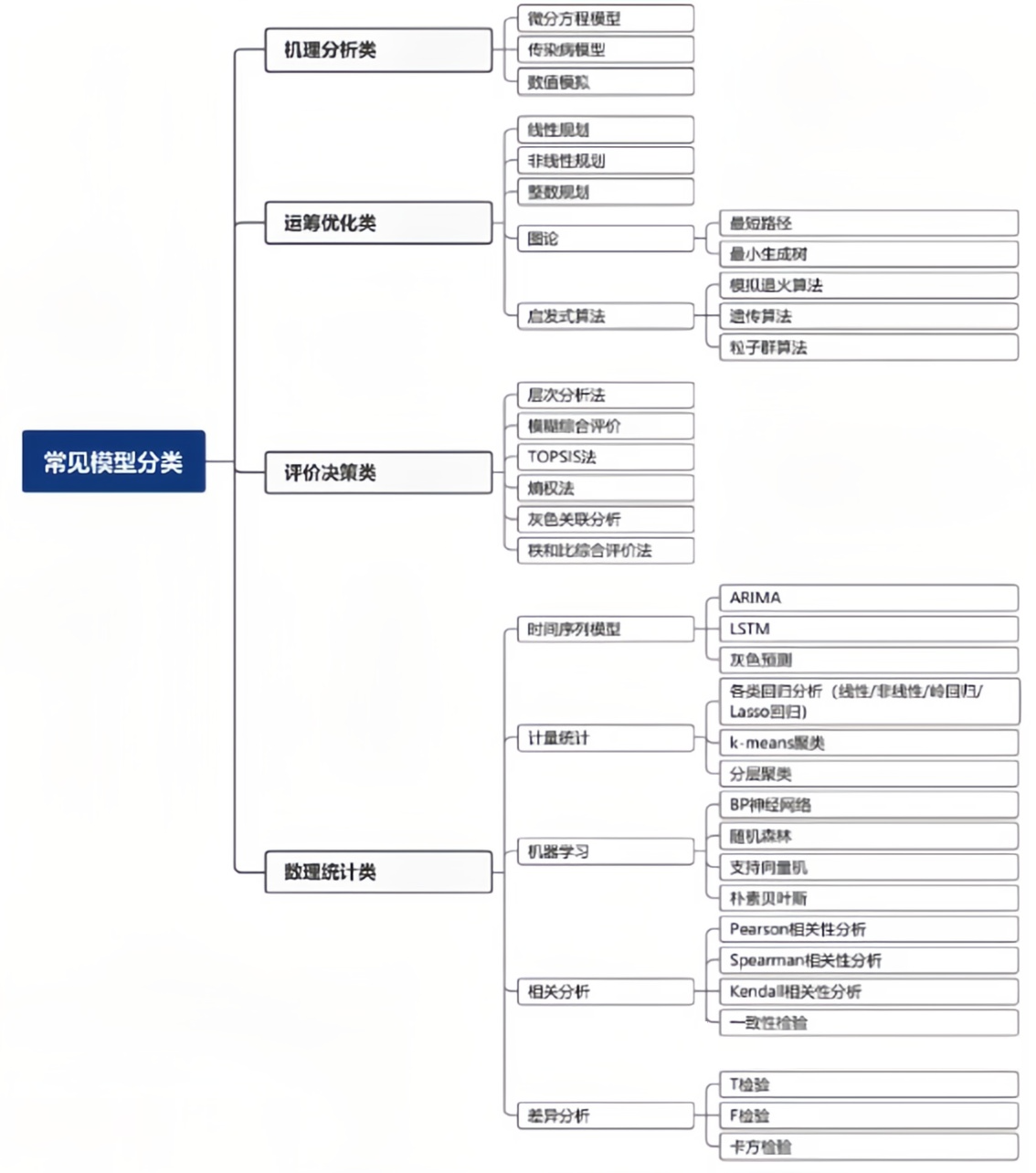
数学建模赛题类型主要分为评价类、预测类和优化类三种,其中优化类是最常见的赛题类型,几乎每年的地区赛或国赛美赛等均有出题,必须要掌握并且熟悉。机理分析类基本上建立完机理方程后仍然要转换成优化问题,数理统计类大部分都是和预测相关。
一、评价类问题
1.赛题特征与基本解题步骤
综合评价是数学建模中的一类常见的问题,在国赛和美赛中都经常出现,例如国赛05年长江水质的综合评价、2010年上海世博会影响力的定量评估问题、2014年美赛“最好大学教练”问题、2015年的“互联网+”时代的出租车资源配等,都属于综合评价类问题。综合评价问题是数学建模问题中思路相对清晰的一类题目,从每学期的综合测评、旅游景点的选择到挑选手机,评价类问题在生活中也是处处存在。
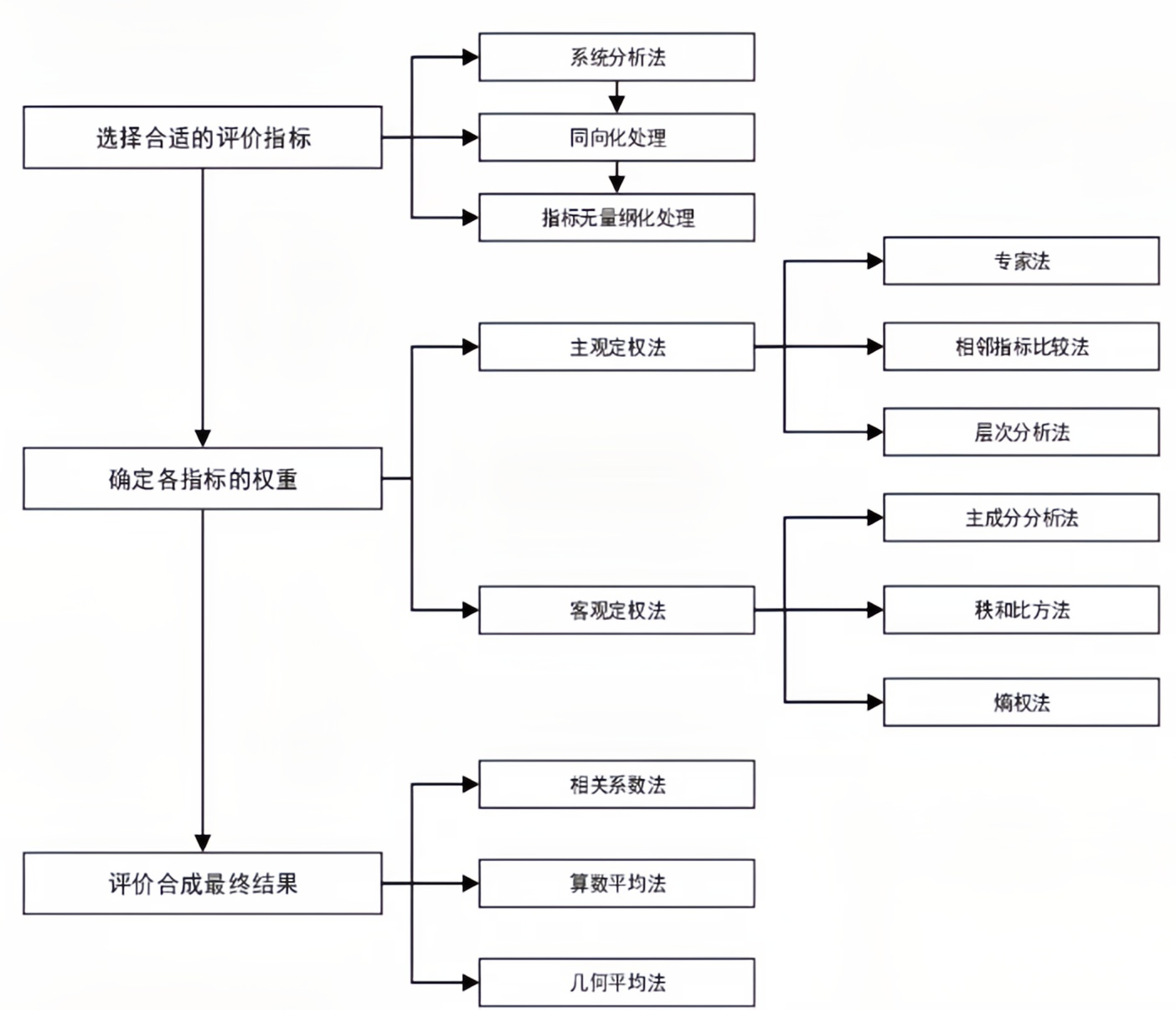
- 评价类问题一般的解题步骤为:选择合适的评价指标→确定各指标权重→评价合成最终结果
2.主客观评价问题的区别
主客观概念主要是在指标定权时来划分的。
- 主观评价:在定权时主要以判断者的主观经验为依据
- 客观评价:主要基于测量数据的基本特性来综合定权
定权带有一定的主观性,用不同方法确定的权重分配,可能不尽一致,这将导致权重分配的不确定性,最终可能导致评价结果的不确定性。因而在实际工作中,不论用哪种方法确定权重分配,都应当依赖于较为合理的专业解释。
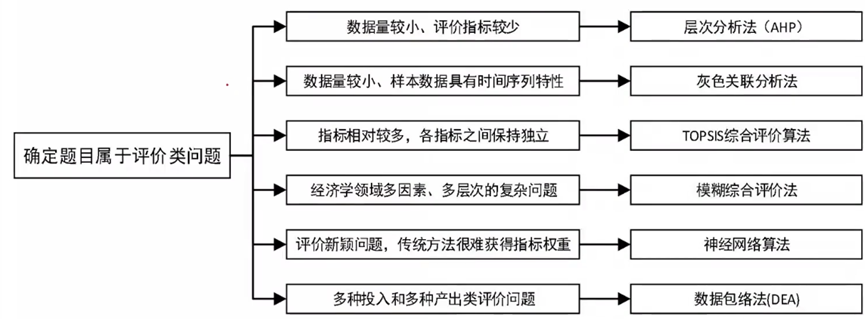
3.如何选择合适的评价方法
在评价类问题的分析中,如何选择合适的评价方法是决定评价结果好坏的关键因素,因此需要洞悉各常用评价方法的基本特性和使用条件才能顺利答题。
二、预测类问题
1.赛题特征与基本解题步骤
预测就是根据过去和现在估计未来,预测未来。统计预测属于预测方法研究范畴,即如何利用科学的统计方法对事物的未来发展进行定量推测。基于数学建模的预测方法种类繁多,从经典的单耗法、弹性系数法、统计分析法,到目前的灰色预测法、机器学习等。当在使用相应的预测方法建立预测模型时,我们需要知道主要的一些预测方法的研究特点,优缺点和适用范围。
- 预测类问题一般的解题步骤为:确定预测目的→搜索和审核资料→选择预测模型和方法→分析预测误差改进模型→给出预测结果
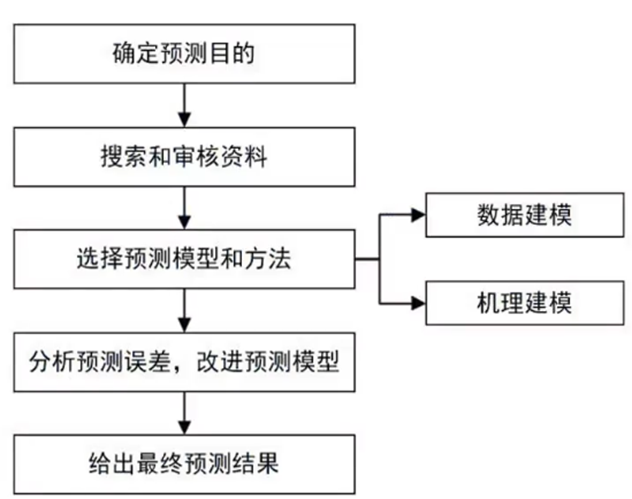
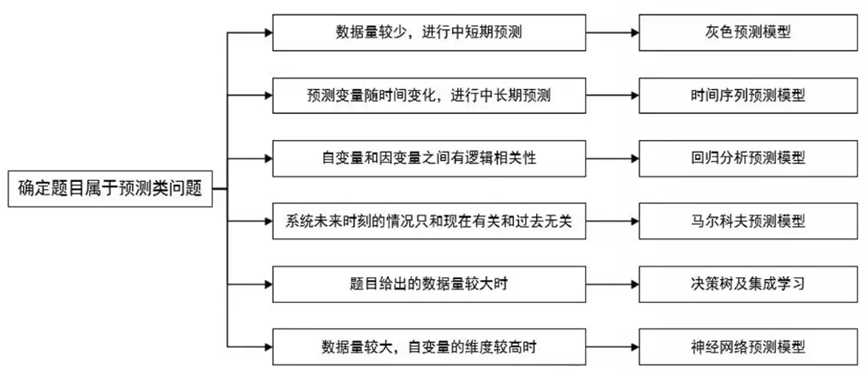
2.预测类问题分类
一类是无法用数学语言刻画其内部演化机理的问题;另一类是可以通过微分方程刻画其内部规律,称为机理建模问题,通过微分方程建模求解。
3.如何选择合适的预测方法
在预测类问题的分析中,同样受到预测条件的限制(如数据量的大小、变量之间的关系等),不同的预测方法可能会产生不同的结果,因此需要根据实际情况来选择。
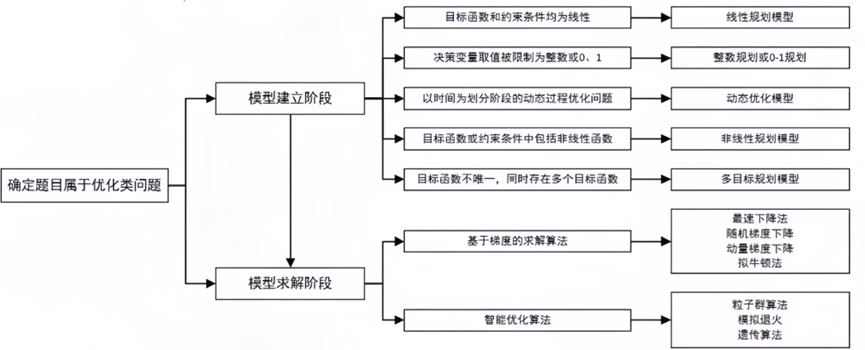
三、优化类问题
1.赛题特征与基本解题步骤
优化类问题是从所有可能方案中选择最合理的方案以达到最优目标。在各种科学问题、工程问题、生产管理、社会经济问题中,人们总是希望在有限的资源条件下,用尽可能小的代价,获得最大的收获(比如保险)。
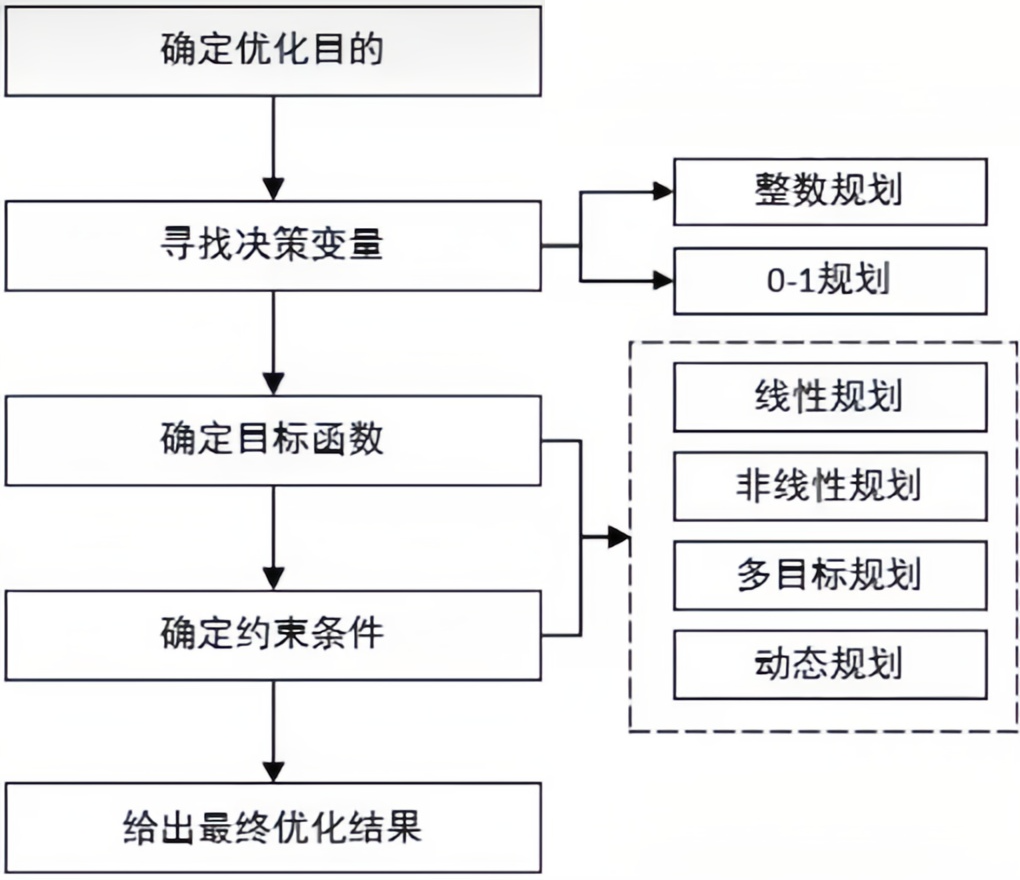
优化类问题一般的解题步骤为:
- 确定决策变量,即需要优化的变量;
- 确定目标函数,即优化的目的;
- 确定约束条件,即决策变量在达到最优状态时,受到那些客观限制。
2.部分优化类赛题的解决方案
例1:在08年国赛眼科病床的合理安排问题中——
- 目标函数:医院病床的利用率最高;
- 决策变量:服务策略,即是先到病人先住院、急诊病人先住院还是占用病床时间短的病人先住院等;
- 约束条件:可能包括病人最长等待时间限制、不同症状之间的病人不同房等。
例2:在10年国赛交巡警服务平台的设置与调度问题中——
- 决策变量:服务平台的位置坐标;
- 目标函数:交巡警车到达事发地时间最短、交巡警封锁交通要道时间最短;
- 约束条件:可能包括事故发生后交警最晚到达时间,一定区域内服务平台最低数量要求等。
3.如何选择合适的优化方法
优化类问题中常用的数学模型和求解算法,包括线性规划、非线性规划、整数规划、多目标规划等。在模型求解中,对于凸优化模型,可以采用基于梯度的求解算法;对于非凸的优化模型,可以采用智能优化算法。