Python实现点云基于法向量、曲率和ISS提取特征点
今天我们分享点云的特征点提取,这是三维数据处理中的关键步骤,它有助于识别和提取点云中具有显著几何特征的关键点。以下是点云基于法向量、曲率和ISS(Intrinsic Shape Signatures)提取特征点的方法总结:
1) 法向量夹角法(Edge-Aware)
1.1核心思想
把“表面朝向变化剧烈”当成特征。对每个点求法向量,再算它与邻域法向量的夹角 θ;θ 大即为潜在边缘或角点。1.2流程
1. 读点云 → 2. K 近邻求法向量 → 3. 计算 θ 并取平均/最大值 → 4. 设阈值挑出大 θ 点 → 5. 放大并着色 → 6. 可视化。1.3用途
边缘检测、跨视角粗配准、三维重建轮廓增强。2) 曲率法(Curvature-Saliency)
2.1核心思想
把“局部弯曲程度高”当成特征。对每个点构造协方差矩阵 C,特征值 λ₁≥λ₂≥λ₃,曲率 κ = λ₃ /(λ₁+λ₂+λ₃);κ 大即是棱角、脊或谷。2.2流程
1. 读点云 → 2. K 近邻求法向量 → 3. 算 κ → 4. 设阈值取高 κ 点 → 5. 放大着色 → 6. 可视化。2.3用途
精细三维重建、物体识别、多视角精配准。3) ISS(Intrinsic Shape Signatures)
3.1核心思想
在“形状固有”尺度上寻找跨视角稳定的显著点。结合局部协方差矩阵特征值差异与多尺度非极大值抑制,保证既显著又鲁棒。3.2流程
1. 对每个点计算邻域协方差矩阵 → 2. 特征值分解得 λ₁,λ₂,λ₃ → 3. 设定比率阈值筛显著点 → 4. 多尺度重复 → 5. NMS 去冗余 → 6. 保留 ISS 关键点。3.3用途
三维物体识别与匹配、SLAM 定位建图、机器人导航、医学影像比对。
一句话总结就是:法向量法看“朝向突变”,曲率法看“弯曲剧烈”,ISS 法看“跨尺度稳定”,三者互补,共同构成点云几何特征提取的“三驾马车”。
本次使用的数据依然是——————兔砸!
一、各种特征点提取程序
import open3d as o3d
import numpy as np
import time# ---------------- 工具函数 ----------------
def keypoints_to_spheres(keypoints, radius=1.0, color=[1, 0, 0]):mesh = o3d.geometry.TriangleMesh()for p in keypoints.points:sp = o3d.geometry.TriangleMesh.create_sphere(radius).translate(p)sp.paint_uniform_color(color)mesh += spreturn mesh# ---------------- KDTree 加速版本 ----------------
def extract_by_normal_fast(pcd, angle_th_deg=30, radius=0.1, max_nn=30):"""Open3D 自带 KDTree + 批量法向量夹角"""if not pcd.has_normals():pcd.estimate_normals(search_param=o3d.geometry.KDTreeSearchParamHybrid(radius, max_nn))# 构建 KDTree(C++ 实现)kdtree = o3d.geometry.KDTreeFlann(pcd)pts = np.asarray(pcd.points)normals = np.asarray(pcd.normals)angle_th = np.radians(angle_th_deg)mask = np.zeros(len(pts), dtype=bool)for i in range(len(pts)):[_, idx, _] = kdtree.search_radius_vector_3d(pts[i], radius)if len(idx) < 2:continuenbr_normals = normals[idx]cos_vals = np.clip(np.dot(nbr_normals, normals[i]), -1.0, 1.0)angles = np.arccos(cos_vals)if angles.mean() > angle_th:mask[i] = Truereturn pcd.select_by_index(np.where(mask)[0])def extract_by_curvature_fast(pcd, curv_th=0.1, radius=0.1, max_nn=30):"""KDTree + 批量协方差/曲率"""if not pcd.has_normals():pcd.estimate_normals(search_param=o3d.geometry.KDTreeSearchParamHybrid(radius, max_nn))kdtree = o3d.geometry.KDTreeFlann(pcd)pts = np.asarray(pcd.points)curvatures = np.zeros(len(pts))for i in range(len(pts)):[_, idx, _] = kdtree.search_radius_vector_3d(pts[i], radius)if len(idx) < 3:continuecov = np.cov(pts[idx].T)eigvals = np.linalg.eigh(cov)[0]curvatures[i] = eigvals[0] / (eigvals.sum() + 1e-12)return pcd.select_by_index(np.where(curvatures > curv_th)[0])def extract_by_iss(pcd, salient_radius=5, non_max_radius=5,gamma_21=0.5, gamma_32=0.5):tic = time.time()kpts = o3d.geometry.keypoint.compute_iss_keypoints(pcd, salient_radius, non_max_radius, gamma_21, gamma_32)toc = 1000 * (time.time() - tic)print(f"ISS {len(kpts.points)} keypoints, {toc:.1f} ms")return kpts# ---------------- 主菜单 ----------------
def main():file_path = "E:/CSDN/规则点云/bunny.pcd"pcd = o3d.io.read_point_cloud(file_path)if not pcd.has_points():print("加载失败!")returnprint(f"Loaded {len(pcd.points)} points")o3d.visualization.draw_geometries([pcd], window_name="Original",width = 768, height = 768,left = 150, top = 150)while True:choice = input("\n1) 法向量夹角 2) 曲率 3) ISS 4) 退出\n选择:").strip()if choice == "1":th = float(input("夹角阈值(°) 默认30:") or 30)r = float(input("搜索半径 默认0.005:") or 0.005)feature = extract_by_normal_fast(pcd, th, radius=r)elif choice == "2":th = float(input("曲率阈值 默认0.1:") or 0.1)r = float(input("搜索半径 默认0.005:") or 0.005)feature = extract_by_curvature_fast(pcd, th, radius=r)elif choice == "3":sr = float(input("salient_radius 默认0.005:") or 0.005)nr = float(input("non_max_radius 默认0.005:") or 0.005)feature = extract_by_iss(pcd, sr, nr)elif choice == "4":breakelse:print("无效选项")continueif len(feature.points) == 0:print("未提取到特征点!")continuepcd.paint_uniform_color([1, 0, 0])if choice == "3":spheres = keypoints_to_spheres(feature, radius=0.005)o3d.visualization.draw_geometries([pcd, spheres])else:feature.paint_uniform_color([0, 1, 0])pts = np.asarray(feature.points) * 1.02feature.points = o3d.utility.Vector3dVector(pts)o3d.visualization.draw_geometries([pcd, feature], window_name="特征点提取结果",width=768, height=768,left=150, top=150)if __name__ == "__main__":main()二、各种特征点提取结果
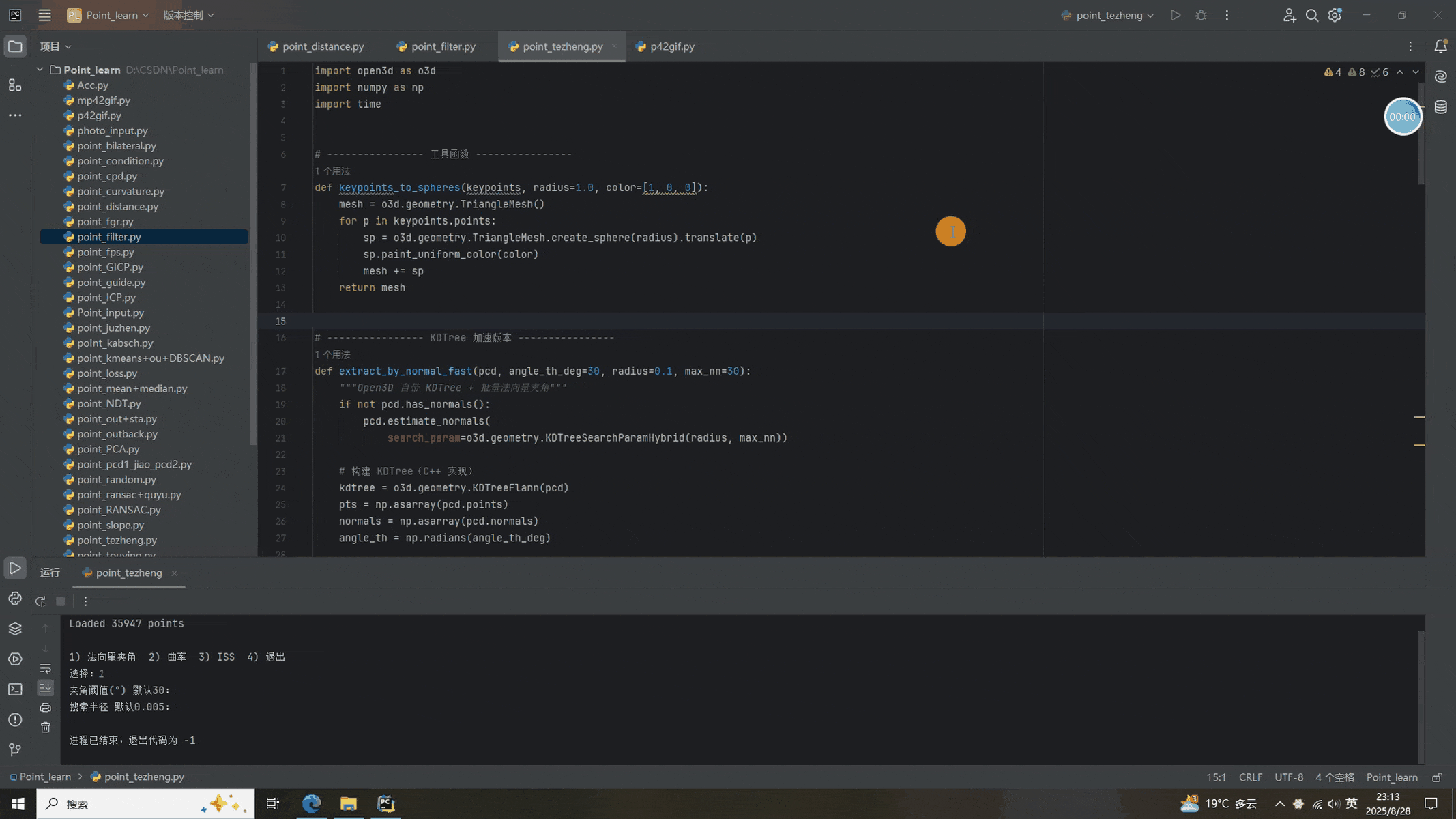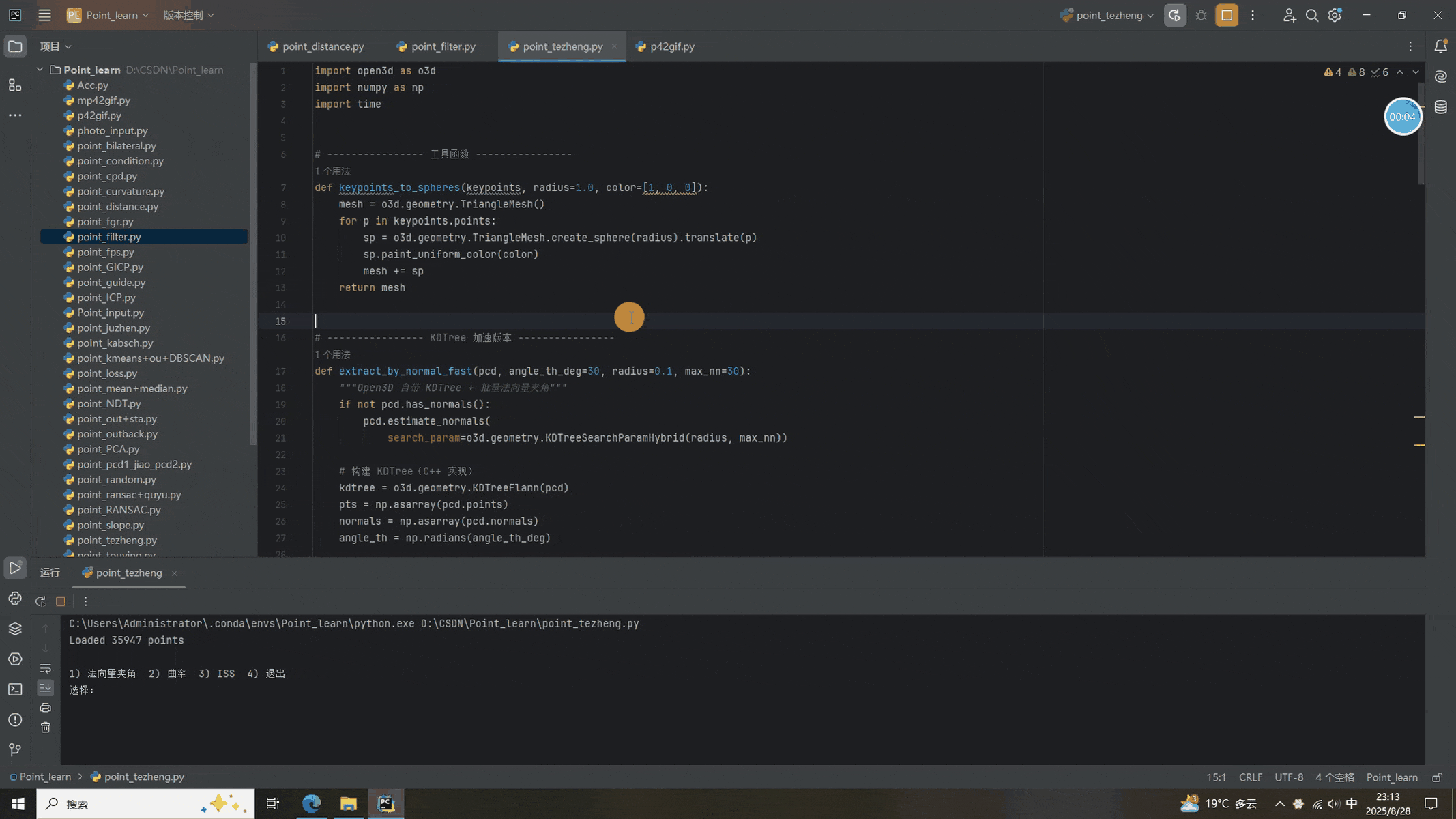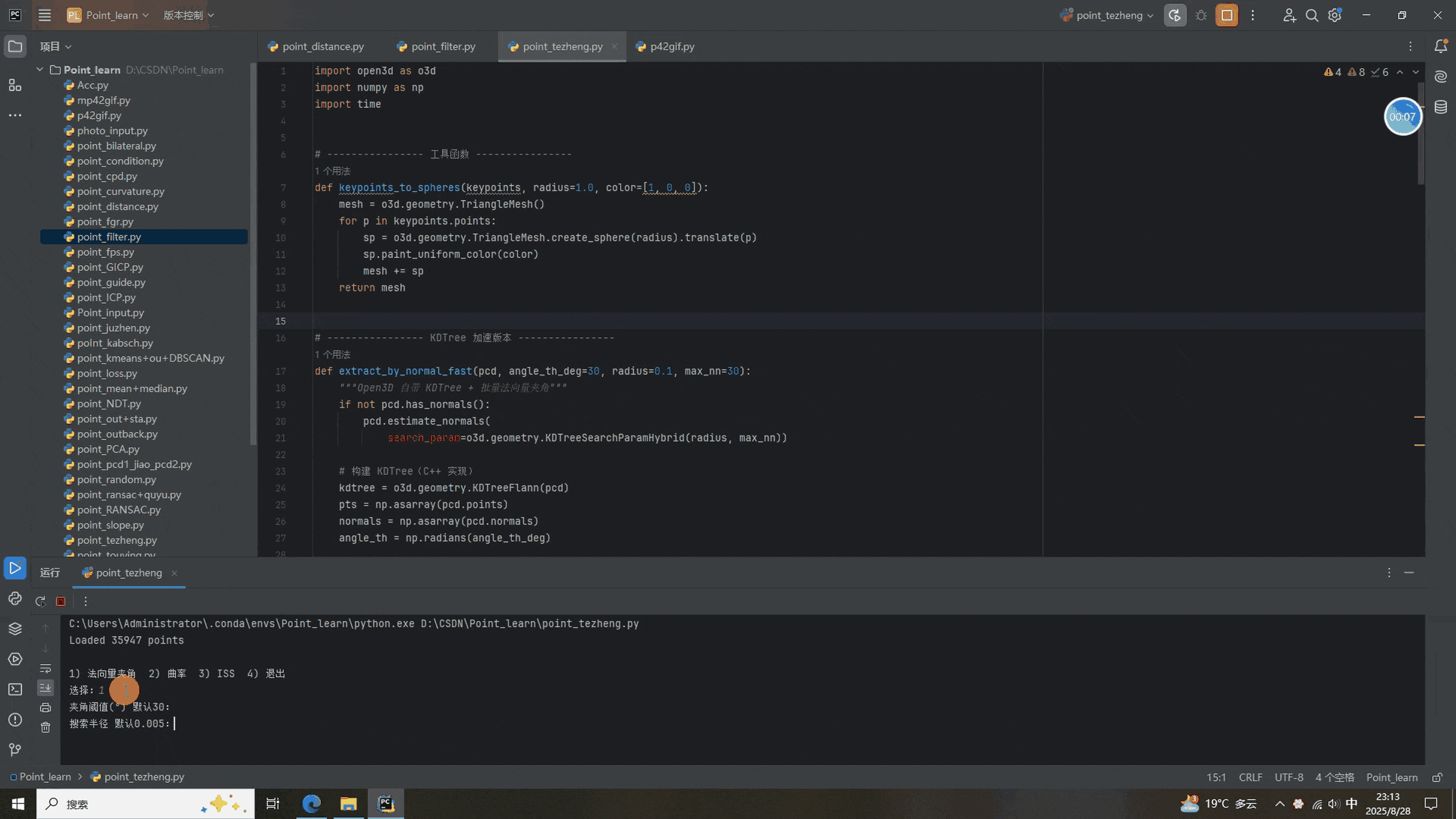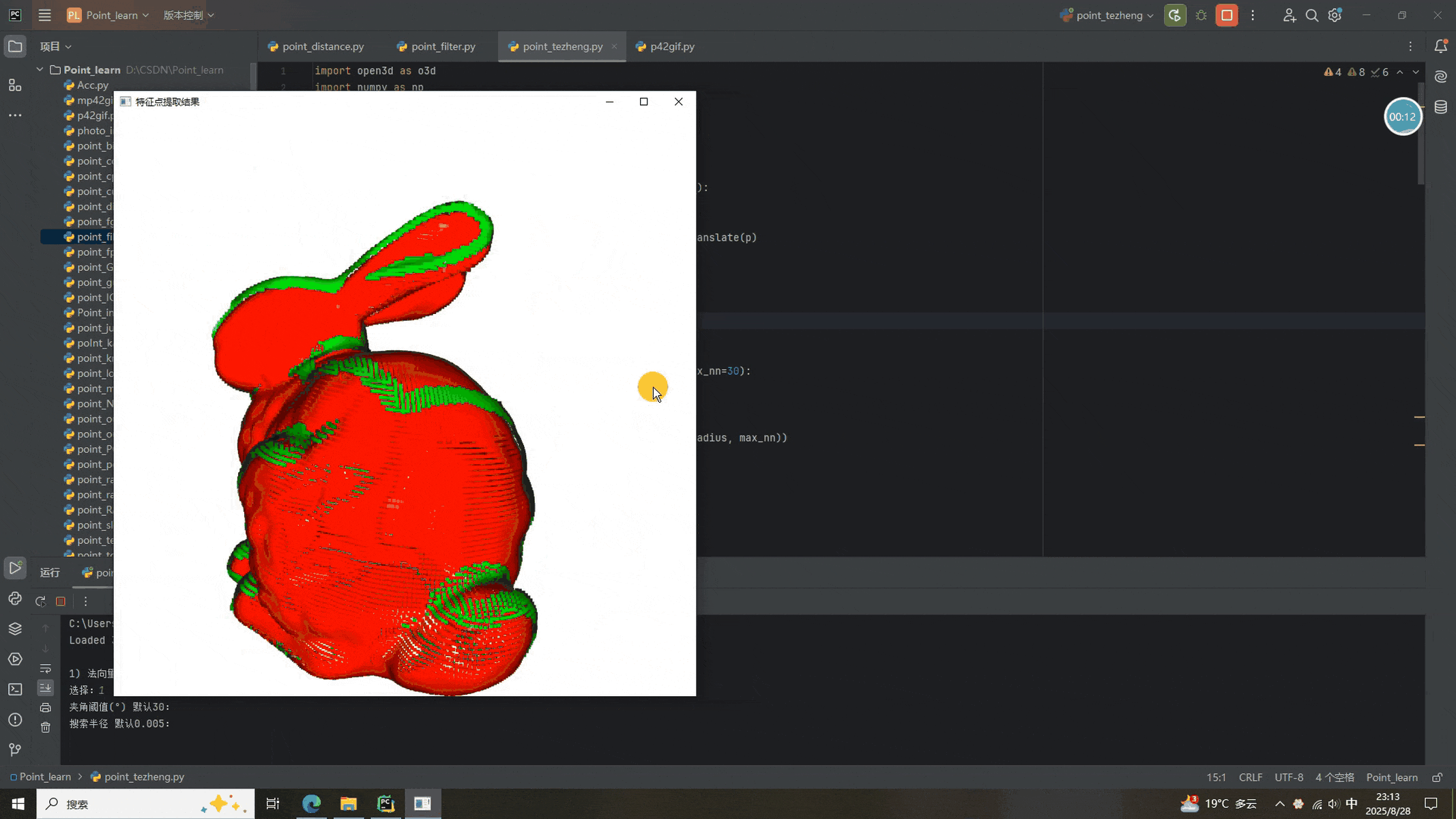
可以看到,点云的法向量特征被顺利的提取出来了(时长原因,其他两个没显示出来)。通过改变参数,特征点的提取会出现非常明显的变化,感兴趣的同学们可以试试。
就酱,下次见^-^
