泊松分布知识点讲解
一、泊松分布的起源与基本概念
1.1 历史背景与发现过程
历史起源
泊松分布得名于法国数学家西莫恩·德尼·泊松(Siméon Denis Poisson,1781-1840)。1837年,泊松在研究法庭判决中的错误率时,发现了这个重要的概率分布。有趣的是,泊松当时并没有意识到这个分布的重要性,他只是将其作为二项分布的一个近似。
现实问题的驱动
泊松分布的发现源于对以下类型问题的思考:
- 一小时内到达银行的顾客数量
- 一页书中的印刷错误数
- 一年中某地区发生地震的次数
- 单位时间内放射性物质衰变的原子数
这些问题的共同特点是:在固定的时间或空间区间内,观察某种"稀有事件"发生的次数。
1.2 泊松分布的定义与基本形式
数学定义
如果随机变量X服从参数为λ的泊松分布,记作X ~ P(λ),则其概率质量函数为:
其中:
λ > 0 是分布的唯一参数
e ≈ 2.71828是自然对数的底
k! 是k的阶乘
参数λ的物理意义
参数λ具有双重含义:
- 期望值:E(X) = λ,表示平均发生次数
- 强度参数:表示事件发生的"强度"或"频率"
例如,如果λ = 3,意味着平均每个观察期内事件发生3次。
1.3 泊松分布的适用条件
四个基本假设
泊松分布成立需要满足以下条件:
独立性:各个事件的发生相互独立
平稳性:在相同长度的时间间隔内,事件发生的概率相同
稀有性:在很短的时间间隔内,事件发生的概率很小
非聚集性:在极短的时间间隔内,最多只能发生一个事件
二、泊松分布与二项分布的关系
2.1 从二项分布到泊松分布
推导背景
泊松分布实际上是二项分布在特定条件下的极限形式。当二项分布的试验次数n很大,成功概率p很小,但乘积np保持适中时,二项分布趋近于泊松分布。
数学推导过程
设X ~ B(n, p),即X服从参数为n和p的二项分布:
1. 设定极限条件
令n → ∞(试验次数趋向无穷)
令p → 0(单次成功概率趋向零)
令np = λ(保持常数,即p = λ/n)
2. 代入并化简
3. 分别处理各项
组合数项:
当n → ∞时:
因此:
4. 处理剩余项
利用极限:
5. 最终结果:
2.2 两种分布的区别与联系
本质区别
| 特征 | 二项分布 | 泊松分布 |
|---|---|---|
| 试验性质 | 固定次数的独立试验 | 连续时间/空间中的事件计数 |
| 参数 | n(试验次数)和p(成功概率) | λ(平均发生率) |
| 取值范围 | 0, 1, 2, ..., n | 0, 1, 2, ... |
| 应用场景 | 抛硬币、产品检验 | 排队论、可靠性分析 |
实际应用中的选择
选择二项分布:
- 明确知道试验次数(如检查100个产品)
- 每次试验有明确的成功/失败结果
- 成功概率相对较大(p > 0.1)
选择泊松分布:
- 观察固定时间段内的事件次数
- 事件发生概率很小但观察次数很多
- 无法明确界定"试验次数"
经验法则
当n ≥ 20且p ≤ 0.05时,或者np ≤ 5时,可以用泊松分布近似二项分布。
三、泊松分布的数学性质与参数
3.1 基本数学性质
期望值和方差
泊松分布有一个独特的性质:期望值等于方差。
3.1.1 期望推导
( 其中用到了泰勒级数展开:
指数函数 的泰勒级数展开(也是它的定义)为:
)
3.1.2 方差推导
方差定义:随机变量 X 与其期望值之间偏差平方的期望
通过类似方法可以证明:Var(X) = λ
期望值等于方差这个性质有重要的实际意义:
- 识别标准:如果数据的均值和方差相近,可能服从泊松分布
- 模型检验:如果方差远大于均值,可能存在"过离散"现象
- 参数估计:样本均值就是λ的最佳估计
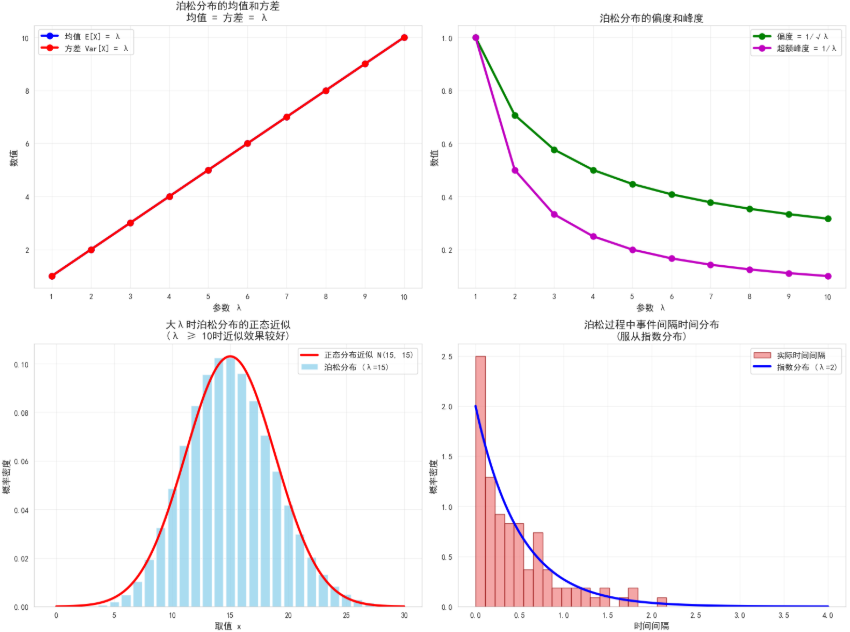
3.2 参数λ对分布形状的影响
小λ值(λ < 1)
当λ很小时:
- 分布高度右偏
- P(X = 0)是最大概率
- 大部分概率集中在0和1上
中等λ值(1 ≤ λ ≤ 10)
- 分布逐渐对称化
- 最可能值接近λ
- 分布开始呈现钟形
大λ值(λ > 10)
- 分布近似正态分布
- 可以用正态分布进行近似
- 标准差为√λ