day22 回溯算法part01
理论基础
递推本质上也是暴力求解
回溯模版框架
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) { // for循环横向处理节点;backtracking(路径,选择列表); // 递归纵向 // 递归,回溯,撤销处理结果}
}
什么样的场景时候递推
- 需要for循环的个数是不定的,可能越来越多,导致暴力写法都没法写
组合
第77题. 组合
力扣题目链接(opens new window)
给定两个整数 n 和 k,返回 1 … n 中所有可能的 k 个数的组合。
示例: 输入: n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]
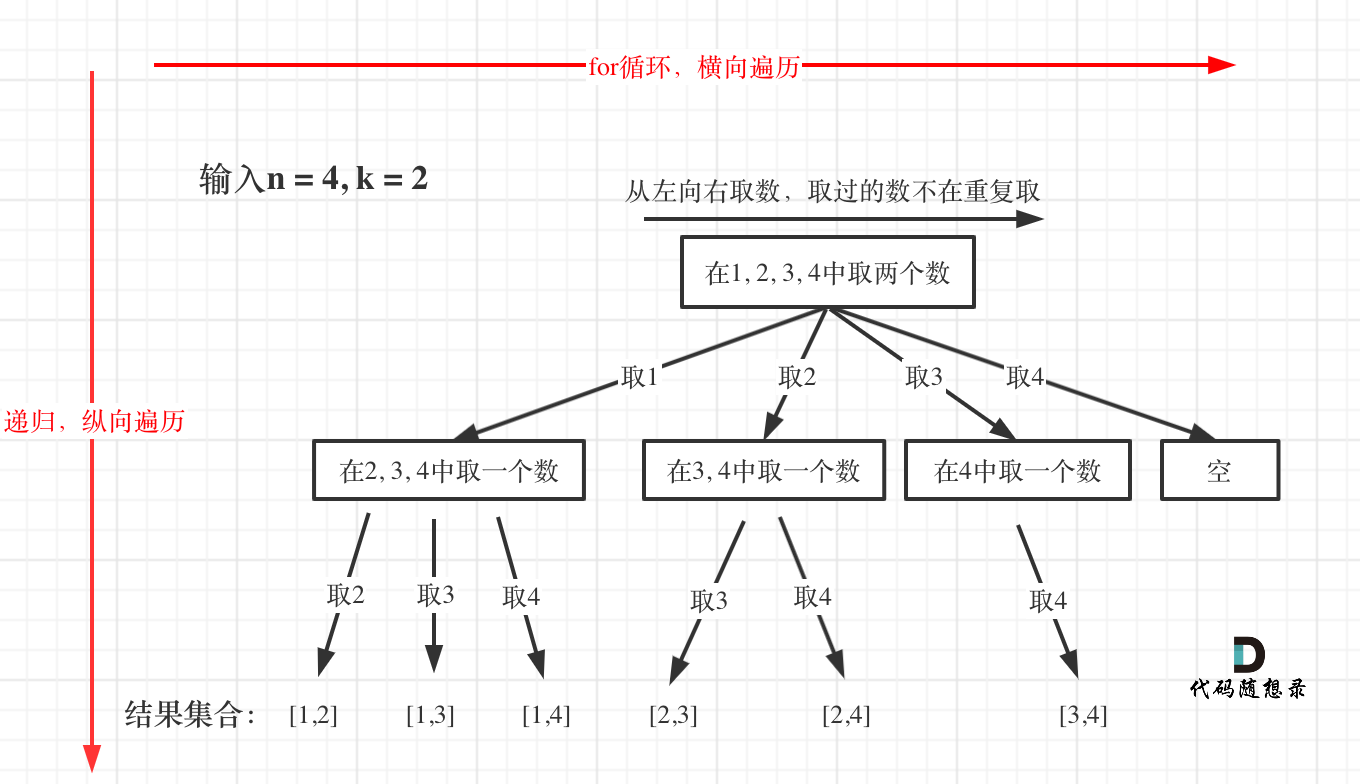
class Solution {
public:vector<vector<int>> result;vector<int> path; // 看起来像路径void backtracking(int n, int k, int startIndex){if (path.size() == k){result.push_back(path);return;}// 剪枝操作for (int i = startIndex; i <= n - (k - path.size()) + 1; i++){ // 保证后面的还够k个path.push_back(i);backtracking(n, k, i + 1);path.pop_back();}}vector<vector<int>> combine(int n, int k) {backtracking(n, k, 1);return result;}
};
组合总和III
216.组合总和III
力扣题目链接(opens new window)
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
说明:
- 所有数字都是正整数。
- 解集不能包含重复的组合。
示例 1: 输入: k = 3, n = 7 输出: [[1,2,4]]
示例 2: 输入: k = 3, n = 9 输出: [[1,2,6], [1,3,5], [2,3,4]]
class Solution {
public:vector<vector<int>> result;vector<int> path;int sum;void backtracking(int targetSum, int k, int startIndex){// n=9固定if (targetSum < 0) return; // 剪枝操作if (path.size() == k && targetSum == 0){ // 返回条件result.push_back(path);return;}for (int i = startIndex; i <= 9 - (k - path.size()) + 1; i++){path.push_back(i);targetSum -= i;backtracking(targetSum, k, i+1);path.pop_back();targetSum += i;}} vector<vector<int>> combinationSum3(int k, int n) {backtracking(n, k, 1);return result;}
};
电话号码的字母组合
17.电话号码的字母组合
力扣题目链接(opens new window)
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母
class Solution {
public:const string letterMap[10] = {"", // 0"", // 1"abc", // 2"def", // 3"ghi", // 4"jkl", // 5"mno", // 6"pqrs", // 7"tuv", // 8"wxyz", // 9};vector<string> result;string s;void backtracking(const string & digits, int index){ // index是指每个数字比如"23"中的"2"和"3"if (index == digits.size()){result.push_back(s);return;}int digit = digits[index] - '0'; // int(digits[index]) 会把字符转换成 ASCII 码值string letters = letterMap[digit];for (int i = 0; i < letters.size(); i++){ // 每一个数字代表的是不同集合s.push_back(letters[i]);backtracking(digits, index+1);s.pop_back();} }
