【数据结构】树和二叉树——树和森林

树和二叉树

树和森林

树的存储结构

双亲表示法

双亲表示法是一种用数组来存储树的结构方法。它的核心思想是：在数组中为每个结点记录其双亲结点所在的下标。

• 存储结构：
  • 使用一个数组或结构体数组来存储所有结点。
  • 每个结点包含两个字段：数据域（存储结点的值）和双亲域（存储双亲结点的数组下标）。
  • 根结点的双亲域通常用一个特殊值（例如 -1）来表示。
• 优点：
  • 查找双亲结点非常高效。给定任意一个结点，可以立即通过其双亲域找到其父结点，时间复杂度为 O(1)。
• 缺点：
  • 查找孩子结点非常麻烦。需要遍历整个数组，找到所有双亲域等于当前结点下标的结点。这个操作的时间复杂度为 O(n)，其中 n 是结点的总数。

对于一个有 N 个节点的树，用双亲表示法存储时，这个数组的大小应该是 N

因为需要为树中的每一个结点都分配一个位置，包括根结点。虽然根结点没有双亲，但它仍然是树的一部分，需要占用一个数组位置。

所以，一个大小为 N 的数组，下标从 0 到 N-1，刚好可以存储这 N 个结点，并记录它们各自的双亲位置。

假设有棵树长这样：

       A (0)/ \B(1)  C(2)/ \   /D(3) E(4) F(5)

括号里的数字是结点的数组下标。用双亲表示法来记录这棵树：

结点	数据	双亲位置
A	A	-1
B	B	0
C	C	0
D	D	1
E	E	1
F	F	2

代码示例

#include <stdio.h>#define MAX_TREE_SIZE 100 // 定义树的最大结点数// 定义双亲表示法中的结点结构
typedef struct {char data;          // 结点数据域int parent;         // 双亲结点在数组中的下标
} PTNode;// 定义树的结构
typedef struct {PTNode nodes[MAX_TREE_SIZE]; // 结点数组int num_nodes;               // 结点总数int root;                    // 根结点在数组中的下标
} PTree;int main() {PTree T;// 假设有一棵树，如之前举例的 A, B, C... F// 我们可以手动初始化这个数组T.num_nodes = 6;T.root = 0; // 根结点A的下标为0// 初始化所有结点的数据和双亲位置T.nodes[0].data = 'A';T.nodes[0].parent = -1; // 根结点A没有双亲T.nodes[1].data = 'B';T.nodes[1].parent = 0;  // B的双亲是AT.nodes[2].data = 'C';T.nodes[2].parent = 0;  // C的双亲是AT.nodes[3].data = 'D';T.nodes[3].parent = 1;  // D的双亲是BT.nodes[4].data = 'E';T.nodes[4].parent = 1;  // E的双亲是BT.nodes[5].data = 'F';T.nodes[5].parent = 2;  // F的双亲是C// 示例：查找结点F的双亲int index_of_F = 5;int parent_of_F_index = T.nodes[index_of_F].parent;printf("结点F的双亲是：%c\n", T.nodes[parent_of_F_index].data);// 示例：查找结点A的孩子们（需要遍历）printf("结点A的孩子们是：");for (int i = 0; i < T.num_nodes; i++) {if (T.nodes[i].parent == T.root) { // 如果某个结点的双亲是根结点printf("%c ", T.nodes[i].data);}}printf("\n");return 0;
}

输出结果为：

结点F的双亲是：C
结点A的孩子们是：B C

孩子表示法

与双亲表示法相反，孩子表示法着重记录每个结点的孩子结点。由于每个结点可以有多个孩子，我们不能像双亲表示法那样用一个简单的数组下标来表示。因此，孩子表示法通常采用**“顺序+链式”**的存储方式，来兼顾效率和灵活性。

具体来说，这种方法会用到两个部分：

1. 头结点数组（Parent Array）：一个数组，用于存储树中的所有结点。每个数组元素记录一个结点的数据。
2. 孩子链表（Child List）：对于每个结点，用一个单链表来连接它的所有孩子结点。

每个结点在头结点数组中都有一个位置，比如 nodes[i]。而这个结点 i 的所有孩子，则用一个链表串起来。nodes[i] 中会有一个指针，指向这个链表的第一个孩子结点。

对于一个有 N 个结点的树，用孩子表示法存储时，头结点数组的大小应该是 N。

孩子表示法的优点和缺点是什么呢？

• 优点：
  • 查找某个结点的孩子非常方便，直接通过链表遍历即可。
  • 结点可以有任意数量的孩子，动态增删孩子结点也很灵活。
• 缺点：
  • 查找双亲结点很麻烦。为了找到某个结点的双亲，你需要遍历整个头结点数组和它下面的所有孩子链表，看哪个链表里包含了这个结点。

代码示例

#include <stdio.h>
#include <stdlib.h>#define MAX_TREE_SIZE 100 // 定义树的最大结点数// 孩子链表的结点
typedef struct ChildNode {int child_index;            // 孩子结点在头结点数组中的下标struct ChildNode* next;     // 指向下一个兄弟结点
} ChildNode;// 头结点数组的结点
typedef struct {char data;                  // 结点数据ChildNode* first_child;     // 指向孩子链表的头指针
} TNode;// 树的结构
typedef struct {TNode nodes[MAX_TREE_SIZE]; // 头结点数组int num_nodes;              // 结点总数int root;                   // 根结点下标
} CTree;// 辅助函数：向指定结点添加一个孩子
void addChild(CTree* T, int parent_index, int child_index) {ChildNode* newNode = (ChildNode*)malloc(sizeof(ChildNode));newNode->child_index = child_index;newNode->next = NULL;if (T->nodes[parent_index].first_child == NULL) {T->nodes[parent_index].first_child = newNode;} else {ChildNode* p = T->nodes[parent_index].first_child;while (p->next != NULL) {p = p->next;}p->next = newNode;}
}int main() {CTree T;T.num_nodes = 6;T.root = 0;// 初始化结点数据T.nodes[0].data = 'A';T.nodes[1].data = 'B';T.nodes[2].data = 'C';T.nodes[3].data = 'D';T.nodes[4].data = 'E';T.nodes[5].data = 'F';// 建立孩子关系T.nodes[0].first_child = NULL;T.nodes[1].first_child = NULL;T.nodes[2].first_child = NULL;T.nodes[3].first_child = NULL;T.nodes[4].first_child = NULL;T.nodes[5].first_child = NULL;addChild(&T, 0, 1); // A的孩子是BaddChild(&T, 0, 2); // A的孩子是CaddChild(&T, 1, 3); // B的孩子是DaddChild(&T, 1, 4); // B的孩子是EaddChild(&T, 2, 5); // C的孩子是F// 示例：查找结点A的所有孩子printf("结点A的孩子们是：");ChildNode* p = T.nodes[0].first_child;while (p != NULL) {printf("%c ", T.nodes[p->child_index].data);p = p->next;}printf("\n");return 0;
}

孩子表示法 vs 双亲表示法：空间效率

• 双亲表示法：每个结点只需存储一个指向双亲的指针。这个指针通常是一个整数，占用的空间很小。因此，整个树的存储空间相对固定且节省。

• 孩子表示法：每个结点需要存储一个指向孩子链表的指针，而这个链表中的每个结点又需要额外分配空间来存储孩子的下标和下一个兄弟的指针。当树中分支（即孩子的数量）很多时，孩子表示法会比双亲表示法占用更多的空间。

简单来说，双亲表示法用空间换取了查找孩子的时间，而孩子表示法用空间换取了查找双亲的时间。

孩子兄弟表示法

这种方法的核心思想是：用二叉链表来存储一棵普通的树。

在孩子兄弟表示法中，每个结点包含三个域：

1. 数据域：存储结点本身的值。
2. 第一个孩子指针：指向该结点的第一个孩子。
3. 右兄弟指针：指向该结点的下一个右兄弟。

这个结构是不是看起来很熟悉？它其实就是一个二叉链表的结点结构！

• 第一个孩子指针 对应于二叉树的左孩子指针。
• 右兄弟指针 对应于二叉树的右孩子指针。

用这种方式，一棵普通的树就被“转换”成了一棵二叉树。

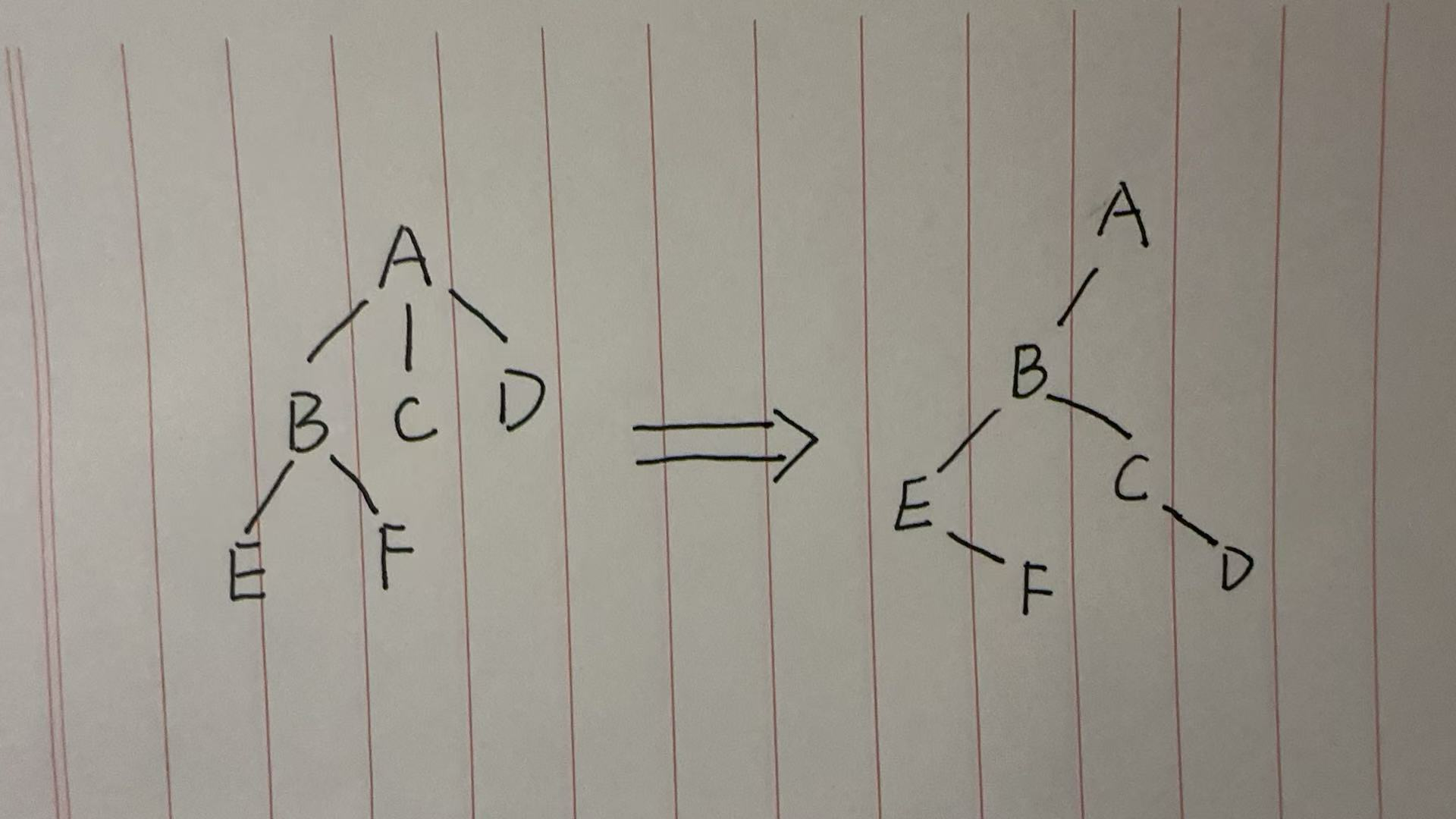
用孩子兄弟表示法，我们可以把它转换成一棵二叉树：

• 结点 A 的第一个孩子是 B，它的右兄弟是空的。
• 结点 B 的第一个孩子是 E，它的右兄弟是 C。
• 结点 C 的第一个孩子是空的，它的右兄弟是 D。
• 结点 D 的第一个孩子是空的，它的右兄弟是空的。
• 结点 E 的第一个孩子是空的，它的右兄弟是 F。
• 结点 F 的第一个孩子是空的，它的右兄弟是空的。

这就是孩子兄弟表示法的精髓：

• 垂直方向的连接（树的层级）被转换成了左孩子连接。
• 水平方向的连接（兄弟结点）被转换成了右兄弟连接。

通过这种巧妙的转换，一棵普通的多叉树，就可以用我们熟悉的二叉树结构来表示和存储。

实际上就是树到二叉树的转换。这是一种非常有用的技术，因为：

1. 实现简单：许多树的操作，比如遍历，可以直接套用成熟的二叉树算法。
2. 节约空间：避免了为每个结点动态分配不定数量的指针。

下面是孩子兄弟表示法的代码示例。它的结点结构和二叉链表完全一样，只是指针的语义不同。

#include <stdio.h>
#include <stdlib.h>// 树结点结构（其实就是二叉树结点）
typedef struct CSNode {char data;                 // 结点数据域struct CSNode* first_child;  // 指向第一个孩子struct CSNode* next_sibling; // 指向下一个兄弟
} CSNode, *CSTree;// 辅助函数：创建新结点
CSNode* createNode(char data) {CSNode* newNode = (CSNode*)malloc(sizeof(CSNode));newNode->data = data;newNode->first_child = NULL;newNode->next_sibling = NULL;return newNode;
}int main() {// 假设有棵树：A->B,C,D; B->E,F// 手动构建这棵树的孩子兄弟表示CSNode* A = createNode('A');CSNode* B = createNode('B');CSNode* C = createNode('C');CSNode* D = createNode('D');CSNode* E = createNode('E');CSNode* F = createNode('F');// 建立孩子和兄弟关系A->first_child = B;         // A的第一个孩子是BB->next_sibling = C;        // B的右兄弟是CC->next_sibling = D;        // C的右兄弟是DB->first_child = E;         // B的第一个孩子是EE->next_sibling = F;        // E的右兄弟是F// C,D,E,F没有孩子，它们的first_child都是NULL// D,F没有右兄弟，它们的next_sibling都是NULL// 示例：查找结点A的所有孩子printf("结点A的孩子们是：");CSNode* p = A->first_child;while (p != NULL) {printf("%c ", p->data);p = p->next_sibling;}printf("\n");return 0;
}

输出结果为：

结点A的孩子们是：B C D 

孩子兄弟表示法的优缺点：

• 查找孩子非常方便，直接通过左孩子指针找到第一个孩子，再通过右兄弟指针遍历所有兄弟。
• 查找双亲相对麻烦，需要从根结点开始遍历才能找到。如果在结点中额外增加一个双亲指针，就可以解决这个问题，但会增加空间消耗。

孩子兄弟表示法是最适合快速查找所有孩子的方法

• 双亲表示法：需要遍历整个数组，找到所有双亲指针指向当前节点的节点，时间复杂度是 O(n)，效率很低。

• 孩子表示法：需要遍历孩子链表。虽然比双亲表示法好，但还是需要顺着链表一个个找，效率取决于孩子的数量。

• 孩子兄弟表示法：只需要一个指针操作，就能找到第一个孩子（左孩子），然后通过右兄弟指针，就能像遍历链表一样，高效地访问所有兄弟节点。这个过程非常直接。

森林与二叉树的转换

就像单棵树可以转换为二叉树一样，一个森林也可以通过孩子兄弟表示法转换成一棵唯一的二叉树。

转换规则是：

1. 把森林中第一棵树的根作为转换后二叉树的根。
2. 把第一棵树的子树，用孩子兄弟表示法连接起来，作为转换后二叉树的左子树。
3. 把森林中除了第一棵树之外的其他树，用孩子兄弟表示法连接起来，作为转换后二叉树的右子树。

假设有一个森林，由两棵树组成：

树1:

       A/ \B   C

树2:

       D/ \E   F

现在，用上述规则将这个森林转换成一棵二叉树：

1. 森林中的第一棵树的根是 A，所以 A 成为新二叉树的根。
2. 树1 的子树是 B 和 C。我们把 B 作为 A 的左孩子，把 C 作为 B 的右兄弟。
3. 森林中的第二棵树是树2，其根是 D。我们把 D 作为 A 的右兄弟。

最终，转换后的二叉树是这样的：

        A/   \B     D\   / C E   \F

树和森林的遍历

树的先根遍历

树的先根遍历，顾名思义，是按照“先访问根节点，再依次访问它的子树”的顺序来进行的。

由于树的子树之间没有严格的左右之分，我们通常约定一个访问顺序（比如从左到右）。

以这棵树为例：

       A/|\B C D/ \E   F

它的先根遍历过程是：

1. 访问根节点A。
2. 访问A的第一个子树，其根节点是B。
   • 访问B。
   • 访问B的第一个子树，其根节点是E。
     • 访问E。
   • 访问B的第二个子树，其根节点是F。
     • 访问F。
3. 访问A的第二个子树，其根节点是C。
   • 访问C。
4. 访问A的第三个子树，其根节点是D。
   • 访问D。

所以，这棵树的先根遍历结果是：A B E F C D。

代码示例：

#include <stdio.h>
#include <stdlib.h>// 树结点结构（即二叉树结点）
typedef struct CSNode {char data;struct CSNode* first_child;  // 指向第一个孩子（对应二叉树的左孩子）struct CSNode* next_sibling; // 指向下一个兄弟（对应二叉树的右孩子）
} CSNode, *CSTree;// 辅助函数：创建新结点
CSNode* createNode(char data) {CSNode* newNode = (CSNode*)malloc(sizeof(CSNode));newNode->data = data;newNode->first_child = NULL;newNode->next_sibling = NULL;return newNode;
}// 树的先根遍历（本质上是二叉树的先序遍历）
void PreOrderTraverse(CSTree T) {if (T) {// 1. 访问根结点printf("%c ", T->data);// 2. 递归遍历它的第一个孩子（左子树）PreOrderTraverse(T->first_child);// 3. 递归遍历它的右兄弟（右子树）PreOrderTraverse(T->next_sibling);}
}int main() {// 假设有棵树：A->B,C,D; B->E,F// 用孩子兄弟表示法构建这棵树CSNode* A = createNode('A');CSNode* B = createNode('B');CSNode* C = createNode('C');CSNode* D = createNode('D');CSNode* E = createNode('E');CSNode* F = createNode('F');// 建立孩子和兄弟关系A->first_child = B;         // A的第一个孩子是BB->next_sibling = C;        // B的右兄弟是CC->next_sibling = D;        // C的右兄弟是DB->first_child = E;         // B的第一个孩子是EE->next_sibling = F;        // E的右兄弟是Fprintf("树的先根遍历序列为：");PreOrderTraverse(A);printf("\n");return 0;
}

这段代码的核心是 PreOrderTraverse 函数:

• T->data 对应于先序遍历中的“访问根结点”。
• T->first_child 对应于先序遍历中的“遍历左子树”。
• T->next_sibling 对应于先序遍历中的“遍历右子树”。

输出结果为：

树的先根遍历序列为：A B E F C D 

树的先根遍历与二叉树的先序遍历

一棵普通树的先根遍历序列，与该树转换成二叉树后的先序遍历序列是完全一样的。

将上述树转换为孩子兄弟表示法的二叉树：

       A/B --- C --- D/E --- F

二叉树的先序遍历顺序是：根 -> 左子树 -> 右子树。

1. 访问根结点 A。
2. 进入左子树：A 的左孩子是 B，所以进入以 B 为根的子树。
   • 访问根结点 B。
   • 进入左子树：B 的左孩子是 E，所以进入以 E 为根的子树。
     • 访问根结点 E。
     • 进入左子树：E 没有左孩子，所以跳过。
     • 进入右子树：E 的右兄弟是 F。
       • 访问根结点 F。
       • F 没有左孩子和右兄弟，所以回到上一层。
     • 回到 E 结点，它的左右子树都遍历完了，所以回到 B 结点。
   • 进入右子树：B 的右兄弟是 C。
     • 访问根结点 C。
     • C 没有左孩子，进入右子树。C 的右兄弟是 D。
       • 访问根结点 D。
       • D 没有左孩子和右兄弟，回到上一层。
     • 回到 C 结点，它的左右子树都遍历完了，所以回到 B 结点。
   • 回到 B 结点，它的左右子树都遍历完了，所以回到 A 结点。
3. 进入右子树：A 没有右兄弟，遍历结束。

最终得到的先序遍历序列是：A B E F C D。

树的后根遍历

树的后根遍历，也叫后序遍历，顾名思义，是按照“先访问所有子树，最后访问根节点”的顺序来进行的。

与先根遍历类似，它也与孩子兄弟表示法的二叉树有直接联系：

一棵普通树的后根遍历序列，与该树转换成二叉树后的后序遍历序列是完全一样的。

       A/|\B C D/ \E   F

再来看一下这棵树的正确转换：

       A/B --- C --- D/E --- F

后根遍历的步骤是：

1. 从左到右依次访问所有子树。
2. 最后访问根节点。

来一步步分析：

1. 访问 A 的所有子树：以 B、C、D 为根的子树。
   • 先访问 B 的子树：以 E、F 为根。
     • 访问 E 的子树：无。
     • 访问 F 的子树：无。
     • 最后访问 B。
   • 再访问 C 的子树：无。
   • 再访问 D 的子树：无。
2. 最后访问根节点 A。

所以，这棵树的后根遍历序列是：E F B C D A。

代码示例

#include <stdio.h>
#include <stdlib.h>// 树结点结构（即二叉树结点）
typedef struct CSNode {char data;struct CSNode* first_child;  // 指向第一个孩子（对应二叉树的左孩子）struct CSNode* next_sibling; // 指向下一个兄弟（对应二叉树的右孩子）
} CSNode, *CSTree;// 辅助函数：创建新结点
CSNode* createNode(char data) {CSNode* newNode = (CSNode*)malloc(sizeof(CSNode));newNode->data = data;newNode->first_child = NULL;newNode->next_sibling = NULL;return newNode;
}// 树的后根遍历（本质是二叉树的后序遍历）
void PostOrderTraverse(CSTree T) {if (T) {// 1. 递归遍历第一个孩子（左子树）PostOrderTraverse(T->first_child);// 2. 递归遍历右兄弟（右子树）PostOrderTraverse(T->next_sibling);// 3. 最后访问根结点printf("%c ", T->data);}
}int main() {// 假设有棵树：A->B,C,D; B->E,F// 用孩子兄弟表示法构建这棵树CSNode* A = createNode('A');CSNode* B = createNode('B');CSNode* C = createNode('C');CSNode* D = createNode('D');CSNode* E = createNode('E');CSNode* F = createNode('F');// 建立孩子和兄弟关系A->first_child = B;B->next_sibling = C;C->next_sibling = D;B->first_child = E;E->next_sibling = F;printf("树的后根遍历序列为：");PostOrderTraverse(A);printf("\n");return 0;
}

运行结果：

树的后根遍历序列为：E F B C D A

树的层次遍历

树的层次遍历，顾名思义，是按照树的层次顺序，从上到下、从左到右依次访问树中的每一个结点。

这个过程就像是你从树的顶端（根结点）开始，一层一层地往下走，把每层遇到的结点都收集起来。

我们再用这棵树来举例：

       A/|\B C D/ \E   F

它的层次遍历过程是：

1. 第一层：只有根结点 A。
2. 第二层：从左到右依次是 B、C、D。
3. 第三层：从左到右依次是 E、F。

所以，这棵树的层次遍历结果是：A B C D E F。

如何实现层次遍历？

与先根、后根遍历不同，层次遍历无法使用简单的递归来实现。这是因为递归的本质是“先深入子树”，而层次遍历要求“先访问同一层的所有结点”。

为了实现层次遍历，我们通常使用队列（Queue）这种数据结构。队列的特点是先进先出（FIFO）。

算法步骤：

1. 创建一个空队列，并将根结点放入队列中。
2. 只要队列不为空，就重复以下操作：
   • 将队列的队首结点出队。
   • 访问该结点。
   • 将该结点的所有孩子结点（如果有）从左到右依次入队。

通过这个过程，队列中总是按序存放着下一层需要访问的结点，从而保证了层次遍历的顺序。

代码示例

#include <stdio.h>
#include <stdlib.h>// 树结点结构（使用孩子兄弟表示法）
typedef struct CSNode {char data;struct CSNode* first_child;struct CSNode* next_sibling;
} CSNode, *CSTree;// 队列结点
typedef struct QNode {CSTree data;struct QNode* next;
} QNode;// 队列结构
typedef struct {QNode* front;QNode* rear;
} Queue;// 辅助函数：初始化队列
void initQueue(Queue* Q) {Q->front = Q->rear = NULL;
}// 辅助函数：入队
void enqueue(Queue* Q, CSTree T) {QNode* p = (QNode*)malloc(sizeof(QNode));p->data = T;p->next = NULL;if (Q->rear == NULL) {Q->front = Q->rear = p;} else {Q->rear->next = p;Q->rear = p;}
}// 辅助函数：出队
CSTree dequeue(Queue* Q) {if (Q->front == NULL) return NULL;QNode* p = Q->front;CSTree T = p->data;Q->front = p->next;if (Q->front == NULL) Q->rear = NULL;free(p);return T;
}// 辅助函数：判断队列是否为空
int isQueueEmpty(Queue Q) {return Q.front == NULL;
}// 树的层次遍历
void LevelOrderTraverse(CSTree T) {if (!T) return;Queue Q;initQueue(&Q);enqueue(&Q, T);while (!isQueueEmpty(Q)) {CSTree current = dequeue(&Q);printf("%c ", current->data);// 将当前结点的所有孩子入队CSTree child = current->first_child;while (child) {enqueue(&Q, child);child = child->next_sibling;}}
}int main() {// 假设有棵树：A->B,C,D; B->E,FCSNode* A = createNode('A');CSNode* B = createNode('B');CSNode* C = createNode('C');CSNode* D = createNode('D');CSNode* E = createNode('E');CSNode* F = createNode('F');A->first_child = B;B->next_sibling = C;C->next_sibling = D;B->first_child = E;E->next_sibling = F;printf("树的层次遍历序列为：");LevelOrderTraverse(A);printf("\n");return 0;
}

运行结果：

树的层次遍历序列为：A B C D E F

森林的先序遍历

先序遍历森林的顺序是：

对森林中每一棵树，先访问树的根，然后依次先序遍历它的各个子树（从左到右），再处理森林中后面的树。

在代码实现上，通常用 孩子-兄弟（长子-右兄弟）表示法 把森林表示成一棵二叉树：

• firstchild 指向第一个孩子（对应二叉树的左孩子）
• nextsibling 指向下一个兄弟（对应二叉树的右孩子）

在这种表示法下，先序遍历非常自然：访问当前结点 → 递归遍历 firstchild → 递归遍历 nextsibling。

递归实现（最直观）

假设 T 是孩子-兄弟表示的结点指针：

void PreOrderForest(CSTree T) {if (T == NULL) return;printf("%c ", T->data);           // 访问根PreOrderForest(T->firstchild);    // 先序遍历第一个孩子（及其子树）PreOrderForest(T->nextsibling);   // 再遍历兄弟（森林中剩下的树）
}

解释：当你把森林的“第一棵树的根”传入时，这个函数会顺序访问整片森林（因为 nextsibling 会把兄弟（即森林中的后续树根）串起来）。

迭代实现（用栈 ）

思路要点：在向下沿着 firstchild 前进时，把 nextsibling（兄弟）先压栈，这样栈是 LIFO，保证我们先处理孩子，再回到兄弟。

常用写法：

void PreOrderIter(CSTree root) {if (root == NULL) return;CSTree stack[MAXN]; int top = -1;stack[++top] = root;while (top >= 0) {CSTree node = stack[top--];   // 弹出一个子树的根while (node) {printf("%c ", node->data);          // 访问当前结点if (node->nextsibling)              // 先把兄弟压栈（以后再处理）stack[++top] = node->nextsibling;node = node->firstchild;            // 向第一个孩子向下}}
}

为什么把 nextsibling 压栈？
因为我们在访问某个结点时要优先走到它的孩子，但兄弟必须在孩子处理完后再处理。把兄弟压栈就能保证“孩子先执行、兄弟后执行”。

时间复杂度：O(n)（每个结点被访问常数次）

空间复杂度（递归）：O(h)（h = 最大递归深度 = 最深的孩子链或兄弟链）

空间复杂度（迭代栈）：最坏 O(n)，平均 / 平常 O(h)

森林（两棵树）：

树1:

    A/ | \B  C  D|E

树2:

    F/ \G   H

孩子-兄弟指针关系（关键）：

• A.firstchild = B，B.nextsibling = C，C.nextsibling = D，D.firstchild = E
• A.nextsibling = F，F.firstchild = G，G.nextsibling = H

             A/ \B   F\  /C G\ \D H/E

目标输出（先序森林）： A B C D E F G H

现在用上面的迭代算法的栈状态演示（栈顶在右）：

1. 初始：push(A) → stack = [A]
2. pop -> node=A；进入内循环：
   • 访问 A (输出 A)；push(A.nextsibling=F) → stack=[F]；node=A.firstchild=B
   • 访问 B (输出 B)；push(B.nextsibling=C) → stack=[F, C]；node=B.firstchild=NULL → 内循环结束
3. pop -> node=C；内循环：
   • 访问 C (输出 C)；push(C.nextsibling=D) → stack=[F, D]；node=C.firstchild=NULL → 结束
4. pop -> node=D；内循环：
   • 访问 D (输出 D)；D.nextsibling=NULL（不压栈）；node=D.firstchild=E
   • 访问 E (输出 E)；E.firstchild=NULL → 内循环结束 → stack=[F]
5. pop -> node=F；内循环：
   • 访问 F (输出 F)；push(F.nextsibling=NULL) 无；node=F.firstchild=G
   • 访问 G (输出 G)；push(G.nextsibling=H) → stack=[H]；node=G.firstchild=NULL → 结束
6. pop -> node=H；内循环：
   • 访问 H (输出 H)；H.firstchild=NULL → 内循环结束 → stack=[]

输出序列：A B C D E F G H —— 完全正确。

森林的中序遍历

对一般树（节点可能有 ≥0 个子节点），中序遍历没有唯一的、自然的定义，因为中序原本是针对二叉树（左-根-右）设计的。但如果把森林/树用 孩子–兄弟（长子-右兄弟）表示法 转换成 二叉树 后，就可以把二叉树的中序（左 → 根 → 右）当作“森林的中序”来定义和实现。

所以这里的“森林中序”指的是：对孩子–兄弟表示的二叉树做 二叉中序。

递归定义（等价的表达式）

假设结点结构为 firstchild（左）和 nextsibling（右），则：

InOrderForest(T):if T == NULL: returnInOrderForest(T.firstchild)   // 先遍历第一个孩子（及该孩子的整片结构）visit(T)                      // 访问当前结点InOrderForest(T.nextsibling)  // 再遍历当前结点的兄弟（森林中剩下的树）

直观含义：先把当前结点的“第一个孩子的整个子树”都处理完，再访问当前结点，然后去处理当前结点的兄弟（也就是同级的下一个根/余下的森林）。

迭代实现（用栈 —— 标准二叉树中序那一套）

把 left 替换成 firstchild，right 替换成 nextsibling，就得到常见的迭代中序：

void InOrderIter(CSTree root) {if (!root) return;CSTree stack[100]; int top = -1;CSTree node = root;while (top >= 0 || node) {while (node) {stack[++top] = node;node = node->firstchild;        // 一直向第一个孩子下走（left）}node = stack[top--];                // 回溯printf("%c ", node->data);          // 访问node = node->nextsibling;           // 转向兄弟（right）}
}

时间：O(n)（每个结点被处理常数次）

空间：递归时 O(h)（h = 最大深度），迭代时栈最坏 O(n)、通常 O(h)。

森林（两棵树）：

树1:

    A/ | \B  C  D|E

树2:

    F/ \G   H

孩子–兄弟映射（左=firstchild，右=nextsibling）：

• A.left = B，B.right = C，C.right = D，D.left = E
• A.right = F，F.left = G，G.right = H

         A/ \B   F\  /C G\ \D H/E

用上面递归/迭代规则，中序输出为：
B C E D A G H F

用迭代算法的栈跟踪（栈顶在右边）：

初始：node=A, stack=[], output=[]

1. 向下压左链：push A，node=B → push B，node=NULL
   stack=[A,B], output=[]
2. pop B，visit B → output=[B]，node=B.nextsibling=C
3. push C，node=NULL → pop C，visit C → output=[B,C]，node=C.nextsibling=D
4. push D，node=D.firstchild=E → push E，node=NULL
5. pop E，visit E → output=[B,C,E]，node=E.nextsibling=NULL
6. pop D，visit D → output=[B,C,E,D]，node=D.nextsibling=NULL
7. pop A，visit A → output=[B,C,E,D,A]，node=A.nextsibling=F
8. push F，node=F.firstchild=G → push G，node=NULL
9. pop G，visit G → output=[B,C,E,D,A,G]，node=G.nextsibling=H
10. push H，node=NULL → pop H，visit H → output=[B,C,E,D,A,G,H]，node=H.nextsibling=NULL
11. pop F，visit F → output=[B,C,E,D,A,G,H,F]，结束

结果同上：B C E D A G H F。