当前位置：首页 > news >正文

数学建模模型

news 2025/8/28 5:31:39

一、评价决策类

1、层次分析法

1.数据归一化处理：指标的数组[a b c] 归一化处理得到[a/(a+b+c)]，b/(a+b+c),c/(a+b+c)]
2.来给每一个指标加上权重，并用归一化后的变量 * 权重

基本步骤：

构造出各层种的所有判断矩阵

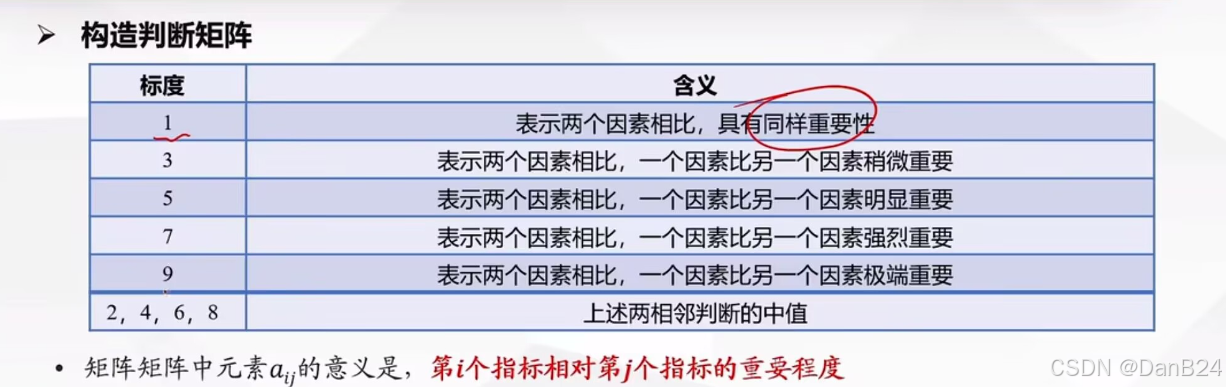
对指标种的重要性进行两两比较，构造判断矩阵，从而科学的求出权重
矩阵中元素aij 的意思是：第i个指标相对第j个指标的重要程度

在这里插入图片描述

2.Topsis法（优劣解距离法）

TOPSIS法引入了两个基本概念:
- 理想解:设想的最优的解(方案)，它的各个属性值都达
  到各备选方案中的最好的值;
- 负理想解:设想的最劣的解(方案)，它的各个属性值都
  达到各备选方案中的最坏的值。
- 方案排序的规则是把各备选方案与理想解和负理想解做
  比较，若其中有一个方案最接近理想解，而同时又远离负理
  想解，则该方案是备选方案中最好的方案。TOPSIS通过最接
  近理想解且最远离负理想解来确定最优选择
模型原理：
TOPSIS法是一种理想目标相似性的顺序选优技术,在多目标决策分析中是一种非常有效的方法,它通过归一化后(去量纲化)的数据规范化矩阵，找出多个目标中最优目标和最劣目标(分别用理归想一解化和反理想解表示),分别计算各评价目标与理想解和反理想解的距离,获得各目标与理想解的贴近度,按理想解贴近度的大小排序,以此作为评价目标优劣的依据。贴近度取值在0~1之间,该值愈接
近1,表示相应的评价目标越接近最优水平:反之,该值愈接近0.表示评价目标越接近最劣水平，在多目标角色分析中是非常有效

在这里插入图片描述

3.熵权法

在层次分析法和TOPSIS法中的权重都是客观得到的（主观评价、查文献、专家打分），那么熵权法计算比较客观的方法。

熵权法，物理学名词，按照信息论基本原理的解释，信息是系统有序程度的一个度量，是系统无序程度的一个度量:根据信息熵的定义，对于某项指标，可以用熵值来判断某个指标的离散程度，其信息熵值越小，指标的离散程度越大，该指标对综合评价的影响(即权重)就越大，如果某项指标的值全部相等，则该指标在综合评价中不起作用。因此，可利用信息这个工具，计算出各个指
标的权重，为多指标综合评价提供依据。
熵权法是一种客观的赋权方法，它可以靠数据本身得出权重

依据的原理:指标的变异程度越小，所反映的信息量也越少，其对应的权值也应该越低
在这里插入图片描述


import pandas as pd
import numpy as np
import matplotlib.pyplot as plt# 从Excel文件中读取数据
file_path = r'D:\py\LearnPython\data.xlsx'
data = pd.read_excel(file_path)# 数据标准化为极大型指标
def standardize_data(df, min_columns):for column in df.columns:max_val = df[column].max()min_val = df[column].min()if column in min_columns:  # 极小型指标df[column] = (max_val - df[column]) / (max_val - min_val)else:  # 极大型指标df[column] = (df[column] - min_val) / (max_val - min_val)return df# 计算熵权
def calculate_entropy_weights(df):prob_matrix = df.div(df.sum(axis=0), axis=1)entropy = -np.sum(prob_matrix * np.log(prob_matrix + np.finfo(float).eps), axis=0) / np.log(len(df))weights = (1 - entropy) / (1 - entropy).sum()return weights# 执行TOPSIS算法
def topsis(df, weights):normalized_df = df.div(np.sqrt((df ** 2).sum(axis=0)), axis=1)weighted_normalized_df = normalized_df.mul(weights, axis=1)ideal_best = weighted_normalized_df.max()ideal_worst = weighted_normalized_df.min()distance_to_best = np.sqrt(((weighted_normalized_df - ideal_best) ** 2).sum(axis=1))distance_to_worst = np.sqrt(((weighted_normalized_df - ideal_worst) ** 2).sum(axis=1))relative_closeness = distance_to_worst / (distance_to_best + distance_to_worst)return relative_closeness# 从用户输入中获取极小型指标的列索引
min_columns_input = input("请输入极小型指标的列索引，用空格分隔: ").split()
min_columns_index = [int(i) for i in min_columns_input]  # 将输入的列索引直接使用# 根据索引获取极小型指标的列名
min_columns = [data.columns[i-1] for i in min_columns_index]# 主流程
standardized_data = standardize_data(data.copy(), min_columns)
weights = calculate_entropy_weights(standardized_data)# 确保所有列的权重都被计算
weights_series = pd.Series(weights, index=standardized_data.columns)topsis_scores = topsis(standardized_data, weights)# 添加TOPSIS得分到原始数据
data['TOPSIS_Score'] = topsis_scores# 保存结果
output_path = 'processed_data_with_topsis.xlsx'
data.to_excel(output_path, index=False)# 可视化
plt.figure(figsize=(12, 8))
plt.bar(range(1, len(data) + 1), data['TOPSIS_Score'], color='skyblue')
plt.xlabel('Sample Index')
plt.ylabel('TOPSIS Score')
plt.title('TOPSIS Scores of Samples')
plt.xticks(range(1, len(data) + 1))
plt.grid(True)
plt.tight_layout()
plt.savefig('topsis_scores.png', format='png', dpi=300)
plt.show()print("数据已处理并保存至:", output_path)
print("条形图已保存至 topsis_scores.png")
print("权重是：")
for col, weight in weights_series.items():print(f'{col}: {weight}')