并行多核体系结构基础——共享存储并行编程（笔记）

三、共享存储并行编程

3.1 并行编程步骤

依靠算法/代码：

1. 识别并行任务
2. 确定变量范围（小任务合并为大任务）
3. 必要的话插入同步

（机器独立）

---

（机器依赖）

4. 将任务分配给线程
5. 将线程映射到处理器

3.2 依赖分析

$S$表示一个语句或者一组语句。$S1\to S2$表示程序执行中，$S1$先于$S2$出现，那么：

• $S1{\to }^{T}S2$：表示真依赖，即$S1$写入$S2$读取位置
• $S1{\to }^{A}S2$：表示反依赖，即$S1$读取$S2$写入位置
• $S1{\to }^{O}S2$：表示输出依赖，即$S1$写入$S2$写入的同一位置

S1 x = 2;
S2 y = x;
S3 y = x + z;
S4 z = 6;

上述逻辑中，

• $S1{\to }^{T}S2$
• $S1{\to }^{T}S3$
• $S3{\to }^{A}S4$
• $S2{\to }^{O}S3$

反依赖与输出依赖又称为假依赖，后续指令不依赖于先前指令产生的任何值，并行程序中消除假依赖一般通过私有化。
真依赖一般难以消除，他们是并行化的障碍。

3.2.1 循环级依赖分析

定义$[i,j]$表示循环迭代空间。循环上层迭代$i$次，内存循环迭代$j$次。

for(i=1;i<n;i++){
S1: a[i] = a[i-1] + 1;
S2: b[i] = a[i];
}
for(i=1;i<n;i++)for(j=1;j<n;j++)S3: a]i][j] = a[i][j-1] + 1;
for(i=1;i<n;i++)for(j=1;j<n;j++)S4: a]i][j] = a[i-1][j] + 1;

依赖关系如下：

• $S1[i]{\to }^{T}S1[i+1]$
• $S1[i]{\to }^{T}S2[i]$
• $S3[i,j]{\to }^{T}S3[i,j+1]$
• $S4[i,j]{\to }^{T}S4[i+1,j]$

3.2.2 迭代空间遍历图和循环传递依赖图

迭代空间遍历图（ITG）：以图形方式展示了迭代空间中的遍历顺序，不显示依赖性。

循环传递依赖图（LDG）：以图形方式展示了真/反/输出依赖，其中一个节点就是迭代空间中的一个点，而有向边显示依赖的方向。

for(i=1;i<4;i++)for(j=1;j<4;j++)S1: a]i][j] = a[i][j-1] + 1;

依赖关系为：$S1[i,j]{\to }^{T}S1[i,j+1]$
ITG

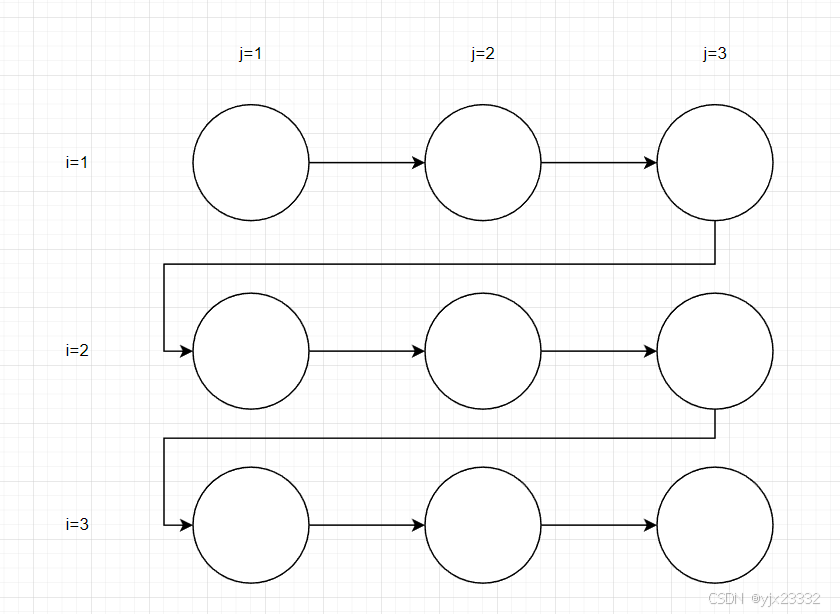
LDG

其中$\to$为真依赖

for(i=1;i<=n;i++)for(j=1;j<=n;j++)S1: a]i][j] = a[i][j-1] + a[i][j+1] + a[i-1][j] + a[i+1][j];

依赖关系为：

• $S1[i,j]{\to }^{T}S1[i,j+1]$
• $S1[i,j]{\to }^{T}S1[i+1,j]$
• $S1[i,j]{\to }^{A}S1[i,j+1]$
• $S1[i,j]{\to }^{A}S1[i+1,j]$

注意，我们始终注意的是$S$读取和写入的位置，即i,j始终表示的是等号左侧的值。
因此$S1[i,j]$（我们设它为$x$）的值会在$S1[i,j+1]$与$S1[i+1,j]$被读取（等号左侧）
而此时x对应的等号右侧$S1[i,j+1]$与$S1[i+1,j]$的值未被赋值，他们将会在等号左侧（相对当前i,j）为$S1[i,j+1]$与$S1[i+1,j]$时读取$x$的值.

ITG

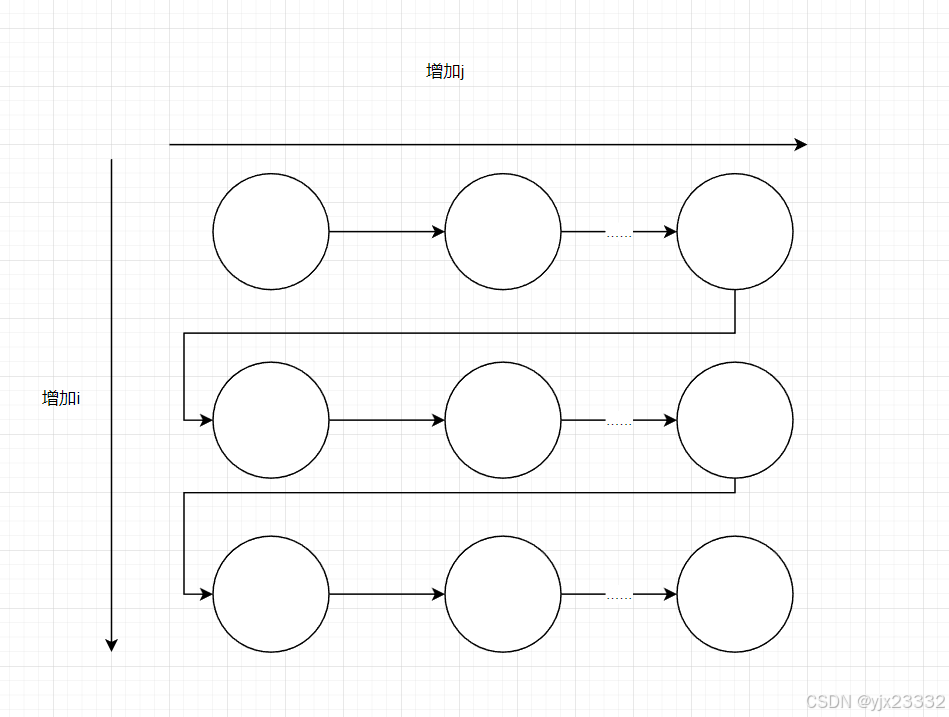
LDG

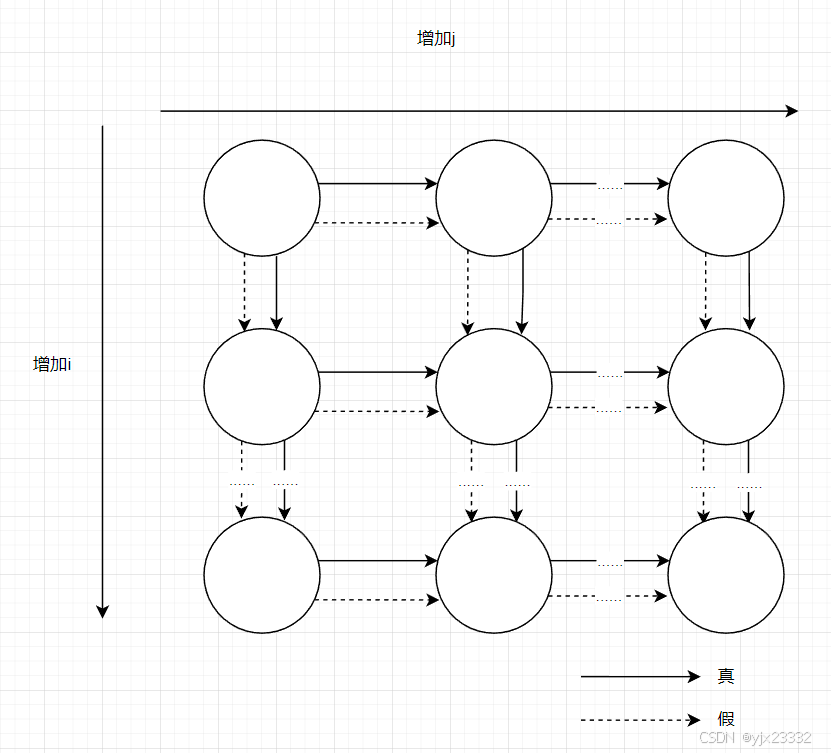
3.3 识别循环依赖中的并行任务

3.3.1 循环迭代间的并行和DOALL并行

for(i=2;i<=n;i++)S1: a]i] = a[i-2];

依赖关系为：

• $S1[i]{\to }^{T}S1[i+2]$

LDG

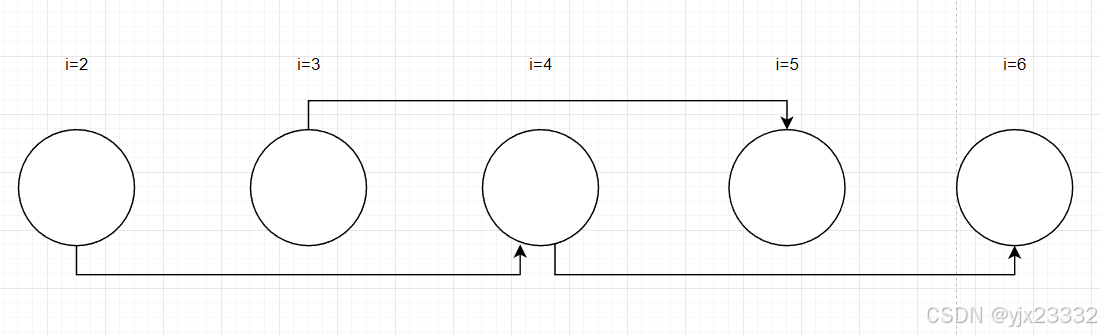
很容易发现，整个循环偶数和奇数各走各的，因此可以拆为两个并行循环。

• DOALL并行

当一个循环的所有迭代都是可并行的任务时（以某种循环执行时，循环流程中无黑实线），则该循环表现出DOALL并行。

for(i=1;i<=n;i++)for(j=1;j<=n;j++)S1: a]i][j] = a[i][j-1] + a[i][j+1] + a[i-1][j] + a[i+1][j];

这个LDG途中，以反对角线的方式进行循环将无黑实线

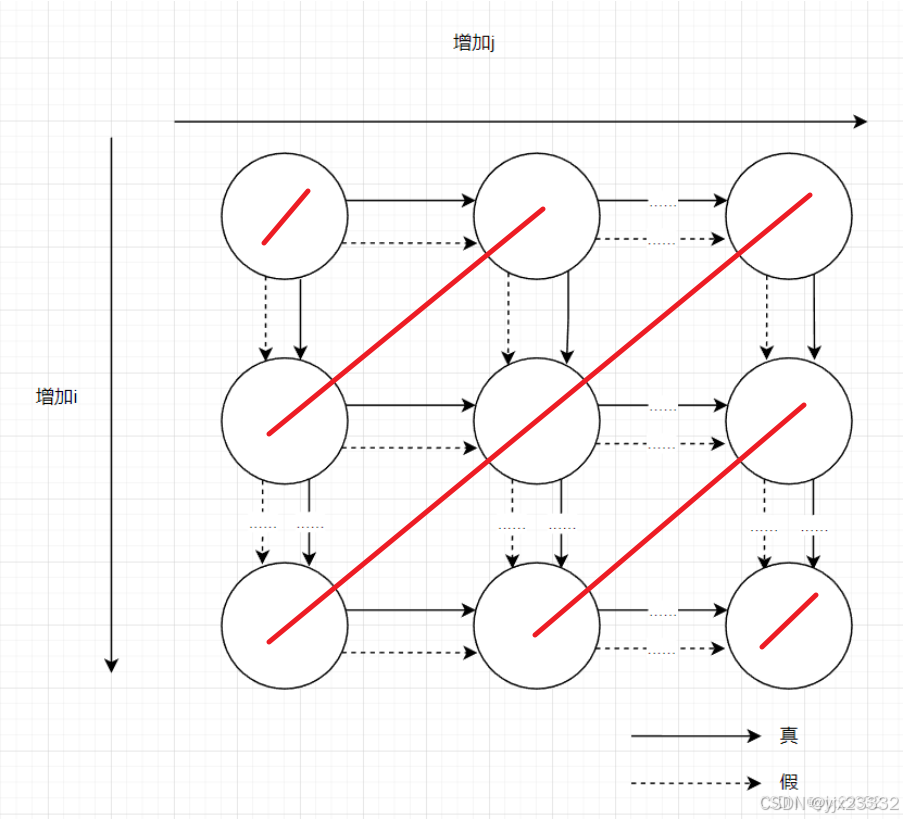
3.3.2 DOACROSS：循环迭代间的同步并行

因为DOALL并行循环中并行任务数量非常大，因此优先识别。

for(i=1;i<=N;i++)
S: a[i] = a[i-1] + b[i] * c[i];

依赖关系为：
$S[i]{\to }^{T}S[i+2]$

由于不能用DOALL并行，但是$b$和$c$没有参与循环，于是我们可以将其拆分为：

for(i=1;i<=N;i++)// DOALL并行
S1: temp[i] = b[i] * c[i];
for(i=1;i<=N;i++)
S2: a[i] = a[i-1] + temp[i];

• DOACROSS并行
  在具有部分循环依赖的循环中提取并行任务的解决方案是采用DOACROSS并行。其中每个迭代仍是并行任务，但是插入了同步以确保【使用者迭代】（consumer iteration）只读取【产生者迭代】（producer iteration）产生的数据。

上述式子优化后，可为：

post(0);
for(i=1;i<=N;i++){
S1: temp[i] = b[i] * c[i];
wait(i-1);
S2: a[i] = a[i-1] + temp[i];
post(i);
}

在所有循环都并行中，i次循环通过wait()等待i-1次循环执行完成，并将自己执行完成的值放入post()激活i+1次循环。

我们假设同步延迟为0，$T_{S1}$与$T_{S2}$分别表示语句$S1$与$S2$的执行时间。

顺序执行总时间为：
$$N\ast (T_{S1}+T_{S2})$$
DOACROSS并行总时间为：
$$T_{S1}+N\ast T_{S2}$$
即加速比：
$$\frac{N\ast (T_{S1}+T_{S2})}{T_{S1}+N\ast T_{S2}}$$
$$1+\frac{1-\frac{1}{N}}{\frac{1}{N}+\frac{T_{S2}}{T_{S1}}}$$

N趋向无穷后，最终耗时可以简化为
$$1+\frac{T_{S1}}{T_{S2}}$$

由此可知实际改进了多少，取决于并行部分和串行部分的耗时比，以及同步时间。由于同步开销通常很大，使用DOACROSS并行时，尽量将许多同步任务放到同一个线程中，减少同步次数。

3.3.3 循环中语句间的并行

当一个循环具有循环传递依赖时，另一种并行化的方法是将一个循环分发（distribute）到几个循环中去。

for(i=1;i<=n;i++){
S1: a[i] = b[i+1]*a[i-1];
S2: b[i] = b[i]*coef;
S3: c[i] = 0.5*(c[i]+a[i]);
S4: d[i] = d[i-1]*d[i];
}

依赖为：

• $S1[i]{\to }^{T}S1[i+1]$
• $S4[i]{\to }^{T}S4[i+1]$
• $S1[i]{\to }^{A}S2[i+1]$
• $S1[i]{\to }^{T}S3[i]$

依据上可得，S4可以单独提出来，改为：

for(i=1;i<=n;i++){//循环1
S1: a[i] = b[i+1]*a[i-1];
S2: b[i] = b[i]*coef;
S3: c[i] = 0.5*(c[i]+a[i]);
}for(i=1;i<=n;i++){//循环2
S4: d[i] = d[i-1]*d[i];
}

我们假设，$T_{S1}$、$T_{S2}$、$T_{S3}$、$T_{S4}$分别表示语句$S1$、$S2$、$S3$、$S4$的执行时间。
加速比就为：

$$\frac{N\ast (T_{S1}+T_{S2}+T_{S3}+T_{S4})}{max(N\ast (T_{S1}+T_{S2}+T_{S3}),N\ast T_{S4})}$$

如果$T_{S1}$、$T_{S2}$、$T_{S3}$、$T_{S4}$均为$T$，则结果为：
$$\frac{N\ast (T_{S1}+T_{S2}+T_{S3}+T_{S4})}{max(N\ast (T_{S1}+T_{S2}+T_{S3}),N\ast T_{S4})}=\frac{4NT}{max(3NT,NT)}=\frac{4}{3}$$

注意到，$S1[i]{\to }^{T}S1[i+1]$执行完成后，$S1[i]{\to }^{A}S2[i+1]$与$S1[i]{\to }^{T}S3[i]$可以DOALL并行。

可调整代码为：

for(i=1;i<=n;i++){//并行循环1
S1: a[i] = b[i+1]*a[i-1];
}for(i=1;i<=n;i++){//并行循环1
S4: d[i] = d[i-1]*d[i];
}// 并行循环1结束后，再执行如下循环
for(i=1;i<=n;i++){//并行循环2
S2: b[i] = b[i]*coef;
}for(i=1;i<=n;i++){//并行循环2
S3: c[i] = 0.5*(c[i]+a[i]);
}

如果$T_{S1}$、$T_{S2}$、$T_{S3}$、$T_{S4}$均为$T$，此时加速比为：
$$\frac{N\ast (T_{S1}+T_{S2}+T_{S3}+T_{S4})}{max(N\ast T_{S1}+max(T_{S2},T_{S3}),N\ast T_{S4})}=\frac{4NT}{max((N+1)T,NT)}=\frac{4NT}{(N+1)T}$$

3.3.4 DOPIPE循环中语句间的流水线并行

如果存在传递依赖的情况，可以使用流水线并行：

for(i=1;i<=n;i++){
S1: a[i] = a[i-1]+b[i];
S2: c[i] = c[i]+a[i];
}

依赖为：

• $S1[i]{\to }^{T}S1[i+1]$
• $S1[i]{\to }^{T}S2[i]$

那么通过DOPIPE并行，可以改为：

for(i=1;i<=n;i++){
S1: a[i] = a[i-1]+b[i];
post(i);
}for(i=1;i<=n;i++){
wait(i);
S2: c[i] = c[i]+a[i];
}

3.3.3中的例子

for(i=1;i<=n;i++){
S1: a[i] = b[i+1]*a[i-1];
S2: b[i] = b[i]*coef;
S3: c[i] = 0.5*(c[i]+a[i]);
S4: d[i] = d[i-1]*d[i];
}

DOPIPE并行的话，可以改为：

post(0);
for(i=1;i<=n;i++){//循环1
S1: a[i] = b[i+1]*a[i-1];
post(i);
}for(i=1;i<=n;i++){//循环2
S4: d[i] = d[i-1]*d[i];
}for(i=1;i<=n;i++){//循环3
wait(i-1);
S2: b[i] = b[i]*coef;
}for(i=1;i<=n;i++){//循环4
wait(i);
S3: c[i] = 0.5*(c[i]+a[i]);
}

为减少DOPIPE并行的同步开销，我们可以每n次迭代后再post()一次，而不是每完成一次循环就同步一次

3.4 识别其他层面的并行

在针对非循环的程序逻辑中，我们可以将代码分成三组语句：

1. 函数调用之前（前置代码）
2. 要调用的每个函数（函数）
3. 调用函数之后（后置代码）

这三个代码间若缺少真依赖都会为并行带来机会。

int search_tree(struct tree *p,int data){
S1:int count = 0;if(p == NULL){return 0;}if(p->data == data){count = 1;}
S2:	count += search_tree(p->left);
S3:	count += search_tree(p->right);
S4:	return count;
}

依赖为：

• $S1{\to }^{T}S2$
• $S1{\to }^{T}S3$
• $S1{\to }^{T}S4$
• $S2{\to }^{T}S3$
• $S2{\to }^{T}S4$
• $S3{\to }^{T}S4$

通过重命名的方式，我们可以将依赖消减为：

int search_tree(struct tree *p,int data){
S1:	int count = 0;if(p == NULL){return 0;}if(p - data == data){count = 1;}
S2:	int count2 += search_tree(p->left);
S3:	int count3 += search_tree(p->right);
S4:	return (count1 + count2 + count3);
}

依赖为：

• $S1{\to }^{T}S4$
• $S2{\to }^{T}S4$
• $S3{\to }^{T}S4$

此时S1、S2与S3就可以单独执行了

3.5 确定变量的范围

确定并行任务后，通常并行任务数量多于可用的处理器数量，因此多个任务再分配给线程执行之前经常会合并为较大任务。执行任务的线程数通常等于或小于可用处理器数量。本节先假设处理器数目无限。

将变量分为如下几类：

• 只读
• 读/写非冲突
• 读/写冲突

3.5.1 私有化

读/写冲突的变量阻碍并行，对此最主要就是将他们私有化。

可私有化的变量：

1. 在原始顺序程序执行次序中，变量由一个任务首先定义（或写入），然后才能被该任务使用（读取）。
2. 变量在被同一个任务读取之前没有被定义，但是任务应该从变量中读取的值是事先知道的。

3.5.2 归约变量和操作

归约是指将多个并行任务的私有化计算结果合并以形成最终结果。

3.5.3 准则

• 只读变量应声明为共享，避免可能降低性能的存储开销。
• 读/写非冲突变量也应声明为共享
• 读/写冲突的变量通常也应该声明为共享，但是要用临界区保护对它的访问（临界区是昂贵的），需要衡量私有化和临界区的代价。

临界区：
一次仅允许一个进程使用的共享资源

3.6 同步

同步操作不在任务间执行，而是在线程间。

同步的方式

1. 点对点同步：提交与等待的方式。等待线程会阻塞，直到对应的标记被提交后，才会继续执行（上述的DOACROSS与DOPIPE并行）
2. 锁同步：通过获取锁与释放锁的方式（排他锁），保证执行顺序。
3. 栅障：定义了一个点，所有线程都达到时才允许线程通过。（Java中的 CyclicBarrier和CountDownLatch）

3.7 任务到线程的映射

3.7.1 静态与动态分配

分配方式：

1. 静态分配：执行之前将任务固定分配给线程
2. 动态分配：任务在执行之前是不会分配给线程，依据线程是否空闲分配任务（线程池）。这会给任务队列管理带来额外开销

块大小：代表单个任务的连续迭代数量。

为了说明静态分配，我们假设总迭代数目：$n=8$，线程数：$p=2$，

sum = 0;
for(i=0;i<n;i++){for(j=0;j<=i;j++){sum += a[i][j];}
}
Print sum;

如果块大小为4时，线程1执行外层前4个迭代，线程2执行外层后4个迭代。

• 线程1的内层循环次数为：$1+2+3+4=10$(因为内嵌循环j<=i，j随着i的增大而增大)
• 线程2的内层循环次数为：$5+6+7+8=26$(因为内嵌循环j<=i，j随着i的增大而增大)

出现了不均衡调度。

但如果将块大小缩小至1，线程1执行外层奇数迭代，线程2执行外层偶数迭代。

• 线程1的内层循环次数为：$1+3+5+7=16$
• 线程2的内层循环次数为：$2+4+6+8=20$

不均衡有所缓减，因此如果循环迭代较多时，可以适当减小块大小。

3.7.2 固有通信与人为通信

1. 固有通信：任务映射对算法影响，主要体现算法本身对于通信的需求
2. 人为通信：任务映射对数据布局方式和架构影响，依赖于核的并行架构（基本可以认为是硬件层级）

固有通信的评估可以用：
$$通信-计算比率（CCR）$$
$$CCR=\frac{线程通信量（单个线程对其他线程访问量）}{单个线程计算量（\frac{输入规模}{处理器数量}）}$$

人为通信：需要考虑在两个处理器之间来回交换数据。受数据交换频率和数据交换延迟影响。

3.8 线程到处理器的映射

最简单的方式为让操作系统线程调度器自己决定。但针对并行程序，要确保它的所有线程同时运行或这都不运行，来减少阻塞耗费的时间。

一些操作系统有成组调度功能，一组中的线程会被同时调度运行和等待。

此外将线程映射到处理器也是为了数据局部性，避免数据存储位置距离核较远问题。通过数据映射和线程到处理器的显式映射的方式解决。

• 数据映射的方式，有如下实现方式
  • 允许将数据分配或映射到访问该数据的线程所运行的节点。（比如C就可以）
  • 分配或迁移数据到访问该数据的线程。
• 线程到处理器的显式映射的方式则依赖于操作系统提供的接口
  • 比如linux的cset或者C在windows中的SetThreadAffinityMask(handle, mask)。

3.9 OpenMP概述

开放式多处理（Open Multi-Processing）是支持共享存储编程的应用编程接口（API）。

它支持C、C++和Fortran语言。通过OpenMP，开发者可以编写能够在多核心、多处理器计算机上高效运行的并行程序。OpenMP通过提供高层抽象的并行算法描述，降低了并行编程的难度和复杂度。当编译器不支持OpenMP时，程序会退化成普通（串行）程序，而程序中已有的OpenMP指令不会影响程序的正常编译运行。

也就是一套封装好的框架，可以较方便让程序有并行功能。

具体可以参考OpenMp

参考文献

【1】《并行多核体系结构基础》【美】汤孟岩
【2】OpenMp