CF2133C 下界(The Nether)
CF2133C 下界(The Nether)
洛谷题目传送门
题目描述
这是一道交互题。
最近发现下界(The Nether)后,Steve 在他的世界中建造了一个由 nnn 个下界传送门组成的网络,每个传送门位于不同的位置。
每个传送门都单向连接到若干(可能为零)其他传送门。为避免迷路,Steve 精心构建了这个传送门网络,确保不存在通过传送门跳跃能从某个位置回到自身的情况;严格来说,该网络构成一个有向无环图(DAG)。
Steve 拒绝告诉你哪些传送门相互连接,但允许你进行查询。每次查询时,你给 Steve 一个位置集合 S={s1,s2,…,sk}S = \{s_1, s_2, \ldots, s_k\}S={s1,s2,…,sk} 和一个起始位置 x∈Sx \in Sx∈S。Steve 会找出从 xxx 出发、仅经过 SSS 中位置的最长路径,并告诉你该路径经过的位置数量(若无法从 xxx 到达 SSS 中任何其他位置,Steve 会回复 111)。
由于你希望获得“热门景点成就,你需要找到一条访问尽可能多位置的路径。Steve 特别慷慨,允许你使用最多 2⋅n2 \cdot n2⋅n 次查询来找出答案。
输入格式
每个测试包含多个测试用例。第一行包含测试用例数量 ttt(1≤t≤10001 \le t \le 10001≤t≤1000)。接下来描述每个测试用例。
每个测试用例仅有一行,包含一个整数 nnn(2≤n≤5002 \le n \le 5002≤n≤500)——表示位置数量。
保证所有测试用例的 n3n^3n3 之和不超过 5003500^35003。
输出格式
无
输入输出样例 #1
输入 #1
2
53321211
输出 #1
? 1 4 1 2 3 4? 3 3 4 3 2? 5 2 1 5? 2 2 2 4! 4 5 1 4 2? 1 2 1 2? 2 2 1 2! 1 1
说明/提示
第一个测试用例中,传送门网络结构如下:
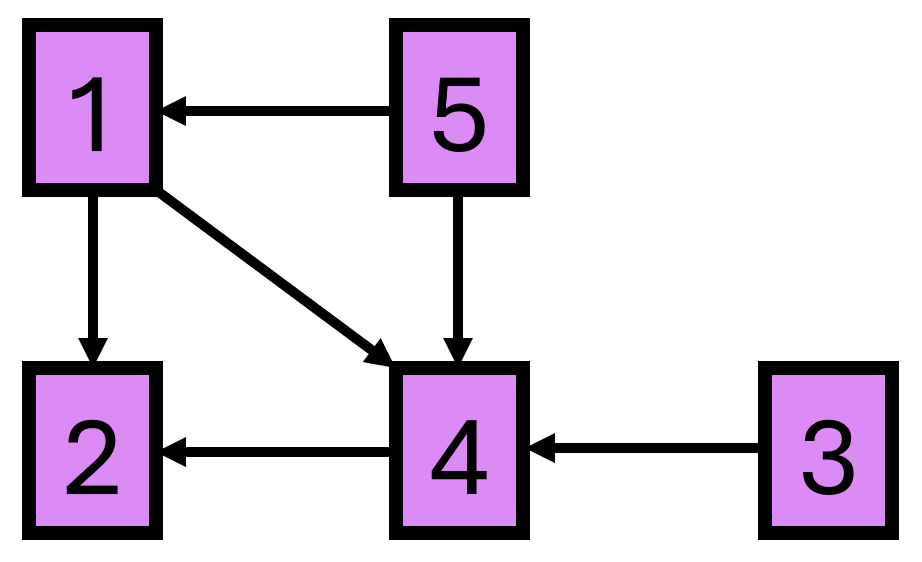
- 从位置 111 出发、仅经过集合 {1,2,3,4}\{1, 2, 3, 4\}{1,2,3,4} 的最长路径是 1→4→21 \rightarrow 4 \rightarrow 21→4→2,该路径包含 333 个不同位置。
- 从位置 333 出发、仅经过集合 {2,3,4}\{2, 3, 4\}{2,3,4} 的最长路径是 3→4→23 \rightarrow 4 \rightarrow 23→4→2,该路径包含 333 个不同位置。
- 从位置 555 出发、仅经过集合 {1,5}\{1, 5\}{1,5} 的最长路径是 5→15 \rightarrow 15→1,该路径包含 222 个不同位置。
- 从位置 222 出发无法到达集合 {2,4}\{2, 4\}{2,4} 中的任何其他位置,因此 Steve 对该查询回复 111。
利用这些查询信息,可确定最长路径为 5→1→4→25 \rightarrow 1 \rightarrow 4 \rightarrow 25→1→4→2。
第二个测试用例中,传送门网络结构如下:
两个传送门之间没有相互连接,因此最长路径仅包含单个位置。注意:输出 ! 1 2 同样是一个有效答案。
思路详解
题目分析
我们有2N2N2N词的询问机会,思考如何求出最长路及最长路上的节点???如果只是求最长路,我们只需要以每个节点为起点,让SSS包含所有节点,询问NNN次即可。可是如何求出最长路上的节点呢?求最长路长度的询问次数肯定变不了,我们一定要在NNN询问以内求出最长路上的节点。
我们返现我们通过询问最长路长度可以知道最长路的起点,考虑如何求出其他节点?我们发现对于两个点u,vu,vu,v如果有一条边u−>vu->vu−>v,则询问 ? u 2 u v 的答案必定为2。那我们难道要从起始节点将这个图还原出来?显然我们没有N2N^{2}N2的询问次数。
我们发现若从最长路起点uuu开始的最长路长度为lenlenlen,则uuu在最长路上的下一个节点vvv,从vvv开始的最长路的长度必定为len−1len-1len−1。
那我们每次只需要去询问最长路长度为len−1len-1len−1的节点vvv是否与节点uuu相连,相连则在找与vvv相连的…最后找到的节点len=1len=1len=1。
过程分析
我们的具体过程如下:
- 首先进行NNN次询问求解最长路及其起点。
- 在依次寻找最长路上的其他节点。
- 最后输出答案即可。
code
#include<bits/stdc++.h>
using namespace std;
int T;
const int N=505;
struct node{int x,id;friend bool operator<(node t1,node t2){return t1.x>t2.x;}
}js[N];
int ans[N];
int main(){
//根据题目,我们可以提问2n次,我们需要求出最长路及最长路上的节点
//考虑先询问n次求出最长路,并记录从每个点开始的最长路
//我们找到了最长路的长度和最长路的起始点,考虑如何求出其他点
//我们发现,若有一条边u->v,则询问? u 2 u v必定为2
//所以我们可以一次遍历当前最长路长度i,寻找节点的最长路为i-1且这两点相连,这个节点即为当前节点在最长路中的上一个节点cin>>T;while(T--){int n;cin>>n;for(int i=1;i<=n;i++){cout<<'?'<<' '<<i<<' '<<n<<' ';for(int j=1;j<=n;j++)cout<<j<<' ';cout<<'\n';cout.flush();//询问每个节点的最长路径int x;cin>>x;js[i].x=x;js[i].id=i;//记录}sort(js+1,js+1+n);int beg=js[1].id,o=1;//取最长路径ans[o]=js[1].id;for(int i=js[1].x-1;i>=1;i--){//遍历最长路的长度for(int j=1;j<=n;j++){if(js[j].x==i){cout<<'?'<<' '<<beg<<' '<<2<<' '<<beg<<' '<<js[j].id<<'\n';cout.flush();//询问判断两个节点是否相连int x;cin>>x;if(x==2){beg=js[j].id;break;}}}ans[js[1].x-i+1]=beg;//记录当前节点}cout<<'!'<<' '<<js[1].x<<' ';//输出答案for(int i=1;i<=js[1].x;i++)cout<<ans[i]<<' ';cout<<'\n';cout.flush();}return 0;
}
