LeetCode 100题（3）（10题）

1：141. 环形链表 - 力扣（LeetCode）

题意：给定一个链表，判断其是否有环，有环则返回true，反之则返回 false

思路：设定两个指针，一个快指针，一个慢指针，快指针每次走两个单位长度，慢指针每次走一个单位长度，如果最后它们能相遇则说明是有环的。

/*** Definition for singly-linked list.* class ListNode {*     int val;*     ListNode next;*     ListNode(int x) {*         val = x;*         next = null;*     }* }*/
public class Solution {public boolean hasCycle(ListNode head) {ListNode slow=  head;ListNode fast = head;while(fast != null){slow = slow.next;if(fast.next != null) fast = fast.next.next;else return false;if(fast == slow) return true;}return false;}
}

2：139. 单词拆分 - 力扣（LeetCode）

题意：给定一个字符串 S，和一个字符串数组，问你能不能用数组里面的字符串组成 S，可以则返回 true，反之返回 false;

思路：很经典的一道题目，我们首先用 set集合 将数组里面的字符串字符串存进去，然后要用到动态规划的思想，f[i] 的状态表示是：在S中，从第一个字母到第i个字母是否能够凑出来，状态转移见代码，还是比较好理解的

class Solution {public boolean wordBreak(String s, List<String> wordDict) {Set<String> set = new HashSet<>(wordDict);int maxn = 0;for(String ss : wordDict){maxn = Math.max(maxn, ss.length());}int n = s.length();boolean[] f = new boolean[n + 1];f[0] = true;for(int i = 1; i <= n; i ++){for(int j = i - 1; j >= Math.max(0, i - maxn); j --){if(f[j] && set.contains(s.substring(j, i))){f[i] = true;break;}}}return f[n];}
}

3：136. 只出现一次的数字 - 力扣（LeetCode）

题意：给定一个数组，其中某个元素只出现一次，别的元素都会出现两次，让你找出那个只出现一次的元素

思路：常规思路就是用 HashMap 来存每个元素出现的次数，就不多说了，最简单最快的做法是用位运算来考虑，因为两个相同的元素异或出来是0，所以这里面的每对相同的元素都会两两抵消成0，而最后0再和那个只出现一次的元素异或，最后答案就是那个只出现一次的元素。

class Solution {public int singleNumber(int[] nums) {// int n = nums.length;// Map<Integer, Integer> mp = new HashMap<>();// for(int i = 0; i < n; i ++){//     if(mp.containsKey(nums[i])){//         int cnt = mp.get(nums[i]);//         mp.put(nums[i], cnt + 1);//     }else{//         mp.put(nums[i], 1);//     }// }// for(Integer num : mp.keySet()){//     int cnt = mp.get(num);//     if(cnt == 1){//         return num;//     }// }// return -1;int ans = 0;for(int num : nums){ans ^= num;}return ans;}
}

4：647. 回文子串 - 力扣（LeetCode）

题意：给定一个字符串，判断其中回文子串的个数

思路：也是比较经典的问题，考虑dp，设 dp[i][j]，状态表示为：索引 i 到 索引 j 是否为回文子串，状态转移方程见代码，还是比较好理解的，当然官方还给了一个中心拓展法，时间复杂度是更优的，但是我个人是比较讨厌这种找规律找出来的方法

class Solution {public int countSubstrings(String s) {//1：动态规划法int n = s.length();int ans = 0;boolean[][] dp = new boolean[n + 1][n + 1];for(int j = 0; j < n; j ++){for(int i = 0; i <= j; i ++){if(s.charAt(i) == s.charAt(j) && (j - i < 2 || dp[i + 1][j - 1])){dp[i][j] = true;ans ++;}}}return ans;//2：中心扩展法//     for(int i = 0; i < n * 2 - 1; i ++){//         int left = i / 2;//         int right = left + (i % 2);//         while(left >= 0 && right < n && s.charAt(left) == s.charAt(right)){//             ans ++;//             left --;//             right ++;//         }//     }//     return ans;}
}

5：128. 最长连续序列 - 力扣（LeetCode）

题意：给定一个未排序的整数数组，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。

思路：我还是选择用 dp 来做，因为题目的意思是忽略原数组中数字的索引，所以我们可以直接排序，dp[i]的状态表示为：截止到索引 i ，这个索引位置能凑出的最优解，状态转移见代码，还是比较简单的

class Solution {public int longestConsecutive(int[] nums) {int n = nums.length;if(n == 0){return 0;}int ans = 1;Arrays.sort(nums);int[] dp = new int[n];dp[0] = 1;for(int i = 1; i < n; i ++){if(nums[i] - nums[i - 1] == 1){dp[i] = dp[i - 1] + 1;}else if(nums[i] == nums[i - 1]){dp[i] = dp[i - 1];}else{dp[i] = 1;}ans = Math.max(ans, dp[i]);}return ans;}
}

6：124. 二叉树中的最大路径和 - 力扣（LeetCode）

题意：给定一个二叉树，让你算出它的最大路径和，说的通俗点，这里的路径就是不能走回头路，也就是一笔到底，一个点不能走两遍，我一开始就是没审清题目的意思卡了好久；

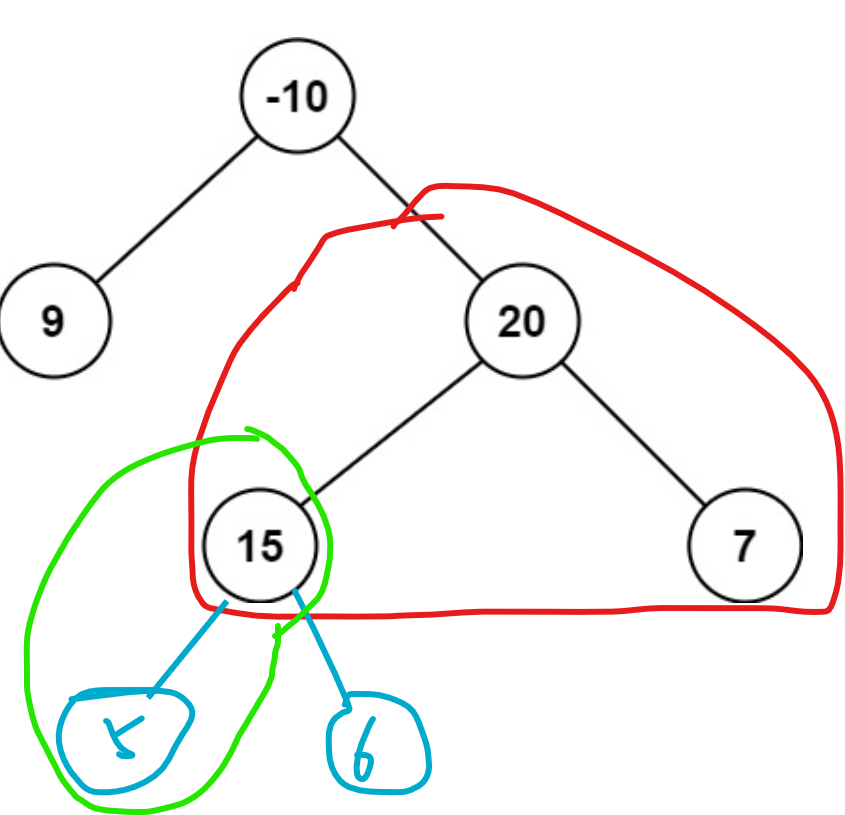
思路：考虑 dfs，因为是二叉树，所以我每个点最多走一遍，正常来说时间复杂度是满足的，然后我们将最上面我们要取的点称作答案顶点，就比如下图中的 “20” 这个点，也就是说我们的全局变量 ans 会从这个顶点开始的路径中得到，那么对于每个答案顶点，我们的ans 一定是这个答案顶点的 val + 左子树和右子树的值，那么如果左子树或者右子树有负数，那答案不就错了吗？很简单，我们直接让左右子树的最大值永远大于0即可。

那么对于非答案顶点来说呢？因为每个点我只能走一遍，所以这个非答案顶点的点所能做出的贡献最大只能是自身的val加上他左右子树其中之一的最大的最大值，就比如这个 “15” 就是非答案顶点，那么它只能在 5 或 6 中选一个最大值，并加上自身的 val 再返回。

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {private int ans = Integer.MIN_VALUE;public int maxPathSum(TreeNode root){dfs(root);return ans;}public int dfs(TreeNode node){if(node == null) return 0;int leftMaxn = Math.max(dfs(node.left), 0);int rightMaxn = Math.max(dfs(node.right), 0);int tmp = node.val + leftMaxn + rightMaxn;ans = Math.max(ans, tmp);return node.val + Math.max(leftMaxn, rightMaxn);}/**题目读错了 太 2B 了 ! ! !*/
}

7：322. 零钱兑换 - 力扣（LeetCode）

题意：给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数amount，表示总金额。

计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。你可以认为每种硬币的数量是无限的

思路：完全背包问题的板子题，注意完全背包和01背包的区别就是，完全背包在对于容量那一层循环进行遍历的时候是正着遍历，而01背包是倒着遍历，原因就是完全背包的每个物品可以用无数次

class Solution {public int coinChange(int[] coins, int amount) {int[] dp = new int[amount + 2];Arrays.fill(dp, 10005);dp[0] = 0;int n = coins.length;for(int i = 0 ; i < n; i ++){for(int j = coins[i]; j <= amount; j ++){dp[j] = Math.min(dp[j - coins[i]] + 1, dp[j]);}}if(dp[amount] == 10005) return -1;else return dp[amount];}
}

8：494. 目标和 - 力扣（LeetCode）

题意：给定一个非负的整数数组，和一个目标值 tar，然后你可以在每个元素前面设置 "+" 或者 “-”

，然后把这些元素全部加起来，有几种方法可以凑成 tar;

思路：很简单的爆搜模板题

class Solution {private int ans = 0;public int findTargetSumWays(int[] nums, int target) {int n = nums.length;dfs(0, n, 0, target, nums);return ans;}public void dfs(int cnt, int n, int sum, int target, int[] nums){if(cnt == n){if(sum == target) ans ++;return;}dfs(cnt + 1, n, sum + nums[cnt], target, nums);dfs(cnt + 1, n, sum - nums[cnt], target, nums);}
}

9：461. 汉明距离 - 力扣（LeetCode）

题意：两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目，给你两个整数 x 和 y，计算并返回它们之间的汉明距离

思路：直接异或两个数，然后把异或后的这个数当成二进制来看，里面有几个1距离就是几

class Solution {public int hammingDistance(int x, int y) {int ans = 0;int tar = x ^ y;while(tar > 0){int tmp = tar % 2;tar /= 2;if(tmp == 1) ans ++;}return ans;}
}

10：448. 找到所有数组中消失的数字 - 力扣（LeetCode）

题意：给你一个含 n 个整数的数组 nums ，其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出现在 nums 中的数字，并以数组的形式返回结果

思路：我这里是用双指针慢慢找的，写的比较屎山代码，官方的代码比较简单，也很好懂，就是把nums 当成哈希表存，最后遍历一遍 nums 就可以了

class Solution {public List<Integer> findDisappearedNumbers(int[] nums) {int n = nums.length;Arrays.sort(nums);List<Integer> ans = new ArrayList<>();int st = 1;int ed = nums[0];for(int k = st; k < ed; k ++) ans.add(k);for(int i = 0; i < n; i ++){for(int j = i + 1; j < n; j ++){if(nums[j] != nums[i]){if(nums[j] != nums[i] + 1){st = nums[i];ed = nums[j];for(int k = st + 1; k < ed; k ++) ans.add(k);}if(j == n - 1){st = nums[j];ed = n;for(int k = st + 1; k <= ed; k ++) ans.add(k);}i = j - 1;break;}if(j == n - 1){st = nums[i];ed = n;for(int k = st + 1; k <= ed; k ++) ans.add(k);i = j;break;}}}return ans;}
}

class Solution {public List<Integer> findDisappearedNumbers(int[] nums) {int n = nums.length;for (int num : nums) {int x = (num - 1) % n;if (nums[x] <= n) {nums[x] += n;}}List<Integer> ret = new ArrayList<Integer>();for (int i = 0; i < n; i++) {if (nums[i] <= n) {ret.add(i + 1);}}return ret;}
}作者：力扣官方题解
链接：https://leetcode.cn/problems/find-all-numbers-disappeared-in-an-array/solutions/601946/zhao-dao-suo-you-shu-zu-zhong-xiao-shi-d-mabl/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。