关于熵减 - 飘升机
考虑非对称电容,
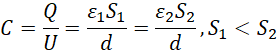
保持真空磁导率不变(变化的情况不在这里讨论),
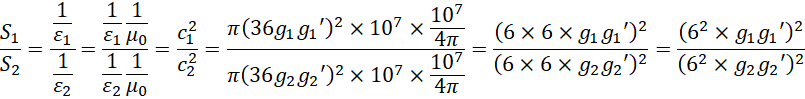
抽象出关系,
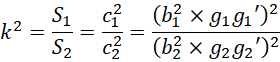
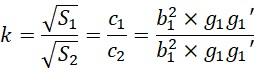
![]()
其中![]() 和
和![]() 都有两种模式,
都有两种模式,
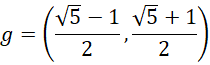
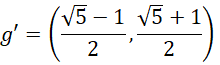
同时要求,
![]()
因为都是质数,
![]()
各自构成光速的两个质数的关系,体现于选取的![]() 组合的4种模式之一:
组合的4种模式之一:
![]() 连续提升,
连续提升,![]() 连续下降,
连续下降,![]() 保持平衡,
保持平衡,![]() 反向保持平衡。
反向保持平衡。
在![]() 模式选定之后,互相的关系体现为,
模式选定之后,互相的关系体现为,
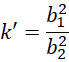
![]()
![]()
![]()
比率![]() 越接近于0,两极板之间由于绝对速度构成的差异体现出来的力越明显。产生这种力是因为,
越接近于0,两极板之间由于绝对速度构成的差异体现出来的力越明显。产生这种力是因为,
![]()
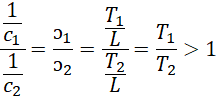
也就是小极板一侧对空间产生的影响使得空间的频率相对于大极板一侧下降,周期延长,进而导致设备向着小极板一侧滑落。从原理上来说,这个力其实就是引力的一种表现形式。可见,在长度单位被认为是一样的前提下,数值越小的光速,周期越长,频率越低。但这种低频率导致了向着它的方向出现引力效应。
考虑已知,
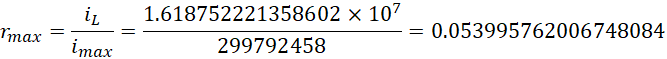
我们知道电子的内在电压是0.511MV,它乘以这个比率,
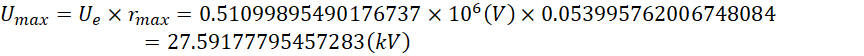
也就是说,只要提供![]() 的电压,就可以模拟一个电子的内部频率变化,可以在宏观尺度准备出电子内部的频率变化环境,进而建立一个大号的电子。
的电压,就可以模拟一个电子的内部频率变化,可以在宏观尺度准备出电子内部的频率变化环境,进而建立一个大号的电子。
如果使用平衡前提下的光速数值,
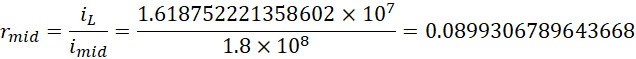
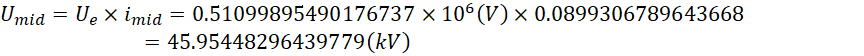
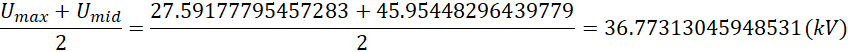
考虑两个极板的情况,正极板尽可能的高频,负极板尽量保持中性,则应当取平均电压,![]() ,才能仅产生升力而不产生频率提升的效果。负极板尽可能的大就倾向于保证这一点。
,才能仅产生升力而不产生频率提升的效果。负极板尽可能的大就倾向于保证这一点。
我们知道,飘升机的两个极板,面积小的极板为正极,面积大的极板为负极的时候产生的升力更大,这是因为正电荷产生的中心频率高,导致周围空间的频率更低。无论正负电荷,频率的分布如下图所示,现 在,让我们根据上面获得的认识,构造一个非对称电容飘升机。
先给出阿伏伽德罗常数,
![]()
根据定义,1mol碳12原子具有![]() 个原子,其质量为12克。
个原子,其质量为12克。
铜元素相对原子质量为63.546。1mol铜原子的质量为63.546g,1kg铜原子的个数为,
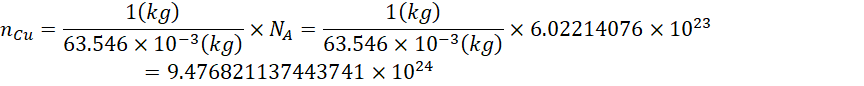
铜元素具有2个价电子,1kg铜原子的总价电子数为,
![]()
铁元素相对原子质量为55.85,1mol铁原子的质量为55.85g,1kg铁原子的个数为,
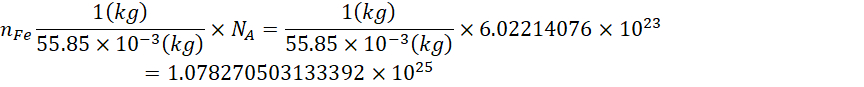
铁元素具有2个价电子,1kg铁原子的总价电子数为,
![]()
为了让铜和铁构成的极板电子数匹配,我们需要的质量比为,
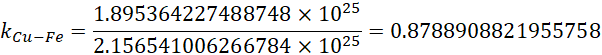
因为力的本质就是频差,且已知,
![]()
单个电子的内在频差为,
![]()
所以单个电子可以提供,
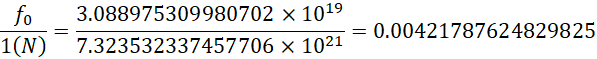
f0=0.00421787624829825(N)![]()
因为电子和正电子的频率中心的差距就是单个电子的内部频差,所以正负电子对的单向频差也是这个数值,而这个频差对应的力约为千分之四点二牛顿。用![]() 铜和
铜和![]() 铁构成的两个极板,具有
铁构成的两个极板,具有![]() 个电子对,可产生的力可以积累为,
个电子对,可产生的力可以积累为,
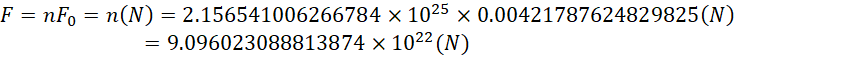
这是一个极其巨大的力:这是和事实不相符的。实际上的非对称电容不会用这么多的铜和铁来作为极板的有效面积。还有就是,这个力是极板之间的内力,在正负电荷分开之后,正电荷和负电荷的频差,被负电荷和正电荷的反向频差抵消了,所以不会向着外界输出力的效果。所以才要用非对称电容打破这个平衡而产生单向力。
电子内在频差为![]() 对应于内在电压为,
对应于内在电压为,
![]()
我们现在既然把电子拉开为电子对,极板之间的电压也会影响![]() 的实际值,
的实际值,
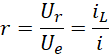
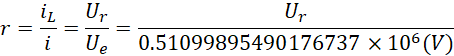
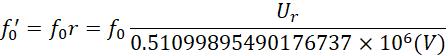
![]() 和
和![]() 比率确定
比率确定![]() 和
和![]() 的大小。此时双向力公式修正为,
的大小。此时双向力公式修正为,
![]()
让这个力提起一定质量的重物,假定提起的质量为m,
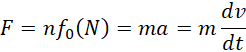
回忆先前的引力加速度,
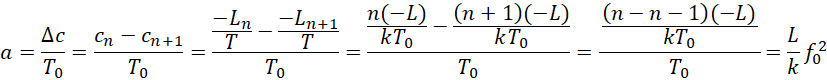
写出对应的形式,
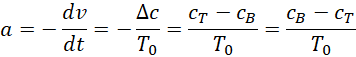
配合虚数单位的比率,
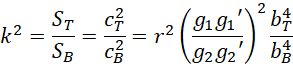
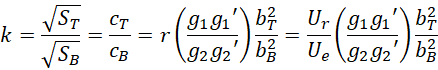
令,
![]()
导出加速度为,
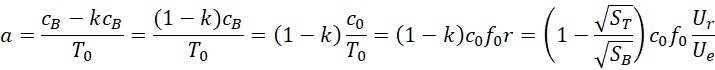
因为这个加速度是由空间频差造成的,所以它可以作用于其中的任何质量而不受质量大小的限制。回到,
![]()
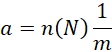
对比,
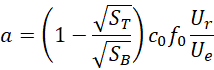
合并,
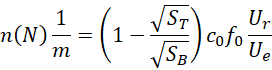
可见这个系统的力产生加速度的方式,
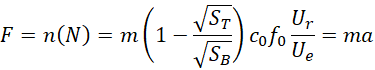
单个电子对产生的加速度,完全由两个极板的面积的平方根比和外加电压与电子内在电压的比的乘积决定,
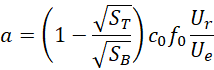
而无论其中加载的质量有多大,所以,本质上来说,这就是一种引力效应。多个电子对产生的累积加速度和使用的材料的价电子个数,材料的质量以及阿伏伽德罗常数有关,如果使用两种材料,选择质量比上相对原子质量的比值较小的即可,
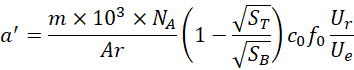
其中![]() 为相对原子质量。我们看到虽然无论如何,
为相对原子质量。我们看到虽然无论如何,
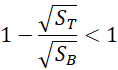
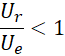
但是![]() 的数值极大,
的数值极大,
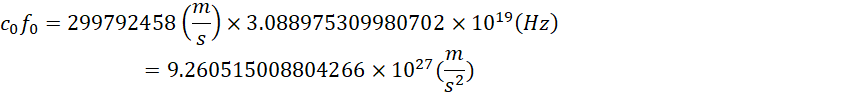
即便是考虑阿伏伽德罗常数所导致的加速度分配,
![]()
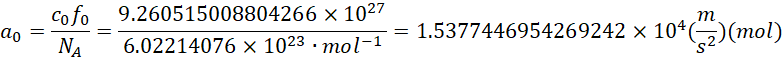
![]()
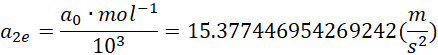
单个价电子对,每千分之一摩尔的平均加速度仍然可以达到15.3774个单位加速度。而重力加速度只有9.8个单位加速度。所以通过调节极板的面积比率以及输入的电压Ur![]() 完全可以实现在地面上的反重力托举行为(高电压可能造成危险需要考虑)。
完全可以实现在地面上的反重力托举行为(高电压可能造成危险需要考虑)。
一摩尔的意义是12克碳12具有的原子数量,也就是1克氢原子具有的氢原子数量,一摩尔的一千分之一就是一千克氢原子具有的氢原子数量。一对电子可以造成的频差(或者时间差)被平分到一千克氢原子上,每个氢原子仍然可以获得15.377个单位加速度,而地球给出的万有引力,则是每个氢原子(其实可以是任何东西)都只能获得9.8个单位加速度。所以如果是氢原子提供一个电子,那么这一个电子拉升一千克的氢原子脱离地面都绰绰有余。虽然铜和铁等金属元素的原子只有少数几个可用的价电子,但是我们这里说的是一个原子的价电子和一千克原子的加速度的关系,而两者相差二十三个数量级,所以无论如何都有足够的空间安排两者的比例关系。
极板面积的比率修改光速的做法在于修改两组质数乘积之间的比例关系,但是这个做法仍然是十分粗糙的。主要在于单组质数中,两个质数之间的关系是不能确定的。我们需要确定两个质数之间的关系,以决定在时空中的前进还是后退提升还是下降。操作这个关系,我们就可以进入四维(前进后退),以及五维(提升下降);两个质数乘积作为结果,又把世界分成若干个平行世界,这些平行世界又可以成为维数的划分标准,所以这些维数加起来,加上无向的过程维,就可以有,
![]()
个维数。
在光速的构成上,决定时间方向和空间升降的,主要是a和b之间的排列顺序。而a和b的数值的乘积则决定了不同的平行世界。可以认为飘升机可以临时改变ab的乘积,但不能改变ab的排列顺序,也就是说可以临时沟通平行世界。当然如果有能力完全该百年ab的乘积,则可以在不同的平行世界之间无缝切换。由于质数的数量是无限多的,两个质数的乘积也是无限多的,平行世界的个数是无限多的。两个质数之间的前后排列则决定了那个平行世界的时间方向。先后两对质数乘积(也就是q)的排列方式则决定了那个世界是膨胀还是收缩。
回到飘升机的设计,输入的电压有可能临时改变真空介电常数的数值,也就是改变,
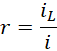
也有可能永久性的改变这个数值,因为它可能会影响到,
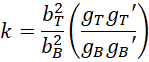
其中的q和g,进而导致材料的永久性改变。而输入的电压不应该改变材料的特质,之应当改变空间的特质。由此来说,对于输入电压应当给以调制,比如输入电压的频率应当尽可能的避免改变材料本身。考虑到高频输入具有趋肤效应,可能应当对两极接入高频脉冲高压。为什么不输入正弦波形式的电压?因为这导致小极板构成天线,或者出现能量交换。
飘升机能够对质量提供加速度,是因为它构造了空间密度的梯度场。物体被这个梯度场牵引,那么这个牵引的力是否做功?因为如果做功通常就意味着有能量的转换,比如动能或者电能转换为重力势能。
常规场做功,用的是,
![]()
也就是力施加于特定的质量,而做功则意味着在力的方向上发生位移,
![]()
非对称电容只产生加速度场,
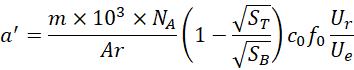
它就像是重力产生的重力场,
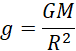
如果认为重力做功,那么是什么能量转换为重力做功的能量。我们知道,并没有任何能量转化为重力做功的能量,也就是说,重力做功并不涉及其它能量的转化,而是物体的重力势能被转化为动能,或者动能转化为重力势能。我们用相同的方法创造的类重力场,显然也是不涉及其它能量转化为类重力场的能量的。但无论如何,我们需要维持这个类重力场的存在,可能需要维持一个微小的电流以抵消微小漏电。所以非对称电容系统,若封闭良好,其中气体绝缘性好,几乎不漏电,它基本上是无需消耗其它能量比如电能的。而且它完全可以自己托举自己,具有自举的能力。
