【LeetCode】363. 矩形区域不超过 K 的最大数值和 (二分 + 前缀和)

363. 矩形区域不超过 K 的最大数值和 - 力扣（LeetCode）

题目：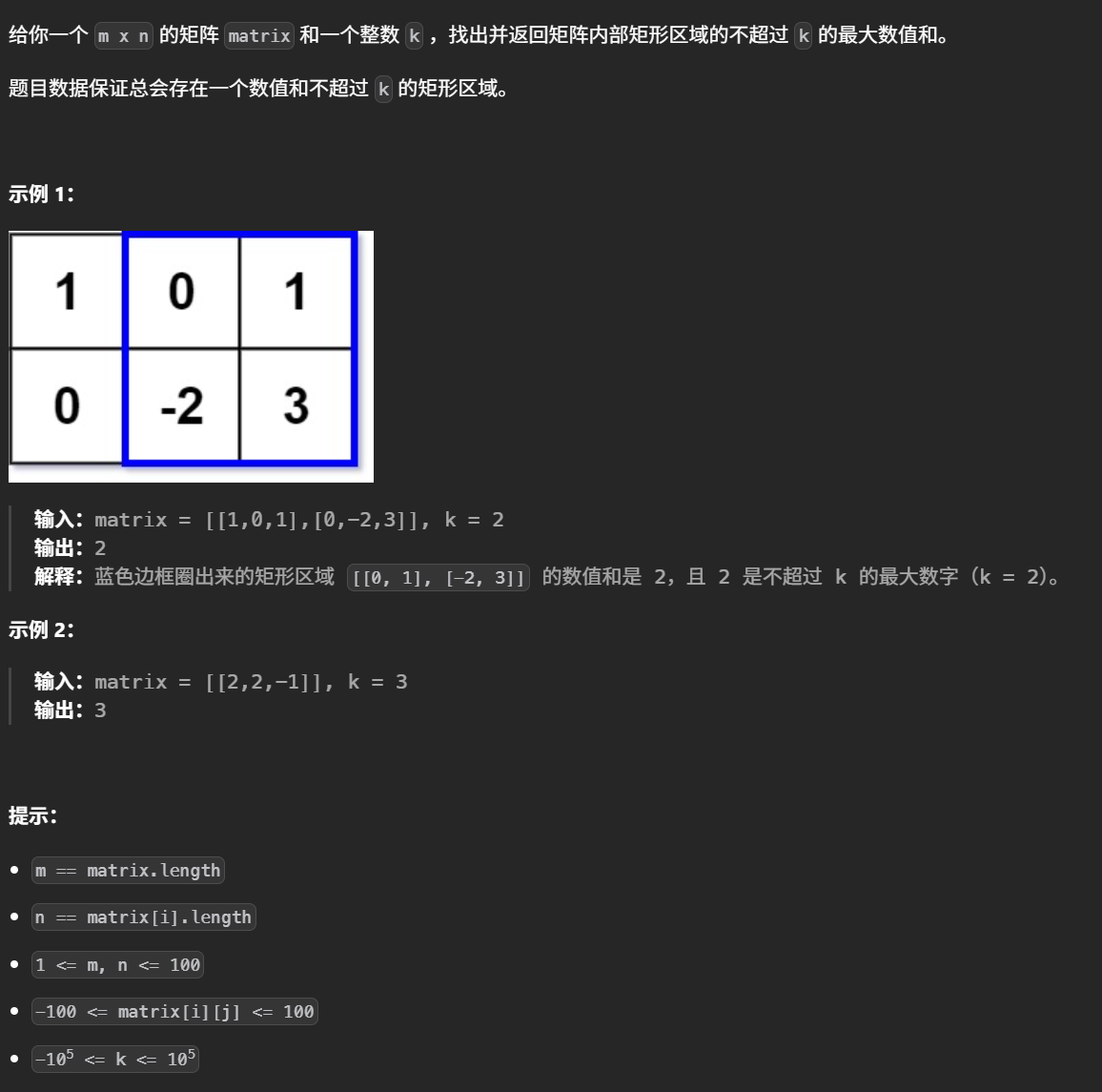

思路：

面对这种计算矩形的题目，我们可以考虑枚举矩形的上下边界，然后依次遍历列来进行计算，这样能从 n²m² 优化至 n²m

本题让我们求满足矩形和 sum <= k 的最大 sum，那么如果直接暴力枚举矩形的端点显然是不行的，考虑优化

我们枚举矩形的上下边界，同时使用一个前缀和来储存矩形前 i 列的和，那么这样题目就相当于变成了：给你一个数组，让你求一个连续段不超过 k 的最大 sum

考虑当前第 z 列的前缀和 s，如果我们要让其和最大，那么之前的端点就要满足 sum[z] - sum[l] = k 即 sum[l] = sum[z] - k = s - k

如果暴力查找显然是会超时的，所以不妨考虑二分，我二分出第一个大于等于 s-k 的 sum[l]，然后计算即可

具体实现看代码，很简单，特别注意初始化 ans 为负无穷大，因为矩阵的和能是负数

代码：

class Solution {
public:int maxSumSubmatrix(vector<vector<int>>& matrix, int k) {int ans = -1e9;int n = matrix.size();int m = matrix[0].size();for(int i = 0;i < n;i++){vector<int> sum(m,0);for(int j = i;j < n;j++){for(int z = 0;z < m;z++){sum[z] += matrix[j][z];}set<int> st;st.insert(0);int s = 0;for(auto & x : sum){s+=x;auto l = st.lower_bound(s-k);if(l != st.end()) ans = max(ans,s - *l);st.insert(s);}}}return ans;}
};