CF每日4题(1500-1700)

经验+4

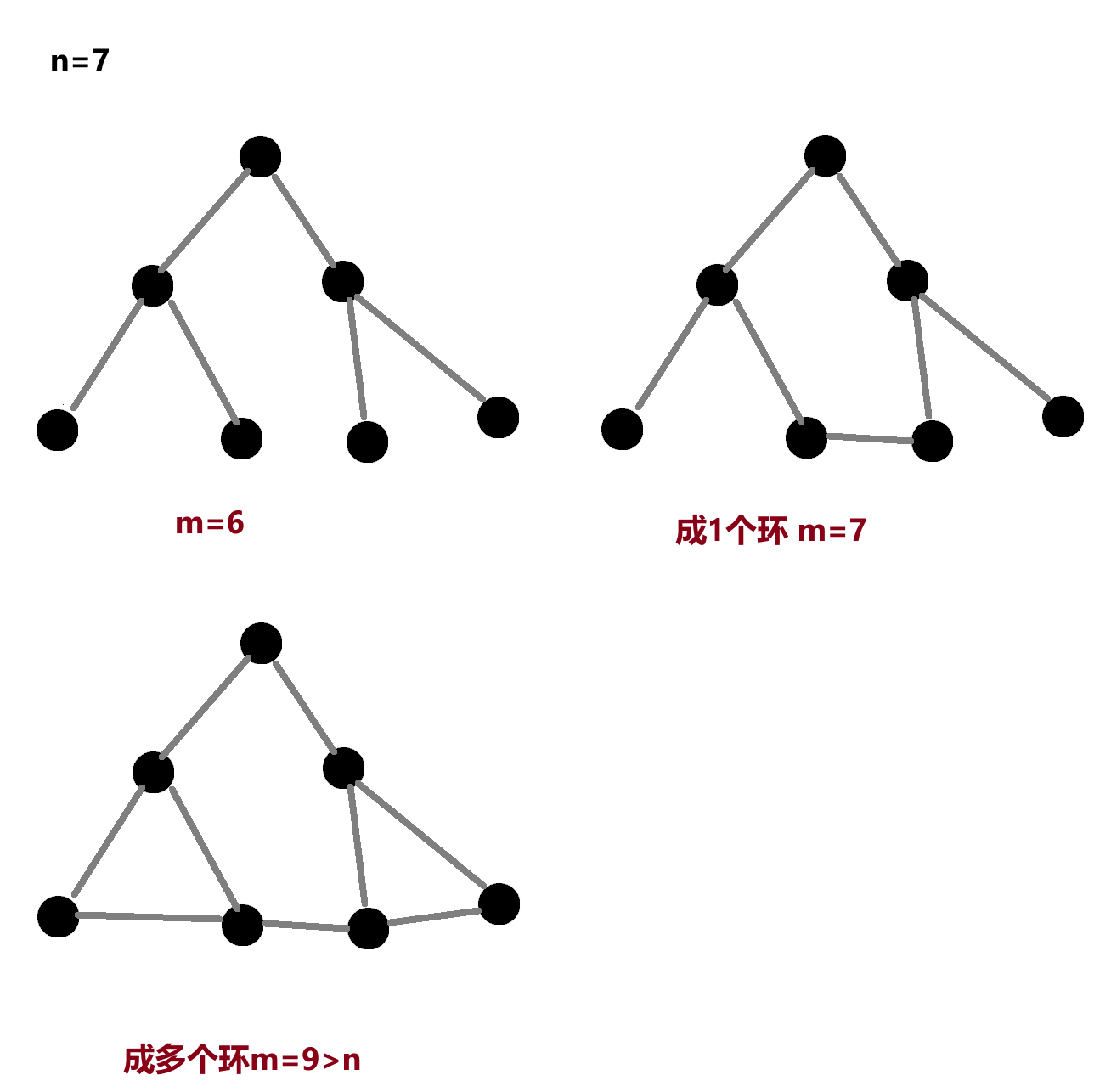
• 103B 克苏鲁可爱捏+发现图点和边的数量规律
• 1198A 滑动窗口
• 255C 二维dp求最小值
• 1496C $a_x=\lceil \frac{a_x}{a_y}\rceil$，用\sqrt{}​优化次数

103B 图 并查集1500

const int N=1e6+10,mod=1e9+7,inf=1e9+10;
int fa[N];
int findf(int x){if(fa[x]==x)return x;return fa[x]=findf(fa[x]);
}
void merge(int x,int y){int fx=findf(x),fy=findf(y);if(fx==fy)return;fa[fy]=fa[fx];
}
void solve(){int n,m;cin>>n>>m;forr(i,1,n)fa[i]=i;forr(i,1,m){int u,v;cin>>u>>v;merge(u,v);}if(n==m){//使用并查集确认是不是只有一个连通块int fg=0;forr(i,1,n)fg+=(fa[i]==i);cout<<(fg==1?"FHTAGN!":"NO")<<endl;}else cout<<"NO"<<endl;
}

1198A 滑动窗口 1600

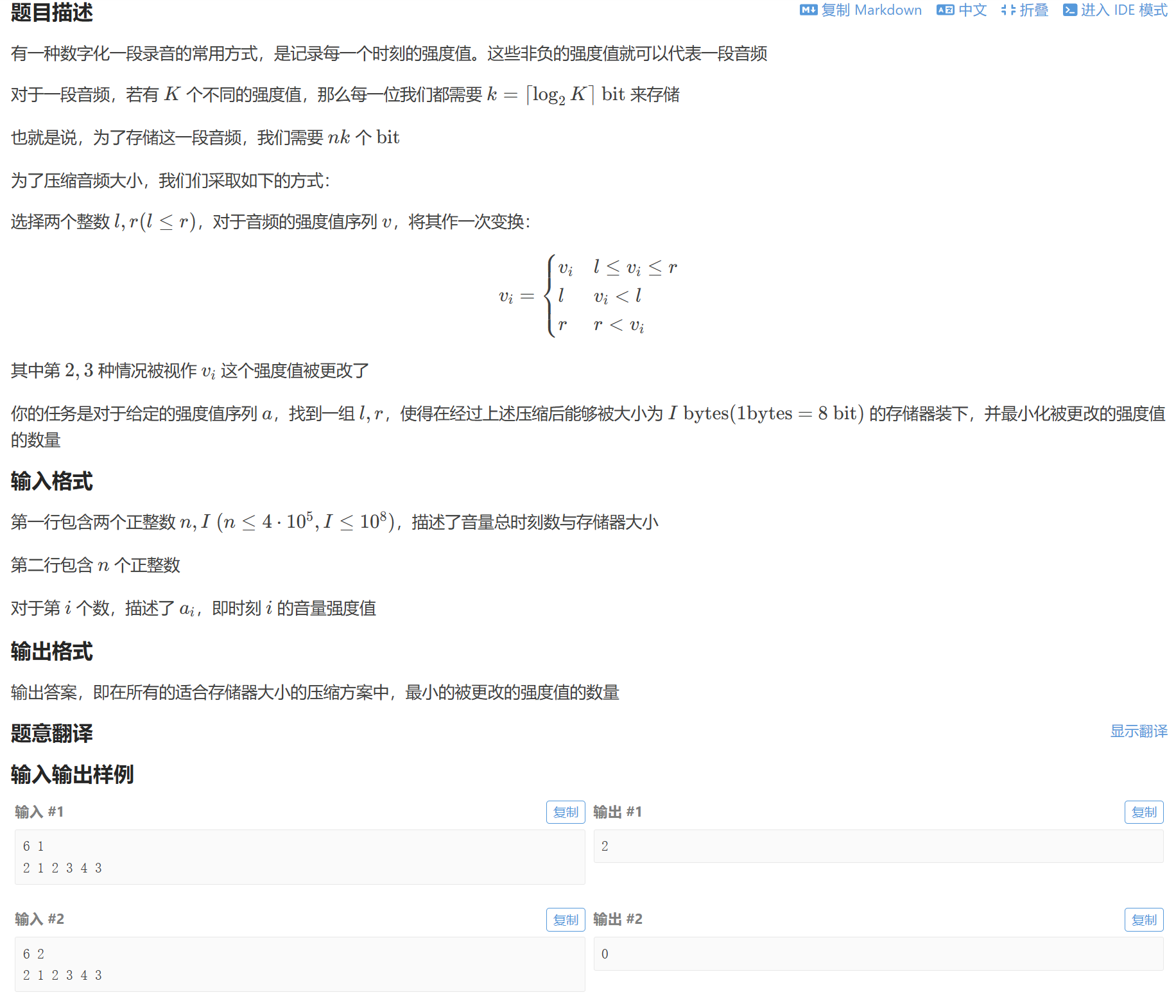
题意：改变最少的数，让数组中的不同数值数为给定值
注意留下的数应该大小上是连续的，因为强度值要在$[l,r]$范围内
所以采用滑动窗口

map<int,int>mp;
set<int>s;
void solve(){int n,m;cin>>n>>m;vector<int>a(n+1);forr(i,1,n){cin>>a[i];mp[a[i]]++;s.insert(a[i]);}int k=8*m/n;if(k>=31)return cout<<0<<endl,void();//2^k>4e5 溢出输出0k=(1<<k);//最大种数if(k>=s.size())return cout<<0<<endl,void();//可以容下全部数 不用改//滑动窗口int ans=0,sm=0;auto l=s.begin(),r=s.begin();forr(i,1,k){sm+=mp[*r];r++;}while (r!=s.end()){sm=sm-mp[*l]+mp[*r];l++,r++;ans=max(sm,ans);}cout<<n-ans<<endl;
}

225C dp 1700

//从前向后 收集型
//从i-1更新i i可以变色，或延续不变色
string s[N];
int cnt[N][2],dp[N][N][2];//第i列 宽度j 颜色c
void solve(){int n,m,x,y;cin>>n>>m>>x>>y;memset(dp,0x3f,sizeof dp);//要求最小值，注意初始化为infforr(i,1,n){cin>>s[i];s[i]=' '+s[i];}forr(i,1,m){forr(j,1,n){cnt[i][0]+=(s[j][i]=='.');cnt[i][1]+=(s[j][i]=='#');}}dp[1][1][0]=cnt[1][0],dp[1][1][1]=cnt[1][1];//第一个不用看前面的状态forr(i,2,m){forr(c,0,1){forr(j,x,y){//变色dp[i][1][c]=min(dp[i-1][j][c^1]+cnt[i][c],dp[i][1][c]);}forr(j,2,y){//不变色dp[i][j][c]=dp[i-1][j-1][c]+cnt[i][c];}}}int ans=0x3f3f3f3f;forr(j,x,y){ans=min({dp[m][j][0],dp[m][j][1],ans});}cout<<ans<<endl;
}

另有dalao前面更新后面的思路

1469C 思维 数学 1700

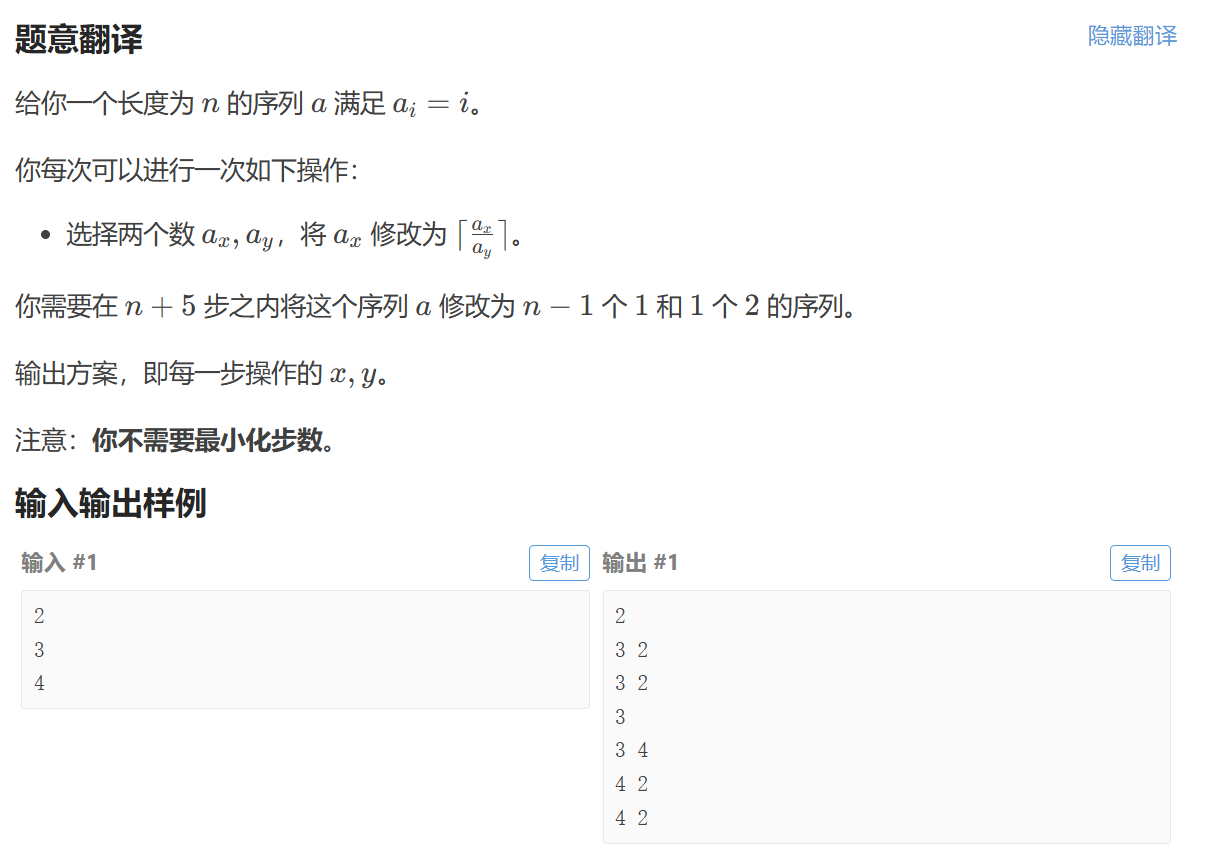
有点红温，死磕log的处理方法，但是$lo{g}_{2}2e5>17$，一直想着怎么优化才好，没换个思路。
看题解发现利用$\sqrt{n}$就好，2e5五层\sqrt{}​就到1了

• $\lceil \frac{i}{i+1}\rceil =1$
• $\sqrt{n}$和$n$之间的数选$y=n$就可以
• $n=\sqrt{n}\sqrt{n}$，多操作一下，n就能变1
• $\sqrt{n}$由$\sqrt{\sqrt{n}}$两次解决

struct pr
{int x,y;
};
void solve(){int n;cin>>n;vector<pr>ans;while (n>2){int q=ceil(sqrt(n));forr(i,q+1,n-1)ans.push_back({i,i+1});ans.push_back({n,q});ans.push_back({n,q});n=q;}cout<<ans.size()<<endl;for(auto i:ans){cout<<i.x<<' '<<i.y<<endl;}
}