DAG的DP(UVA437 巴比伦塔 The Tower of Babylon)
DAG 上的 DP 知识点
DAG 的基本概念
DAG 是一种没有环路的有向图,具有拓扑序特性。动态规划在 DAG 上的应用通常基于拓扑序或记忆化搜索。(像我这种暂时还没学过拓扑排序的可以用dfs+记忆化搜索)
DAG 上 DP 的核心思想
- 状态定义:将问题抽象为 DAG 上的节点,状态转移对应图中的边。
- 状态转移:根据拓扑序或记忆化搜索,逐步更新状态值。
- 初始化:明确边界条件(如起点或终点的状态值)。
常见问题类型
- 最长路径问题:求解 DAG 中从起点到终点的最长路径。
- 最短路径问题:求解 DAG 中从起点到终点的最短路径。
- 依赖关系问题:如任务调度、课程安排等具有依赖关系的场景。
实现方法
方法 1:记忆化搜索
通过递归和缓存中间结果实现 DP。
#include <vector>
#include <cstring>
using namespace std;const int N = 1000;
vector<int> adj[N];
int memo[N];int dfs(int u) {if (memo[u] != -1) return memo[u];int res = 0;for (int v : adj[u]) {res = max(res, dfs(v) + 1);}return memo[u] = res;
}void dag_dp(int n) {memset(memo, -1, sizeof(memo));for (int i = 0; i < n; ++i) {if (memo[i] == -1) dfs(i);}
}
方法 2:拓扑排序 + DP
- 拓扑排序:使用 Kahn 算法或 DFS 生成拓扑序。
- DP 更新:按拓扑序依次更新每个节点的状态值。
#include <vector>
#include <queue>
using namespace std;const int N = 1000;
vector<int> adj[N]; // 邻接表
int in_degree[N]; // 入度数组
int dp[N]; // DP 数组void dag_dp(int n) {queue<int> q;for (int i = 0; i < n; ++i) {if (in_degree[i] == 0) {q.push(i);dp[i] = 0; // 初始化起点状态}}while (!q.empty()) {int u = q.front();q.pop();for (int v : adj[u]) {dp[v] = max(dp[v], dp[u] + 1); // 状态转移if (--in_degree[v] == 0) {q.push(v);}}}
}
注意事项
- 拓扑序的正确性:确保 DAG 的拓扑序生成无误。
- 初始状态:明确起点或终点的初始化条件。
- 状态转移方程:根据问题设计合理的转移逻辑。
UVA437 巴比伦塔 The Tower of Babylon
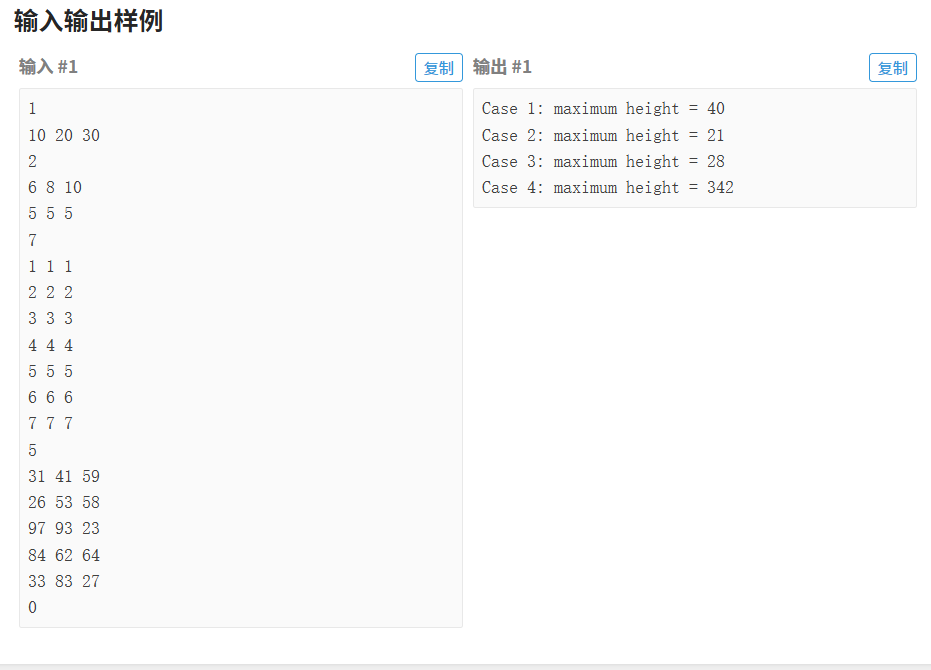
思路:
dfs+记忆化搜索
解题思路
-
数据预处理
- 每个箱子的长、宽、高被读取并存储在数组
x[]、y[]、z[]中。 - 通过交换操作确保每个箱子的三个维度按升序排列,即
x[i] ≤ y[i] ≤ z[i],这样便于后续处理。
- 每个箱子的长、宽、高被读取并存储在数组
-
动态规划定义
dp[i][w]表示以第i个箱子的第w种摆放方式作为顶部时的最大高度。w的取值(0、1、2)对应箱子的不同摆放方式:w=0:以x[i]为高度,底面为y[i] × z[i]。w=1:以y[i]为高度,底面为x[i] × z[i]。w=2:以z[i]为高度,底面为x[i] × y[i]。
-
递归函数
dfs- 记忆化搜索实现动态规划,避免重复计算。
- 对于当前箱子
i的摆放方式w,遍历所有其他箱子j的每种摆放方式k,检查是否可以将j放在i的下方。 - 如果满足条件,更新
dp[i][w]为当前值与dfs(j, k)中的较大值。
-
边界条件
- 如果
dp[i][w]已被计算过,直接返回其值。 - 最终,
dp[i][w]加上当前摆放方式的高度(x[i]、y[i]或z[i])。
- 如果
-
主函数逻辑
- 循环处理多个测试用例,直到输入
n=0时结束。 - 对每个测试用例,初始化
dp数组为0,然后遍历所有箱子的每种摆放方式,调用dfs计算最大高度。 - 输出每个测试用例的最大高度。
- 循环处理多个测试用例,直到输入
关键函数说明
-
panduan(i, w, j, k)
检查箱子j的摆放方式k是否可以放在箱子i的摆放方式w下方。具体逻辑是检查j的底面长和宽是否严格小于i的底面长和宽。 -
dfs(i, w)
递归计算以箱子i的摆放方式w作为顶部时的最大高度。通过记忆化避免重复计算,确保时间复杂度为O(n²)。
复杂度分析
- 时间复杂度:O(n²),每个箱子最多被处理3次(对应3种摆放方式),每次处理需要遍历其他所有箱子的3种摆放方式。
- 空间复杂度:O(n),
dp数组的大小为n × 3。
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<iostream>
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int n;
int x[35], y[35], z[35];
int dp[100][3];
bool panduan(int i, int w, int j, int k) {int l, r, u, v;l = (w == 0 ? y[i] : x[i]);r = (w == 2 ? y[i] : z[i]);u = (k == 0 ? y[j] : x[j]);v = (k == 2 ? y[j] : z[j]);if (u < l && v < r) {return true;}else {return false;}
}
int dfs(int i, int w) {if (dp[i][w] != 0) {return dp[i][w];}for (int j = 0; j < n; j++) {for (int k = 0; k <= 2; k++) {if (panduan(i, w, j, k)) {dp[i][w] = max(dp[i][w], dfs(j, k));}}}if (w == 0) {dp[i][w] += x[i];}else if (w == 1) {dp[i][w] += y[i];}else {dp[i][w] += z[i];}return dp[i][w];
}
int main(){ios::sync_with_stdio(false); // 禁用同步cin.tie(nullptr); // 解除cin与cout绑定int ans = 0;while (true) {ans++;cin >> n;if (n == 0) {return 0;}for (int i = 0; i < n; i++) {cin >> x[i] >> y[i] >> z[i];if (x[i] > y[i]) {swap(x[i], y[i]);}if (x[i] > z[i]) {swap(x[i], z[i]);}if (y[i] > z[i]) {swap(y[i], z[i]);}}memset(dp, 0, sizeof(dp));int r = 0;for (int i = 0; i < n; i++) {r = max(r, dfs(i, 0));r = max(r, dfs(i, 1));r = max(r, dfs(i, 2));}cout << "Case " << ans << ": maximum height = " << r << endl;}return 0;
}
