最小生成树的普利姆算法和克鲁斯卡尔算法

最小生成树的概念：指含有图中全部顶点的极小连通子树，包含所有顶点n，但只有足以构成一棵树的n-1条边

求最小生成树可以采用普利姆算法和克鲁斯卡尔算法
以下图为例

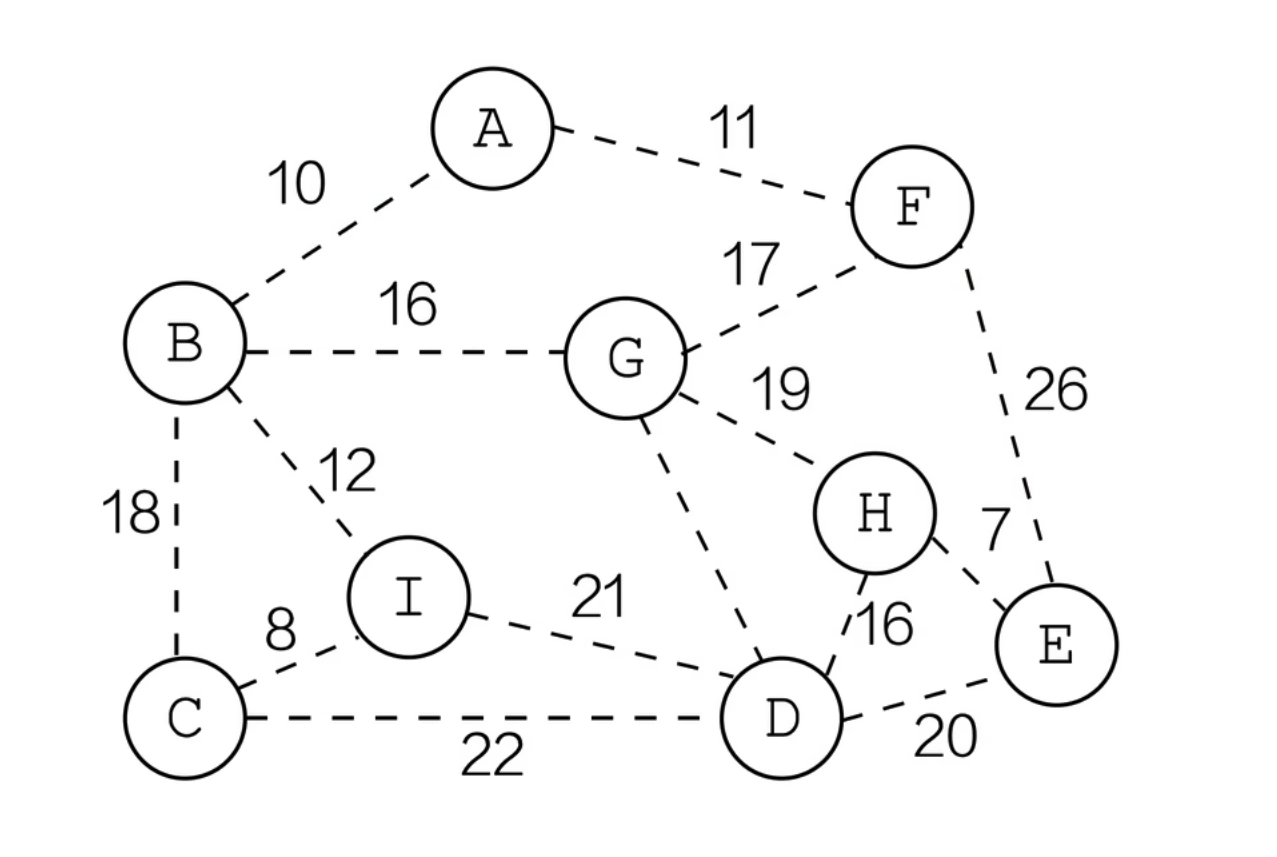
先构造带权图

#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 100
#define MAX 0x7fffffff
typedef char VertexType;
typedef int EdgeType;
typedef struct
{//顶点数组VertexType vertex[MAXSIZE];//边的二维数组EdgeType arc[MAXSIZE][MAXSIZE];int Vertex_num;int Edge_num;
}Mat_graph;
int visit[MAXSIZE];
//构建带权图
void creat_graph(Mat_graph* G)
{G->Vertex_num = 9;G->Edge_num = 15;G->vertex[0] = 'A';G->vertex[1] = 'B';G->vertex[2] = 'C';G->vertex[3] = 'D';G->vertex[4] = 'E';G->vertex[5] = 'F';G->vertex[6] = 'G';G->vertex[7] = 'H';G->vertex[8] = 'I';for (int i = 0;i < G->Vertex_num;i++){for (int j = 0;j < G->Vertex_num;j++){if (i == j){G->arc[i][j] = 0;}else{G->arc[i][j] = MAX;}}}G->arc[0][1] = 10;G->arc[0][5] = 11;G->arc[1][2] = 18;G->arc[1][6] = 16;G->arc[1][8] = 12;G->arc[2][3] = 22;G->arc[2][8] = 8;G->arc[3][4] = 20;G->arc[3][6] = 24;G->arc[3][7] = 16;G->arc[3][8] = 21;G->arc[4][5] = 26;G->arc[4][7] = 7;G->arc[5][6] = 17;G->arc[6][7] = 19;for (int i = 0;i < G->Vertex_num;i++){for (int j = 0;j < G->Vertex_num;j++){G->arc[j][i] = G->arc[i][j];}}
}

普利姆算法
普利姆算法：从一个顶点开始，每次比较待选的所有路径，并选择最小的路径，直到每个顶点都遍历一遍
代码实现

//普利姆算法
void  prim(Mat_graph* G)
{int i, j, k;int min;//待比较的权值int weight[MAXSIZE];//记录边，数组中的值表示出发点，数组下标表示到达点int index[MAXSIZE];for (i = 0;i < G->Vertex_num;i++){weight[i] = G->arc[0][i];index[i] = 0;}for (int i = 1;i < G->Vertex_num;i++){min = MAX;j = 0;k = 0;while (j < G->Vertex_num){if (weight[j] != 0 && weight[j] < min){min = weight[j];k = j;}j++;}printf("(%c,%c)\n", G->vertex[index[k]], G->vertex[k]);weight[k] = 0;//比较新的结点的权值，并把边记录下去for (int j = 0;j < G->Vertex_num;j++){if (weight[j] != 0 && G->arc[k][j] < weight[j]){weight[j] = G->arc[k][j];index[j] = k;}}}
}

主函数

int main()
{Mat_graph G;creat_graph(&G);prim(&G);printf("\n");return 0;
}

克鲁斯卡尔算法
克鲁斯卡尔算法是对边进行操作，先找权值最小的边，在依次选择，但要注意避免形成回路
代码如下
其中构造带权图的代码和上面一样

#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 100
#define MAX 0x7fffffff
typedef char VertexType;
typedef int EdgeType;
typedef struct
{//顶点数组VertexType vertex[MAXSIZE];//边的二维数组EdgeType arc[MAXSIZE][MAXSIZE];int Vertex_num;int Edge_num;
}Mat_graph;
//边的存储
typedef struct
{int begine;int end;int weight;
}Edge;
//交换
void swap(Edge* a, Edge* b)
{Edge temp;temp = *a;*a = *b;*b = temp;
}
//将边数组从小到大进行排序
void sortEdge(Edge edgh[], int edge_num)
{for (int i = 0;i < edge_num;i++){for (int j = i + 1;j < edge_num;j++){if (edgh[i].weight > edgh[j].weight){swap(&edgh[i], &edgh[j]);}}}
}
//避免形成回路
int find(int* parent, int index)
{while (parent[index] > 0){index = parent[index];}return index;
}
//克鲁斯卡尔算法
void Kruskal(Mat_graph* G)
{Edge edgh[MAXSIZE];int k = 0;for (int i = 0;i < G->Vertex_num;i++){for (int j = i+1;j < G->Vertex_num;j++){if (G->arc[i][j] < MAX){edgh[k].begine = i;edgh[k].end = j;edgh[k].weight = G->arc[i][j];k++;}		}}sortEdge(&edgh, G->Edge_num);int parent[MAXSIZE];for (int i = 0;i < G->Vertex_num;i++){parent[i] = 0;}int m, n;for (int i = 0;i < G->Edge_num;i++){m = find(parent, edgh[i].begine);n = find(parent, edgh[i].end);if (m != n){parent[m] = n;printf("(%c,%c) %d\n", G->vertex[edgh[i].begine], G->vertex[edgh[i].end], edgh[i].weight);}}
}

主函数

int main()
{Mat_graph G;creat_graph(&G);Kruskal(&G);printf("\n");return 0;
}

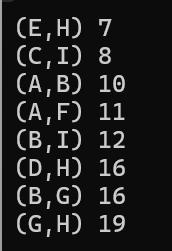
在最小生成树中，库鲁斯卡尔算法针对边进行操作，适合边数少的情况。而普里斯算法针对顶点，适用于边数多的情况