当前位置：首页 > news >正文

自然语言处理——03 RNN及其变体

news 2025/8/22 10:51:17

1 认识RNN

1.1 概念

循环神经网络 RNN （Recurrent Neural Network，简称RNN）——处理序列数据的神经网络；
- 一般以序列数据作为输入，通过网络内部的结构设计有效捕捉序列之间的关系特征，一般也是以序列形式进行输出；
- 应用场景：比如自然语言（句子是“词的序列”）、时间序列（股票价格是“时间点的序列”）、音频（声音是“波形的序列”）；
- 独特能力：普通神经网络“看一个样本是一个样本”（比如识别单张图片），但 RNN 能记住前面的信息，用历史信息辅助当前判断；
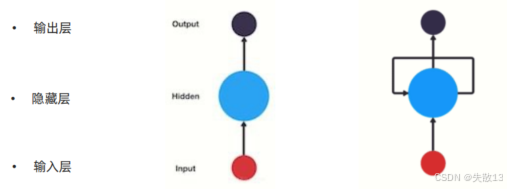
RNN网络结构：左图是普通神经网络结构，右图是RNN神经网络结构
- 输入层：接收“序列中的一个元素”（比如句子里的一个词，股票的一个时间点价格）；
- 隐藏层：RNN 的核心！负责存历史信息 ：上一个时间步（比如上一个词）的隐藏层输出，会作为当前时间步的输入，和新数据一起计算；
- 输出层：输出当前时间步的结果（比如预测下一个词，预测下一时间点价格）；
为什么叫“循环”？——因为隐藏层自己连接自己
- 普通神经网络：隐藏层输出直接给输出层；
- RNN 隐藏层：上一个时间步的输出会在下一个时间步作为输入（上面右图的隐藏层有个环）；
以时间步对RNN进行展开后的单层网络结构
- RNN 实际运行时，是按时间一步步算的（时间步 t1→t2→t3… ）。为了方便理解，我们把“循环的隐藏层”拆成“多个隐藏层，按时间串联”；
- 展开后的RNN网络结构特点：
  1. 输入有两个：数据端输入（当前时间步的新词、新价格）、隐藏层输入（上一时间步隐藏层记住的信息）；
    - 如果是第一个时间步，对于隐藏层的输入，输入的是初始化的隐藏层状态 $h_0$ ；
  2. 输出有两个：数据端输出（当前时间步的预测结果）、隐藏层输出（传给下一时间步，继续当“记忆”）。

1.2 作用

作用：
- RNN 结构能够连续性地输入序列数据，进行特征提取。比如：人类的语言、语音特别适合用RNN进行处理；
- RNN 广泛应用于NLP领域的各项任务，如文本分类、情感分析、意图识别、机器翻译等；
例：用户意图识别
- 第一步：用户输入“What time is it ?”，先进行分词。RNN是一个时间步一个时间步地接收输入数据，所以每次只接收一个单词处理；
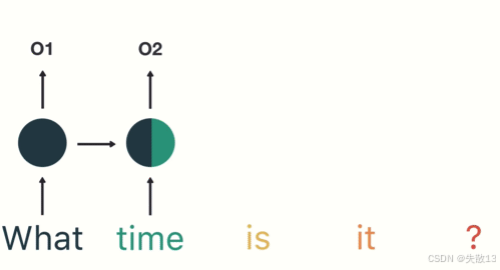
- 第二步：首先将单词"What"输送给RNN，它将产生一个输出O1；
- 第三步：继续将单词“time”输送给RNN，RNN不仅利用"time"来产生输出O2，还使用上一个时间步的隐藏层输出的O1作为输入信息；
  - 所以下图中，第一个隐藏层向右的箭头输出的数据，可以理解为是向上的箭头输出的数据的副本；
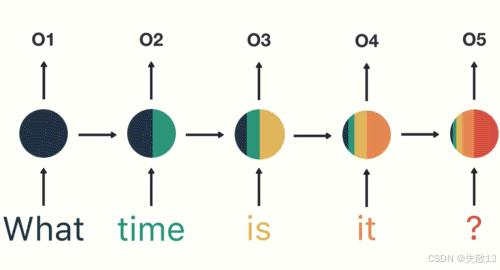
- 第四步：重复这样的步骤，直到处理完所有的单词；
- 第五步：最后，将最终的隐藏层输出O5进行处理来解析用户意图；

1.3 分类

按照输入和输出的角度进行分类
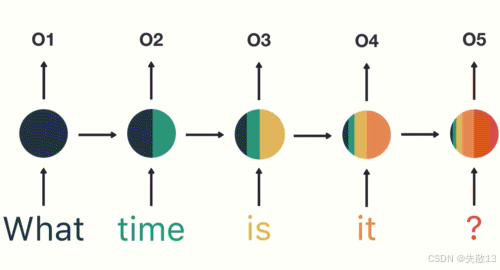
- N vs N – RNN：
  - 输入N个序列，输出N个序列。输入和输出序列是等长的；
  - 写诗、写对联等固定场景表达；
- N vs 1 – RNN：
  - 输入N个序列，输出1个的值。输入是一个序列，而要求输出是一个单独的值而不是序列；
  - 还要使用s igmoid或者softmax进行处理；
  - 情感分类、文本识别；
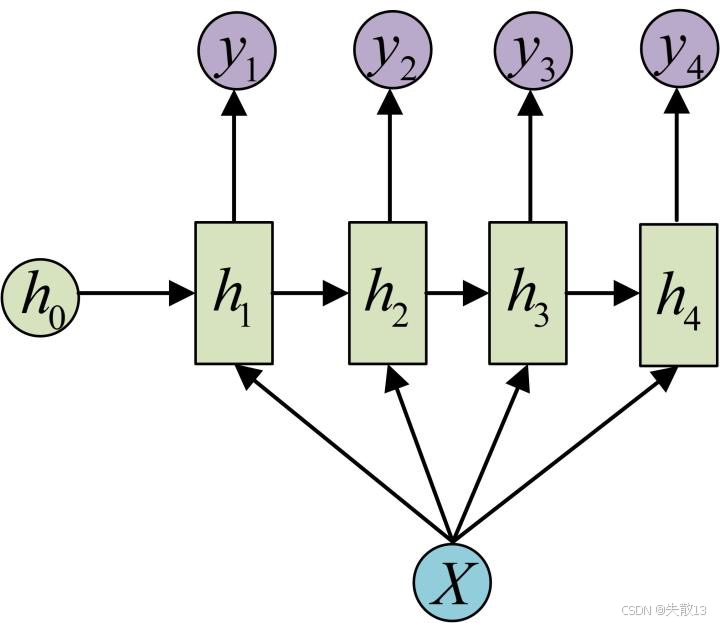
- 1 vs N – RNN：
  - 输入1个序列，输出N个的值。输入是一个值，使该输入作用于每次的输出上；
  - 看图说话；
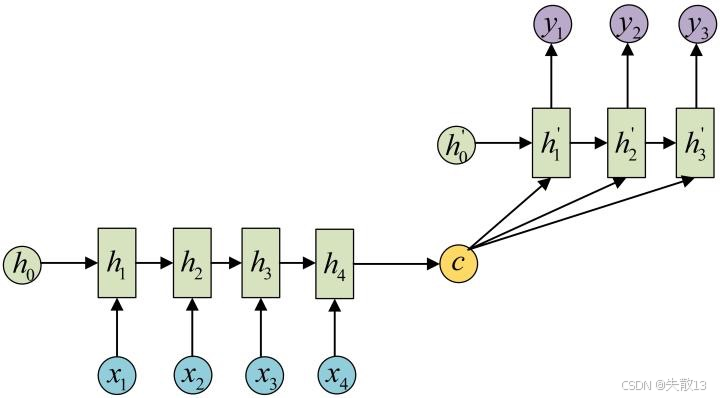
- N vs M – RNN：也称作seq2seq（序列到序列）模型
  - 输入N个序列，输出M个序列；
  - 结构特点：编码器、解码器、语义向量C，编码器和解码器的内部结构都是某类RNN；
  - 输入数据首先通过编码器，最终输出一个语义变量c，再将隐含变量作用在解码器进行解码的每一步上，得到输出结果；
  $h_0$ 是什么？
  - $h_0$ 是 RNN 开始处理输入序列时，隐藏层的初始状态；
  - 一般情况下， $h_0$ 会被初始化为全零向量，但在一些复杂的场景或预训练模型中，也可能被初始化为经过训练得到的特定值，从而为后续的隐藏状态计算提供一个更有意义的起始点；
  $h_0'$ 是什么？
  - 解码器开始生成输出序列时，需要一个初始的隐藏状态，这个状态就是 $h_0'$ ；
  - 最简单的 seq2seq， $h_0'$ 直接用编码器最后一个时间步的隐藏状态 $h_4$ 初始化；
  - 复杂点的模型（比如加了 Attention）， $h_0'$ 可能结合编码器的多个隐藏状态，甚至随机初始化，但核心逻辑不变：给解码器一个 “初始记忆”，让它知道 “要生成的内容和输入序列啥关系”；
  编码器（Encoder）——把输入序列压缩成语义向量
  - 输入：序列数据（比如中文句子的词序列 $x_1, x_2, x_3, x_4$ ）；
  - 过程：用 RNN（ $h_1→h_2→h_3→h_4$ ）逐步处理每个词，把整个序列的信息压缩成一个“语义向量 $C$ ”（可以理解成“把整段话的意思浓缩成一个向量”）；
  - 关键：语义向量 $C$ 要包含输入序列的全部关键信息，后续解码器全靠它“还原”成输出序列；
  解码器（Decoder）——把语义向量，还原成输出序列
  - 输入：语义向量 $C$ + 解码器自己的“隐藏状态”（ $h'_1, h'_2, h'_3$ ）；
  - 过程：解码器也是 RNN，每一步用 $C$ 和“上一步的隐藏状态”，生成一个输出（比如一个英文词 $y_1, y_2, y_3$ ），并更新自己的隐藏状态，直到输出完整序列；
  - 关键：解码器像个“翻译器”，拿着 $C$ （浓缩的语义），一步步“吐出”目标序列（比如英文句子）；
  “语义向量 $C$ ”——承上启下的桥梁
  - 作用：把输入序列（可能很长）的信息，压缩成固定长度的向量，让解码器能基于它生成任意长度的输出序列；
  - 缺点与改进：早期 seq2seq 用“一个 $C$ 包打天下”，但长序列时容易“信息丢失”（比如翻译长句子，前面的词信息会被后面的覆盖）。后来的 Attention（注意力机制） 就是为解决这问题，让解码器“动态关注 $C$ 里的不同部分”；
  - 机器翻译、阅读理解、文本摘要……因其输入输出不受限制，如今也是最广泛使用的RNN模型；
按照RNN的内部构造进行分类
- 传统RNN
- LSTM
- Bi-LSTM
- GRU
- Bi-GRU

2 传统RNN

2.1 RNN内部结构分析

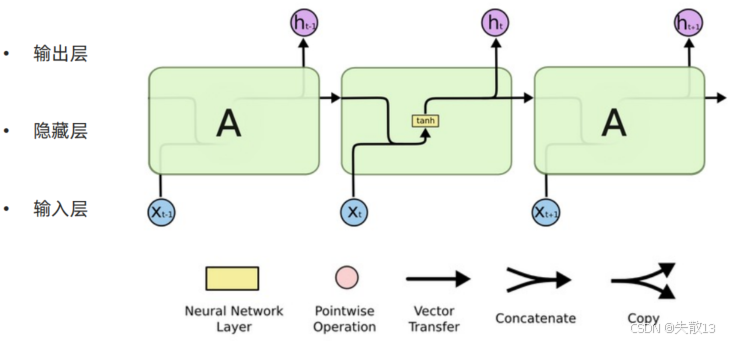
RNN内部结构图：
- 核心设计：同一隐藏层，时间步循环；
- 模块 A：是 RNN 的隐藏层核心计算单元，包含“全连接 + 激活函数”（比如 tanh）；
- 循环过程：
  - 上一时间步的隐藏层输出 $h_{t-1}$ ，会作为当前时间步的输入，和新数据 $x_t$ “融合”在一起后计算，得到新的张量 $x_t,h_{t-1}]$ ；
  - 这个 $x_t,h_{t-1}]$ 将通过一个全连接层，该层使用tanh作为激活函数，最终得到该时间步的输出，即 $h_t$ ；
  - 然后 $h_t$ 和 $x_{t+1}$ 将一起作为下一个时间步的输入；
- 为什么要“循环”？
  - 普通神经网络：输入→隐藏层→输出，“一锤子买卖”，记不住历史；
  - RNN：隐藏层自己“循环”，把历史信息存到 $h$ 里，让模型能“记住前面的内容”（比如句子前几个词的意思）；
- 三层结构：输入层 → 隐藏层 → 输出层
  - 输入层：接收当前时间步的数据 $x_t$ （比如句子里的一个词，股票的一个时间点价格）；
  - 隐藏层：用 $x_t$ 和 $h_{t-1}$ 计算新的 $h_t$ ，负责“存历史信息 + 处理新信息”；
  - 输出层：用 $h_t$ 生成当前时间步的输出（比如预测下一个词，预测下一时间点价格）；
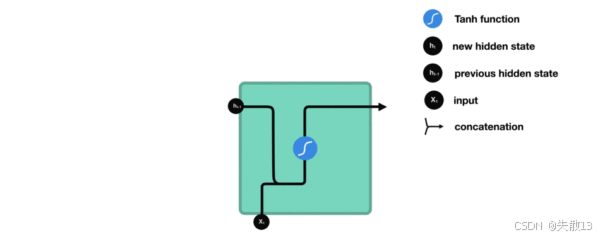
隐藏层中是怎么计算的？
- 学术界公式（简化版）
  $h_t = \tanh(W_e [X_t, h_{t-1}] + b_t)$
  - $X_t, h_{t-1}]$ ：把“当前输入 $X_t$ ”和“历史隐藏状态 $h_{t-1}$ ”拼接成一个长向量；
  - $W_e$ ：权重矩阵，给拼接后的向量“加权求和”（不同位置的信息，权重不同）；
  - $b_t$ ：偏置项，调整计算结果；
  - $tanh⁡\tanh$ ：激活函数，给结果加“非线性”（否则多层 RNN 会退化成单层线性变换）；
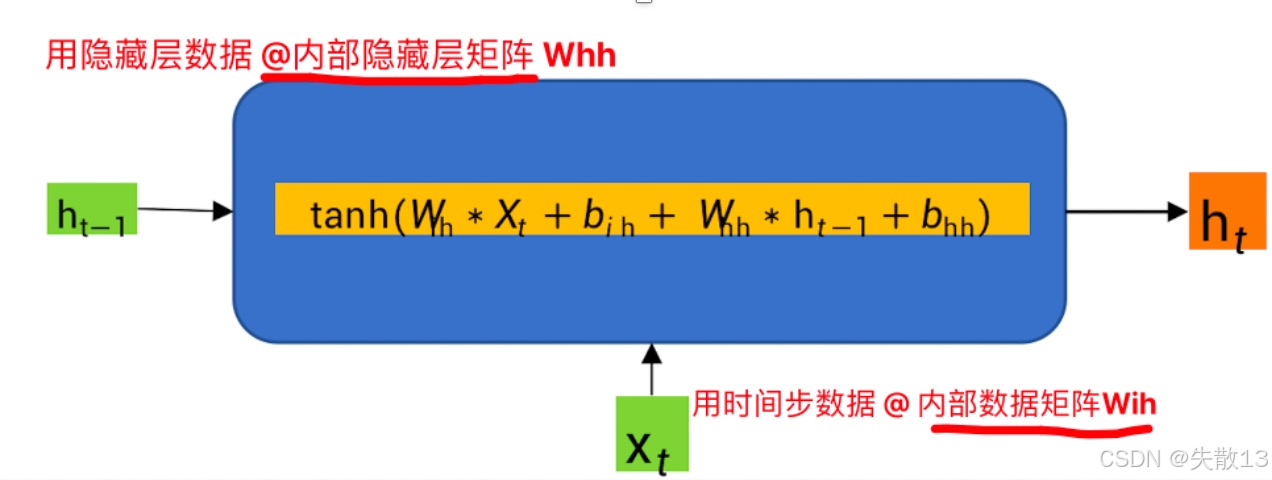
- 工业界实现（PyTorch 版）
  $h_t = \tanh(W_{in} * X_t + b_{in} + W_{hn} * h_{t-1} + b_{hn})$
  - 工业界为了灵活控制“输入权重”和“历史权重”，把 $W_e$ 拆成 $W_{in}$ （输入的权重） 和 $W_{hn}$ （历史隐藏状态的权重），偏置项也拆成 $b_{in}$ 和 $b_{hn}$ ；
  - 本质和简化版一样，只是更细粒度地控制“新信息”和“历史信息”的影响力；
- 不管公式咋变，核心都是：
  $\text{新 } h_t = \text{激活函数}(\text{当前输入的加权} + \text{历史隐藏状态的加权} + \text{偏置})$
激活函数 tanh 的作用
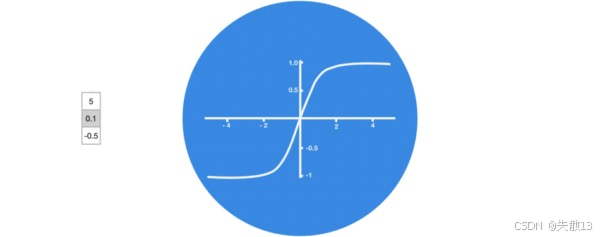
- $tanh⁡\tanh$ 函数的输出范围是 (-1, 1)；
- 为什么要压缩？
  - 如果不压缩，隐藏状态 $h_t$ 的数值会“越来越大”（因为每一步都加权求和），导致 梯度爆炸（训练时参数更新幅度过大，模型直接崩溃）；
  - 用 $tanh⁡\tanh$ 把数值锁在 (-1, 1)，能一定程度上稳定训练；
对比其他激活函数（比如 ReLU）
- $tanh⁡\tanh$ 是“老一代”激活函数，现在 RNN 变体（比如 LSTM）常用 ReLU 或 GELU，但核心逻辑不变：给隐藏状态加“非线性”，同时控制数值范围；
- 小缺点： $tanh⁡\tanh$ 在“-1 附近”梯度很小，容易导致梯度消失（训练时，历史信息传不到后面时间步）。这也是 LSTM/GRU 诞生的原因之一（用门控机制解决梯度消失）。

2.2 API

2.2.1 API简介

RNN 的API可以提取文本序列的特征；
在torch.nn工具包之中，通过torch.nn.RNN可调用；
案例需求：
- 输入：3 个批次（即 3 条文本），每个批次 1 个单词（序列长度 1），每个单词用 5 个特征表示（input_size=5）；
- 输出：每个单词被编码成 6 个特征。

2.2.2 参数

# 1. 初始化 RNN 模型
#    - input_size=5：输入序列中每个元素的特征维度是 5（比如每个词用 5 个数值表示）
#    - hidden_size=6：隐藏层神经元的个数是 6（每个时间步输出 6 维特征）
#    - num_layers=1：隐藏层的层数是 1（基础单向 RNN）
rnn = nn.RNN(5, 6, 1)# 2. 构造输入数据
#    - 形状是 (seq_len, batch_size, input_size) = (1, 3, 5)
#    - seq_len=1：每个批次的序列长度是 1（比如每个批次只有 1 个单词）
#    - batch_size=3：有 3 个批次（即 3 条平行的输入数据）
#    - input_size=5：每个元素的特征维度是 5（和 RNN 的 input_size 对应）
input = torch.randn(1, 3, 5)# 3. 构造初始隐藏状态 h0
#    - 形状是 (num_layers, batch_size, hidden_size) = (1, 3, 6)
#    - num_layers=1：隐藏层的层数是 1（和 RNN 的 num_layers 对应）
#    - batch_size=3：批次大小是 3（和输入数据的批次对应）
#    - hidden_size=6：隐藏层神经元个数是 6（和 RNN 的 hidden_size 对应）
h0 = torch.randn(1, 3, 6)# 4. 执行 RNN 前向计算
#    - 将输入数据 input 和初始隐藏状态 h0 传入 RNN
#    - 输出包含两部分：
#      1) output：每个时间步的隐藏层输出，形状 (seq_len, batch_size, hidden_size) = (1, 3, 6)
#      2) hn：最终的隐藏层状态，形状 (num_layers, batch_size, hidden_size) = (1, 3, 6)
output, hn = rnn(input, h0)# 5. 打印输出结果
#    - 打印 output 的形状和具体值，查看每个时间步的隐藏层输出
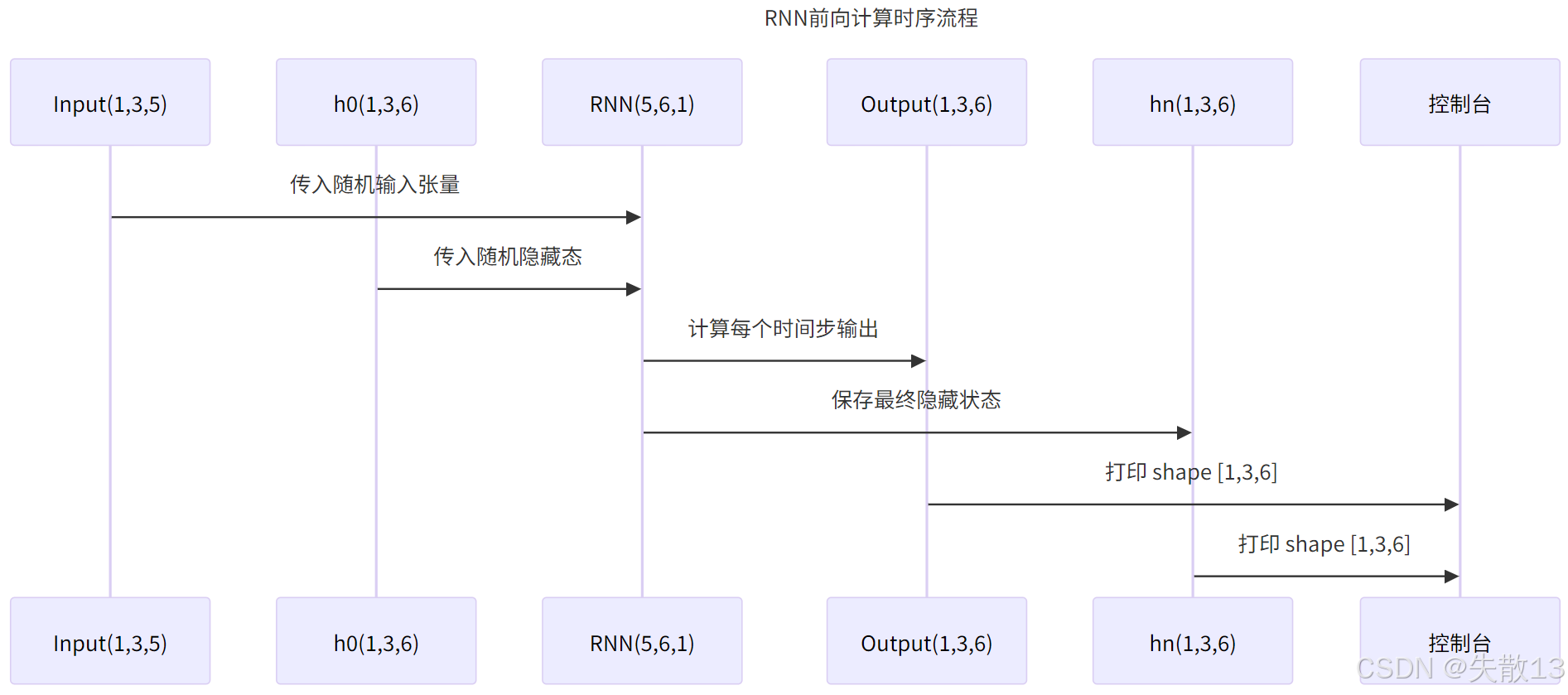
print('output-->', output.shape, '\n', output)
#    - 打印 hn 的形状和具体值，查看最终的隐藏层状态（和 output[-1] 结果一致，因为是单层单向 RNN）
print('hn-->', hn.shape, '\n', hn)

output--> torch.Size([1, 3, 6]) tensor([[[ 0.6236,  0.5790, -0.2830,  0.4407,  0.7677,  0.1880],[ 0.5468,  0.4484, -0.5309,  0.7859,  0.8436,  0.6732],[ 0.1489,  0.3383,  0.0618,  0.0298,  0.3531,  0.0852]]],grad_fn=<StackBackward0>)
hn--> torch.Size([1, 3, 6]) tensor([[[ 0.6236,  0.5790, -0.2830,  0.4407,  0.7677,  0.1880],[ 0.5468,  0.4484, -0.5309,  0.7859,  0.8436,  0.6732],[ 0.1489,  0.3383,  0.0618,  0.0298,  0.3531,  0.0852]]],grad_fn=<StackBackward0>)

在这里插入图片描述

2.2.3 调整输入尺寸

# 1. 初始化 RNN 模型
#    - input_size=55：输入序列中每个元素的特征维度是 55（比如每个词用 55 个数值表示）
rnn = nn.RNN(55, 6, 1)# 2. 构造输入数据
#    - input_size=55：每个元素的特征维度是 55（和 RNN 的 input_size 对应）
input = torch.randn(1, 3, 55)# 3. 构造初始隐藏状态 h0
h0 = torch.randn(1, 3, 6)# 4. 执行 RNN 前向计算
output, hn = rnn(input, h0)# 5. 打印输出结果的形状
print('output-->', output.shape)
print('hn-->', hn.shape)

在这里插入图片描述

2.2.4 调整输出尺寸

# 1. 初始化 RNN 模型
#    - hidden_size=66：隐藏层神经元的个数是 66（每个时间步输出 66 维特征）
rnn = nn.RNN(5, 66, 1)# 2. 构造输入数据
input = torch.randn(1, 3, 5)# 3. 构造初始隐藏状态 h0
#    - hidden_size=66：隐藏层神经元个数，和 RNN 模型初始化时的 hidden_size 对应
h0 = torch.randn(1, 3, 66)# 4. 执行 RNN 前向计算
output, hn = rnn(input, h0)# 5. 打印输出结果的形状信息
print('output-->', output.shape)
print('hn-->', hn.shape)

在这里插入图片描述

2.2.5 调整输入数据长度

# 1. 初始化 RNN 模型
rnn = nn.RNN(5, 6, 1)# 2. 构造输入数据
#    - seq_len=11：每个批次的序列长度是 11（比如每个批次有 11 个单词）
input = torch.randn(11, 3, 5)# 3. 构造初始隐藏状态 h0
h0 = torch.randn(1, 3, 6)# 4. 执行 RNN 前向计算
output, hn = rnn(input, h0)# 5. 打印输出结果的形状
print('output-->', output.shape)
print('hn-->', hn.shape)

在这里插入图片描述

2.2.6 调整数据批次

# 1. 初始化 RNN 模型
rnn = nn.RNN(5, 66, 1)# 2. 构造输入数据
#    - batch_size=33：表示有 33 个批次，也就是同时处理 33 组平行的输入数据
input = torch.randn(1, 33, 5)# 3. 构造初始隐藏状态 h0
#    - batch_size=33：批次大小，与输入数据的批次数量一致
h0 = torch.randn(1, 33, 66)# 4. 执行 RNN 前向计算
output, hn = rnn(input, h0)# 5. 打印输出结果的形状信息
print('output-->', output.shape)
print('hn-->', hn.shape)

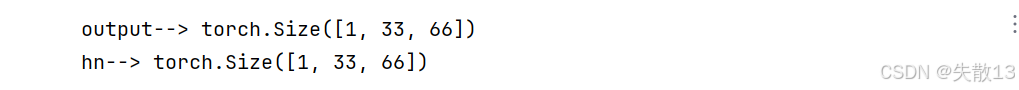
在这里插入图片描述

2.2.7 调整模型隐藏层个数

# 1. 初始化多层 RNN 模型
#    - num_layers=2：隐藏层的**层数是 2**（构建多层 RNN，这里是 2 层单向 RNN 堆叠）
rnn = nn.RNN(5, 6, 2)# 2. 构造输入数据
input = torch.randn(1, 3, 5)# 3. 构造初始隐藏状态 h0
#    - num_layers=2：隐藏层的层数是 2（和 RNN 模型的 num_layers 对应）
h0 = torch.randn(2, 3, 6)# 4. 执行 RNN 前向计算
output, hn = rnn(input, h0)# 5. 打印输出结果
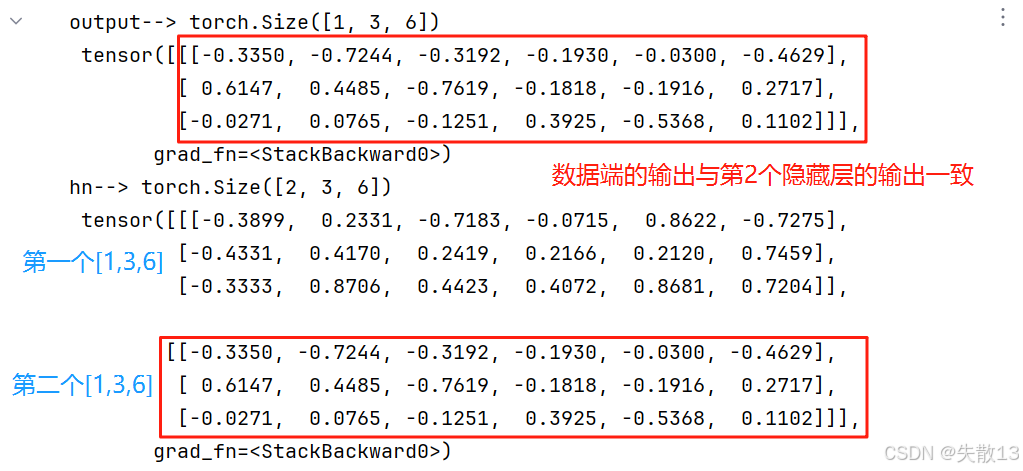
print('output-->', output.shape, '\n', output)
print('hn-->', hn.shape, '\n', hn)# 注释说明
# 注1：当 `num_layers=1` 时，output 和 hn[-1]（最后一层的最终状态）结果一致
# 注2：当 `num_layers>1` 时，output 是最后一层每个时间步的输出，hn 包含所有层的最终状态
#      因此，output 和 hn[-1]（最后一层的最终状态）结果一致

在这里插入图片描述

输出结果解读：
- 1 层隐藏层：输入 → 隐藏层 1 → 输出（output = 隐藏层 1 输出）；
- 2 层隐藏层：输入 → 隐藏层 1 → 隐藏层 2 → 输出（output = 隐藏层 2 输出）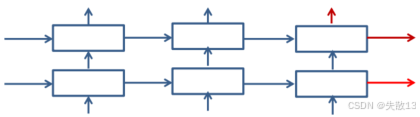
- n 层隐藏层：输入 → 隐藏层 1 → 隐藏层 2 → … → 隐藏层 n → 输出（output = 隐藏层 n 输出）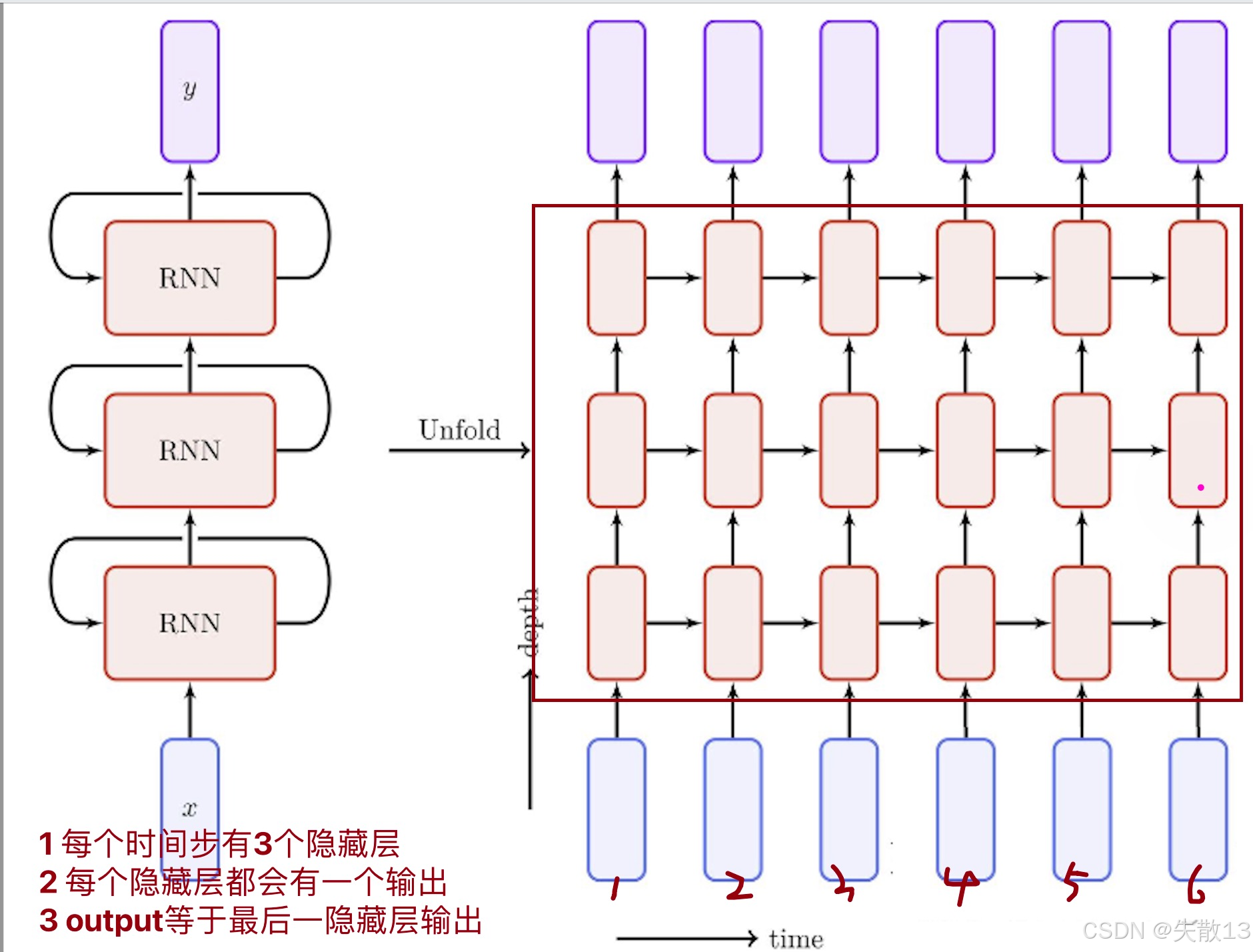
总结：当隐藏层个数配置成 n 时，output 的结果和最后一个隐藏层输出一致。

2.2.8 调整数据批次数在前

# 1. 初始化 RNN 模型，设置 batch_first=True
#    - batch_first=True：
#      作用：让输入和输出的张量形状以 batch_size 开头（即形状为 [batch_size, seq_len, input_size]）
#      注意：仅影响 input 和 output 的形状，不影响 h0、hn 的形状（它们仍以 num_layers 开头）
my_rnn = nn.RNN(5, 6, 1, batch_first=True)# 2. 构造输入数据
#    - 形状是 (batch_size, seq_len, input_size) = (3, 1, 5)
#    - 因为 batch_first=True，所以第一维是 batch_size（3 个批次）
#    - seq_len=1（每个批次的序列长度是 1），input_size=5（每个元素的特征维度）
input = torch.randn(3, 1, 5)# 3. 构造初始隐藏状态 h0
#    - 形状是 (num_layers, batch_size, hidden_size) = (1, 3, 6)
#    - batch_first=True 不影响 h0 的形状，仍以 num_layers 开头
h0 = torch.randn(1, 3, 6)# 4. 执行 RNN 前向计算
#    - 输入数据 input 形状 (3, 1, 5)（符合 batch_first=True 的要求）
#    - 初始隐藏状态 h0 形状 (1, 3, 6)（不受 batch_first 影响）
#    - 输出包含两部分：
#      1) output：形状 (batch_size, seq_len, hidden_size) = (3, 1, 6)（因为 batch_first=True）
#      2) hn：形状 (num_layers, batch_size, hidden_size) = (1, 3, 6)（不受 batch_first 影响）
output, hn = my_rnn(input, h0)# 5. 打印输出结果的形状
print('output-->', output.shape)
print('hn-->', hn.shape)# 代码核心逻辑：
# batch_first=True 的作用是让 input 和 output 的形状以 batch_size 开头（更符合直观习惯）
# 但 h0 和 hn 的形状仍保持 (num_layers, batch_size, hidden_size)，不受影响

在这里插入图片描述

2.2.9 输入数据的两种方式

# 1. 初始化 RNN 模型
rnn = nn.RNN(5, 6, 1, batch_first=True)# 2. 构造随机输入数据
#    - 形状：(batch_size, seq_len, input_size) = (1, 10, 5)
#    - 含义：1 个批次，10 个字符（序列长度 10），每个字符用 5 维特征表示
input = torch.randn(1, 10, 5)# 3. 初始化隐藏状态
#    - 形状：(num_layers, batch_size, hidden_size) = (1, 1, 6)
#    - 用全 0 初始化隐藏状态（也可用随机值）
hidden = torch.zeros(1, 1, 6)# -------------------- 方式1：逐个时间步输入数据（字符） --------------------
# 逻辑：手动遍历每个时间步，逐个字符输入 RNN，手动传递隐藏状态
for i in range(input.shape[1]):  # input.shape[1] = 10（序列长度，共 10 个时间步）# 取出当前时间步的输入（单个字符）# input[:, i, :] 取出第 i 个时间步的特征，形状 (1, 5)# 但 RNN 要求输入形状 (batch_size, seq_len, input_size)，所以用 unsqueeze 补全维度tmp = input[:, i, :].unsqueeze(1)  # 补成 (1, 1, 5)# 输入给 RNN：当前时间步输入 + 上一时间步的隐藏状态# rnn 输出：当前时间步的 output（形状 (1, 1, 6)） + 更新后的 hidden（形状 (1, 1, 6)）output, hidden = rnn(tmp, hidden)# 打印每个时间步的输出（验证逐个传递的过程）print(f'{i + 1} -->', output.shape, output)# -------------------- 方式2：一次性输入全部数据 --------------------
# 逻辑：直接把整个序列（10 个字符）输入给 RNN，模型内部自动遍历时间步，传递隐藏状态
# 重新初始化隐藏状态（避免受方式1影响）
hidden = torch.zeros(1, 1, 6)# 一次性输入整个序列（形状 (1, 10, 5)）
output, hidden = rnn(input, hidden)# 打印一次性输入数据的输出（验证模型内部自动遍历的结果）
print('一次性输入数据 output\n', output.shape, output)

1 --> torch.Size([1, 1, 6]) tensor([[[ 0.4178, -0.2417,  0.3189,  0.6201, -0.3831,  0.6262]]],grad_fn=<TransposeBackward1>)
2 --> torch.Size([1, 1, 6]) tensor([[[-0.6708,  0.1563, -0.7931, -0.5868, -0.4512, -0.0880]]],grad_fn=<TransposeBackward1>)
3 --> torch.Size([1, 1, 6]) tensor([[[ 0.2514,  0.5975, -0.7491,  0.3919, -0.4360, -0.0557]]],grad_fn=<TransposeBackward1>)
4 --> torch.Size([1, 1, 6]) tensor([[[-0.5499,  0.7572, -0.8983,  0.0600,  0.2337, -0.3928]]],grad_fn=<TransposeBackward1>)
5 --> torch.Size([1, 1, 6]) tensor([[[-0.5120,  0.6703,  0.1447,  0.5362, -0.5573,  0.1616]]],grad_fn=<TransposeBackward1>)
6 --> torch.Size([1, 1, 6]) tensor([[[-0.5205,  0.7027, -0.4184,  0.3433, -0.4837, -0.4589]]],grad_fn=<TransposeBackward1>)
7 --> torch.Size([1, 1, 6]) tensor([[[-0.8803,  0.8959, -0.7245, -0.2207,  0.3849, -0.4234]]],grad_fn=<TransposeBackward1>)
8 --> torch.Size([1, 1, 6]) tensor([[[-0.6703,  0.8615, -0.5916, -0.0171, -0.4583, -0.3254]]],grad_fn=<TransposeBackward1>)
9 --> torch.Size([1, 1, 6]) tensor([[[-0.8539,  0.7584,  0.4446,  0.7087, -0.3283, -0.0868]]],grad_fn=<TransposeBackward1>)
10 --> torch.Size([1, 1, 6]) tensor([[[-0.7833,  0.4795, -0.5264, -0.5058, -0.0571, -0.1314]]],grad_fn=<TransposeBackward1>)
一次性输入数据 outputtorch.Size([1, 10, 6]) tensor([[[ 0.4178, -0.2417,  0.3189,  0.6201, -0.3831,  0.6262],[-0.6708,  0.1563, -0.7931, -0.5868, -0.4512, -0.0880],[ 0.2514,  0.5975, -0.7491,  0.3919, -0.4360, -0.0557],[-0.5499,  0.7572, -0.8983,  0.0600,  0.2337, -0.3928],[-0.5120,  0.6703,  0.1447,  0.5362, -0.5573,  0.1616],[-0.5205,  0.7027, -0.4184,  0.3433, -0.4837, -0.4589],[-0.8803,  0.8959, -0.7245, -0.2207,  0.3849, -0.4234],[-0.6703,  0.8615, -0.5916, -0.0171, -0.4583, -0.3254],[-0.8539,  0.7584,  0.4446,  0.7087, -0.3283, -0.0868],[-0.7833,  0.4795, -0.5264, -0.5058, -0.0571, -0.1314]]],grad_fn=<TransposeBackward1>)

2.3 优缺点

优点：
- 内部结构简单，对计算资源要求低；
  - RNN变体：LSTM和GRU模型的参数总量少了很多；
- 在短序列任务上性能和效果都表现优异；
缺点：长序列文本特征提取效果差。过长的序列易导致梯度的计算异常，发生梯度消失或爆炸。

3 LSTM

3.1 概念

LSTM（Long Short-Term Memory）也称长短时记忆结构
- 它是传统RNN的变体
- 与经典RNN相比，能够有效捕捉长序列之间的语义关联，缓解梯度消失或爆炸现象
结构说明：
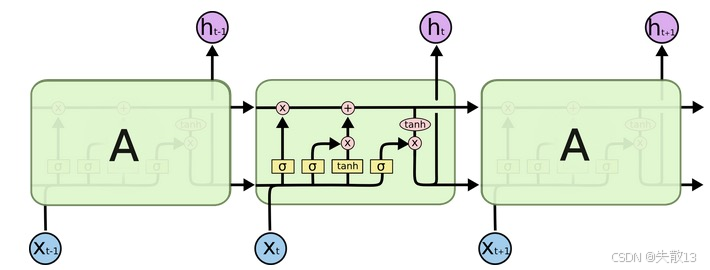
- 由输入层、隐藏层、输出层组成；
- 每个时间步有三个输入：数据端输入，上一个时间步细胞状态 $C_{t-1}$ ，上一个时间步的 $h_{t-1}$
- 每个时间步有三个输出：数据端输出，本时间步细胞状态 $C_{t}$ ，本时间步的 $h_{t}$
- LSTM结构更加复杂，内部有3个门和1个细胞状态：遗忘门、输入门、细胞状态、输出门
RNN 最大的痛点：序列过长时，隐藏层的历史信息会“被冲刷掉”（梯度消失），导致模型记不住早期内容（比如长句子的开头）；
LSTM 用细胞状态 $C_t$ + 三门控，让信息能“选择性记住/遗忘”，解决梯度消失问题。

3.2 内部结构

LSTM 通过遗忘门（丢历史）→ 输入门（存新信息）→ 细胞状态更新（历史+新信息）→ 输出门（选输出）的流程，让模型能选择性记住长期信息，解决了 RNN 梯度消失的问题，特别适合处理长序列任务（比如文本翻译、时间序列预测）；
遗忘门（Forget Gate）——决定历史细胞状态要丢多少
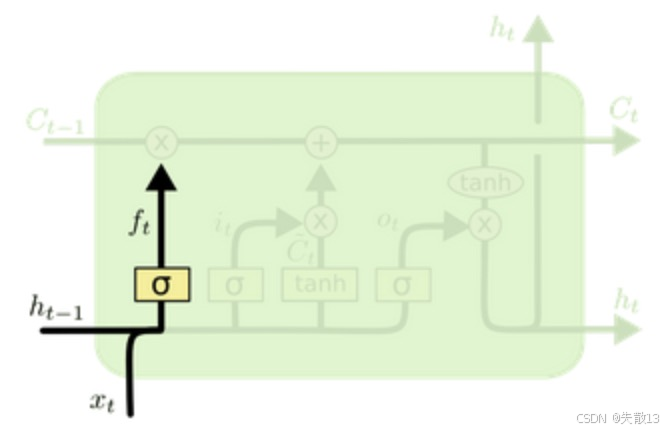
- 公式：
  $f_t = \sigma(W_f [h_{t-1}, x_t] + b_f)$
  - $h_{t-1}, x_t]$ ：把上一时间步的隐藏状态 $h_{t-1}$ 和当前输入 $x_t$ 拼接；
  - $W_f, b_f$ ：权重和偏置，通过训练得到；
  - $σ\sigma$ ：sigmoid 激活函数（输出 0~1 之间的数）；
- $f_t$ 是一个遗忘比例
  - $f_t$ 接近 1 → 保留大部分历史细胞状态 $C_{t-1}$ ；
  - $f_t$ 接近 0 → 遗忘大部分历史细胞状态 $C_{t-1}$ ；
- 历史细胞状态经过遗忘门过滤后，剩下的部分：
  $f_t * C_{t-1}$
输入门（Input Gate）——决定新信息要存多少
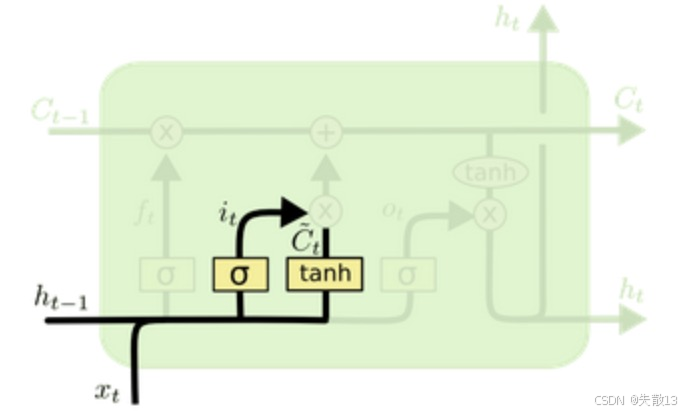
- 公式：
  $i_t = \sigma(W_i [h_{t-1}, x_t] + b_i) （输入门控制要不要存新信息） \\ \tilde{C_t} = \tanh(W_c [h_{t-1}, x_t] + b_c) （生成新的候选细胞状态）$
  - $i_t$ 是新信息的保留比例（0~1 之间）；
  - $Ct~\tilde{C_t}$ 是“当前输入 $x_t$ 生成的新信息”（tanh 把值压缩到 -1~1）；
  - $it∗Ct~i_t * \tilde{C_t}$ 表示新信息经过输入门过滤后，要加入细胞状态的部分；
细胞状态更新——历史 + 新信息，得到新细胞状态
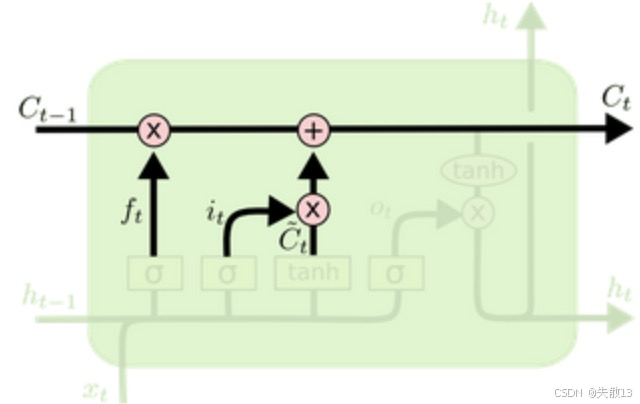
- 公式：
  $C_t = f_t * C_{t-1} + i_t * \tilde{C_t}$
- 作用：把遗忘门过滤后的历史细胞状态和输入门过滤后的新候选状态相加，得到新的细胞状态 $C_t$ ；
- 这一步是 LSTM 的核心——细胞状态 $C_t$ 实现了“长期记忆”的更新，让重要信息能跨时间步传递，不被梯度消失冲刷；

输出门（Output Gate）——决定细胞状态要输出多少给隐藏层
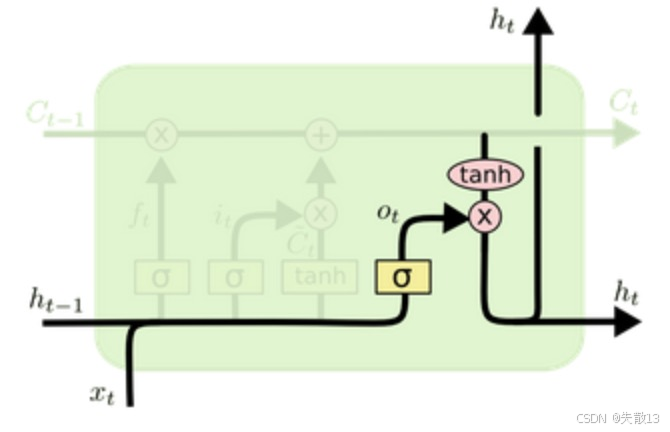
- 公式：
  $o_t = \sigma(W_o [h_{t-1}, x_t] + b_o) （输出门控制细胞状态有多少要输出）\\h_t = o_t * \tanh(C_t) （细胞状态经过 tanh 压缩后，按输出门比例输出）$
  - $o_t$ 是“细胞状态的输出比例”（0~1 之间）；
  - $tanh(C_t)$ 把细胞状态 $C_t$ 压缩到 -1~1；
  - $h_t$ 是当前时间步的隐藏层输出，同时作为下一时间步的 $h_{t+1}$ ；
- 输出门决定“细胞状态 $C_t$ 有多少要传递给隐藏层 $h_t$ ”，影响当前输出和下一时间步的输入；

LSTM 核心优势：细胞状态 $C_t$ 实现长期记忆
- 普通 RNN：隐藏状态 $h_t$ 直接传递，历史信息易丢失；
- LSTM：细胞状态 $C_t$ 用“三门控”选择性保留/更新，让重要信息能跨多个时间步传递（比如长句子的开头信息，能被结尾的 LSTM 记住）。

3.3 双向BI-LSTM模型

双向 LSTM 要解决的问题
- 普通 LSTM（或 RNN）处理序列时，只能“从左到右”看历史信息（比如处理“我爱中国”，看到“国”时，只能基于“我→爱→中”的历史）；
- 但很多任务需要未来信息辅助当前判断（比如填空“我__中国”，需要看后面的“中国”才能确定填“爱”）；
- 双向 LSTM 的思路：同时从左到右和从右到左跑两个 LSTM，把结果拼接，让模型同时看到历史和未来信息；
结构拆解
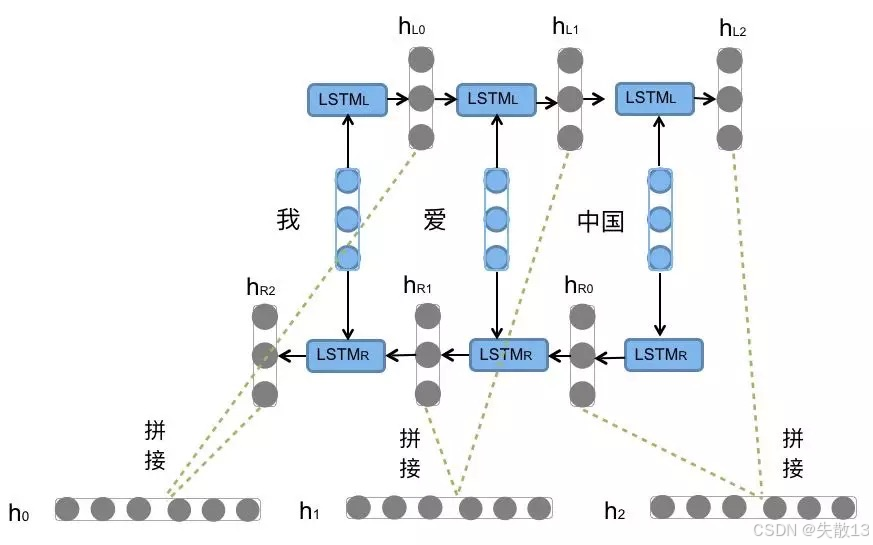
- 两个方向的 LSTM
  - 正向 LSTM（LSTM_L）：从左到右处理序列（我→爱→中→国），每个时间步的隐藏状态记为 $h_{L0}, h_{L1}, h_{L2}$ ；
  - 反向 LSTM（LSTM_R）：从右到左处理序列（国→中→爱→我），每个时间步的隐藏状态记为 $h_{R0}, h_{R1}, h_{R2}$ ；
- 隐藏状态拼接。对于每个时间步 $t$ （比如处理“爱”时）：
  - 正向 LSTM 输出 $h_{L1}$ （基于“我→爱”的历史）
  - 反向 LSTM 输出 $h_{R1}$ （基于“爱→中→国”的未来）
  - 拼接 $h_{L1}$ 和 $h_{R1}$ ，得到同时包含历史和未来信息的隐藏状态，作为当前时间步的最终输出
- 对应图中的流程
  - 输入序列：“我”、“爱”、“中国”（图里拆成“我”、“爱”、“中国”三个 token）
  - 正向 LSTM（上半部分）：从左到右跑，输出 $h_{L0}, h_{L1}, h_{L2}$
  - 反向 LSTM（下半部分）：从右到左跑，输出 $h_{R0}, h_{R1}, h_{R2}$
  - 每个时间步的输出：拼接正向和反向的隐藏状态（比如 $h_0 = [h_{L0}, h_{R0}]$ ）
特点
- 不改变 LSTM 内部结构：只是同时跑两个 LSTM（正向+反向），每个 LSTM 的内部逻辑（三门控）不变；
- 两次处理，拼接结果：对同一序列，正向和反向各跑一次，把两个方向的隐藏状态拼接，作为最终输出；
- 参数和计算量翻倍：因为有两个独立的 LSTM（正向和反向），所以参数数量（权重、偏置）和计算量都是普通 LSTM 的 2 倍
应用：
- 适合需要上下文全信息的任务
  - 自然语言处理：命名实体识别（比如识别“中国”是国家，需要前后文）、情感分析（比如“不开心”需要结合前后判断）；
  - 时间序列：股票预测（注意：此处股票的未来不可知，实际中更多是用双向看全局）；
- 不适合在线实时任务（比如实时翻译，未来信息不可得）。

3.4 API

import torch
import torch.nn as nn

# 1. 初始化 LSTM 模型
#    - input_size=5：表示输入序列中每个元素的特征维度是 5，即每个时间步输入数据的特征数量为 5
#    - hidden_size=6：隐藏层中 LSTM 单元的维度（也可理解为隐藏层神经元个数），决定了隐藏状态的维度
#    - num_layers=2：LSTM 隐藏层的层数，这里构建的是 2 层的 LSTM 结构，多层 LSTM 可提取更复杂特征
lstm = nn.LSTM(5, 6, 2)# 2. 构造输入数据
#    - 生成的张量形状为 (seq_len, batch_size, input_size) = (1, 3, 5)
#    - seq_len=1：每个批次对应的序列长度是 1，意味着每个批次里只有一个时间步的数据（例如一句话里只有一个词 ）
#    - batch_size=3：表示有 3 个批次，也就是同时处理 3 组平行的输入数据
#    - input_size=5：每个元素的特征维度是 5，要和 LSTM 初始化时设置的 input_size 保持一致
input = torch.randn(1, 3, 5)# 3. 构造初始隐藏状态和细胞状态
#    - LSTM 内部有两个状态：隐藏状态 h0 和细胞状态 c0，它们的形状都遵循 (num_layers, batch_size, hidden_size)
#    - num_layers=2：LSTM 隐藏层的层数，和模型初始化时的 num_layers 对应
#    - batch_size=3：批次大小，与输入数据的批次数量一致
#    - hidden_size=6：隐藏层神经元个数，和 LSTM 模型初始化时的 hidden_size 对应
h0 = torch.randn(2, 3, 6)  # 初始化隐藏状态
c0 = torch.randn(2, 3, 6)  # 初始化细胞状态，LSTM 特有，用于长期记忆的传递# 4. 执行 LSTM 前向计算
#    - 将构造好的输入数据 input 以及初始隐藏状态 h0、细胞状态 c0 传入实例化的 LSTM 模型
#    - LSTM 会依据其内部的门控机制（遗忘门、输入门、细胞状态更新、输出门 ）进行计算
#    - 输出包含三部分：
#      - output：每个时间步的隐藏层输出结果，形状为 (seq_len, batch_size, hidden_size) = (1, 3, 6)
#      - hn：最终的隐藏层状态，形状为 (num_layers, batch_size, hidden_size) = (2, 3, 6)，包含各层最后一个时间步的隐藏状态
#      - cn：最终的细胞状态，形状为 (num_layers, batch_size, hidden_size) = (2, 3, 6)，包含各层最后一个时间步的细胞状态
output, (hn, cn) = lstm(input, (h0, c0))# 5. 打印输出结果
#    - 打印 output 的形状和具体值，查看每个时间步的隐藏层输出情况
print('output-->', '\n', output.shape, '\n', output)
#    - 打印 hn 的形状和具体值，查看最终的隐藏层状态，它是各层最后时间步隐藏状态的集合
print('hn-->', '\n', hn.shape, '\n', hn)
#    - 打印 cn 的形状和具体值，查看最终的细胞状态，它是各层最后时间步细胞状态的集合，体现 LSTM 长期记忆的保留情况
print('cn-->', '\n', cn.shape, '\n', cn)

在这里插入图片描述

3.5 优缺点

优点：LSTM的门结构能够有效减缓长序列问题中可能出现的梯度消失或爆炸，虽然并不能杜绝这种现象，但在更长的序列问题上表现优于传统RNN；
缺点：由于内部结构相对较复杂，因此训练效率在同等算力下较传统RNN低很多。

4 GRU

4.1 概念

GRU（Gated Recurrent Unit）也称门控循环单元结构
- 它也是传统RNN的变体
- 同LSTM一样，能够有效捕捉长序列之间的语义关联，缓解梯度消失或爆炸现象
- 同时它的结构比LSTM更简单，但当然比RNN复杂
结构说明：
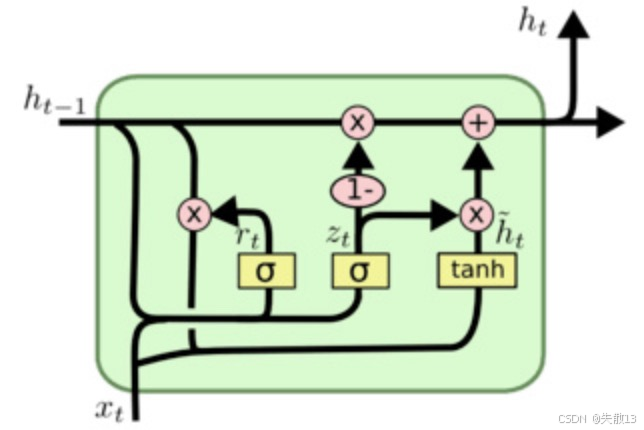
- 由输入层、隐藏层、输出层组成
- 同RNN，每个时间步有2个输入：数据端输入，上一个时间步的 $h_{t-1}$
- 同RNN，每个时间步有2个输出：数据端输出，本时间步的 $h_{t}$
- GRU结构有2个门：更新门、重置门
LSTM 用“三门控 + 细胞状态”解决了 RNN 的梯度消失，但结构复杂（参数多、计算慢）；
GRU 的思路：简化门控机制（两门控 + 合并细胞状态和隐藏状态），在保证效果的同时，减少参数和计算量。

4.2 内部结构

两门控：重置门（Reset Gate） + 更新门（Update Gate）
- 重置门（ $r_t$ ）：
  $r_t = \sigma(W_r [h_{t-1}, x_t] + b_r)$
  - 决定历史隐藏状态要遗忘多少（值接近 0 → 更多遗忘历史；接近 1 → 更多保留历史）；
  - 类比：LSTM 的遗忘门，但更简化；
- 更新门（ $z_t$ ）：
  $z_t = \sigma(W_z [h_{t-1}, x_t] + b_z)$
  - 决定新隐藏状态要保留多少历史/新信息（值接近 0 → 更多用新信息；接近 1 → 更多用历史）；
  - 类比：LSTM 的“输入门 + 输出门”的合并，用一个门控控制“历史 vs 新信息”的比例；
隐藏状态更新。候选隐藏状态（ $ht~\tilde{h_t}$ ）：
$\tilde{h_t} = \tanh(W [r_t * h_{t-1}, x_t] + b)$
- 用重置门过滤后的历史状态（ $r_t * h_{t-1}$ ）和当前输入 $x_t$ ，生成新信息；
最终隐藏状态（ $h_t$ ）：
$h_t = (1 - z_t) * h_{t-1} + z_t * \tilde{h_t}$
- 用更新门控制“历史隐藏状态 $h_{t-1}$ ”和“候选隐藏状态 $ht~\tilde{h_t}$ ”的比例：
  - $z_t$ 接近 1 → 更多保留历史 $h_{t-1}$ （长期记忆）；
  - $z_t$ 接近 0 → 更多用新信息 $ht~\tilde{h_t}$ （短期记忆）；
GRU 记忆机制的通俗解释：
- 重置门：决定“要不要忘记历史”：遇到新信息时，重置门说“历史信息要过滤多少”（比如遇到全新内容，重置门让模型少用历史）；
- 更新门：决定“新信息和历史信息的比例”：如果更新门接近 1，模型说“还是历史信息靠谱，多用历史”；如果接近 0，模型说“新信息更重要，多用新的”；
- 隐藏状态合并：GRU 没有单独的“细胞状态”，直接用 $h_t$ 同时承载“历史记忆”和“新信息”，通过两门控动态调整比例；

4.3 GRU vs LSTM

对比项	GRU	LSTM
门控数量	2 个（重置门 + 更新门）	3 个（遗忘门 + 输入门 + 输出门）
状态数量	1 个（隐藏状态 $h_t$ ）	2 个（隐藏状态 $h_t$ + 细胞状态 $C_t$ ）
核心逻辑	用两门控直接控制“历史 vs 新信息”的比例	用三门控 + 细胞状态管理“长期记忆”
参数与计算量	更少（适合轻量任务、大规模数据）	更多（适合需要精细记忆控制的任务）

4.4 API

import torch
import torch.nn as nn

# 1. 初始化 GRU 模型
#    - input_size=5：输入序列中每个元素的特征维度是 5（比如每个词用 5 个数值表示）
#    - hidden_size=6：隐藏层神经元的个数是 6（每个时间步输出 6 维特征）
#    - num_layers=2：隐藏层的层数是 2（2 层 GRU 堆叠，可提取更复杂特征）
mygru = nn.GRU(5, 6, 2)# 2. 构造输入数据
#    - 形状是 (seq_len, batch_size, input_size) = (1, 3, 5)
#    - seq_len=1：每个批次的序列长度是 1（比如每个批次只有 1 个单词）
#    - batch_size=3：有 3 个批次（即 3 条平行的输入数据）
#    - input_size=5：每个元素的特征维度是 5（和 GRU 的 input_size 对应）
input = torch.randn(1, 3, 5)# 3. 构造初始隐藏状态 h0
#    - 形状是 (num_layers, batch_size, hidden_size) = (2, 3, 6)
#    - num_layers=2：隐藏层的层数是 2（和 GRU 模型的 num_layers 对应）
#    - batch_size=3：批次大小是 3（和输入数据的批次对应）
#    - hidden_size=6：隐藏层神经元个数是 6（和 GRU 模型的 hidden_size 对应）
h0 = torch.randn(2, 3, 6)# 4. 执行 GRU 前向计算
#    - 将输入数据 input 和初始隐藏状态 h0 传入 GRU
#    - 输出包含两部分：
#      1) output：最后一层隐藏层每个时间步的输出，形状 (seq_len, batch_size, hidden_size) = (1, 3, 6)
#      2) hn：所有层的最终隐藏状态，形状 (num_layers, batch_size, hidden_size) = (2, 3, 6)
output, hn = mygru(input, h0)# 5. 打印输出结果
#    - 查看 output 的维度和内容，验证 GRU 的输出逻辑
print('output-->', '\n', output.shape, '\n', output)
#    - 查看 hn 的维度和内容，验证多层 GRU 的隐藏状态传递
print('hn-->', '\n', hn.shape, '\n', hn)

在这里插入图片描述

4.5 优缺点

优点：
- GRU和LSTM作用相同，在捕捉长序列语义关联时，能有效抑制梯度消失或爆炸，效果都优于传统RNN；
- 且计算复杂度相比LSTM要小；
缺点：
- GRU仍然不能完全解决梯度消失问题；
- 同时其作为RNN的变体，有着RNN结构本身的一大弊端，即不可并行计算，这在数据量和模型体量逐步增大的当下，是RNN发展的关键瓶颈；

注意上面提到的“并行计算”，指的是单个序列不可以并行计算

场景	能否并行	核心原因	典型实现
单个序列的时间步之间	串行（无法并行）	隐藏状态依赖上一时间步结果	天然限制
同一时间步的不同序列	并行（常用）	不同序列的隐藏状态相互独立	框架默认的批次并行
模型训练的参数 / 梯度计算	并行（复杂）	不同设备可分担计算 / 更新任务	分布式训练（如 `nn.DDP` ）
时间步展开的数学优化	理论可行（工程极难）	数学变换消解时间依赖	研究领域的尝试性方案