k 均值聚类算法总结
一、聚类算法简介
- 核心概念:聚类是无监督学习问题,即数据无标签,通过将相似数据分到一组实现分类。
- 主要难点:聚类结果的评估以及参数调整。
二、距离度量
- 欧式距离:最常见的距离度量,衡量多维空间中两点的绝对距离。
- 二维空间:d=(x1−x2)2+(y1−y2)2
- 三维空间:d=(x1−x2)2+(y1−y2)2+(z1−z2)2
- n 维空间:d=∑i=1n(x1i−x2i)2
- 曼哈顿距离:由赫尔曼・闵可夫斯基提出,指两点在标准坐标系上的绝对轴距总和。平面上两点(x1,y1)与(x2,y2)的曼哈顿距离公式为:d(i,j)=∣X1−X2∣+∣Y1−Y2∣。
三、k 均值算法
- 算法步骤
- 初始化:令t=0,随机选择k个样本点作为初始聚类中心m(0)=(m1(0),m2(0),⋯,mk(0))。
- 样本聚类:对于固定的类中心m(t)=(m1(t),⋯,mk(t)),计算每个样本到类中心的距离,将样本指派到最近中心的类中,构成聚类结果C(t)。
- 计算新中心:针对聚类结果C(t),计算各类中样本的均值,作为新的类中心m(t+1)=(m1(t+1),⋯,mk(t+1))。
- 迭代停止:若迭代收敛或满足停止条件,输出C∗=C(t);否则,令t=t+1,返回上一步。
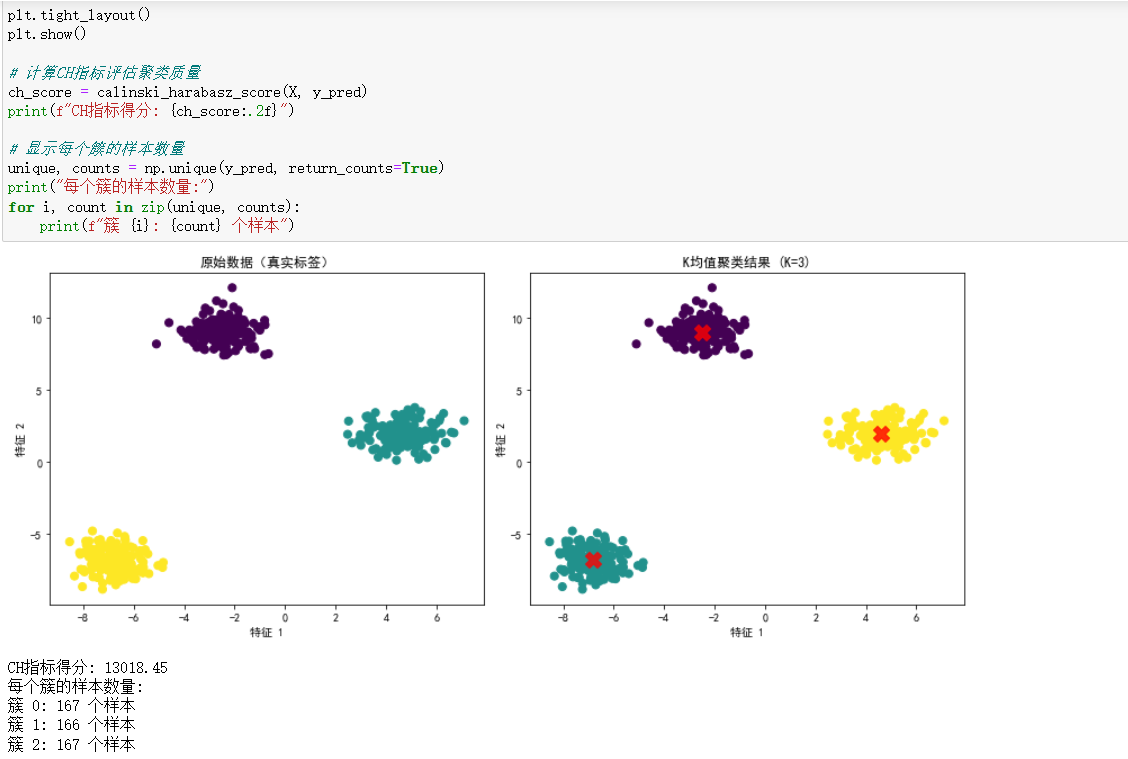
- 算法评估 - CH 指标
- 通过计算类中各点与类中心的距离平方和度量类内紧密度。
- 通过计算各类中心点与数据集中心点距离平方和度量数据集分离度。
- CH 值越大,表明类自身越紧密、类与类之间越分散,聚类结果越优。
- 优缺点
- 优点:简单快速,适合常规数据集。
- 缺点:K 值难以确定;复杂度与样本呈线性关系;很难发现任意形状的簇。
四、代码实现相关
- make_blobs():用于生成聚类数据集,参数说明如下:
参数 说明 n_samples 数据样本点个数,默认值 100 n_features 每个样本的特征数(数据维度),默认值 2 centers 类别数(标签种类数),默认值 3 cluster_std 每个类别的方差 center_box 中心确定之后的数据边界,默认值 (-10.0, 10.0) shuffle 是否将数据打乱,默认值 True random_state 随机生成器的种子,可固定生成的数据 - KMeans():用于对数据集进行 k 均值聚类,主要参数包括:
- n_cluster:分类簇的数量。
- max_iter:最大的迭代次数。
- n_init:算法的运行次数。
- random_state:随机数生成器的种子。
3.from sklearn.datasets import make_blobs make_blobs():为聚类产生数据集。
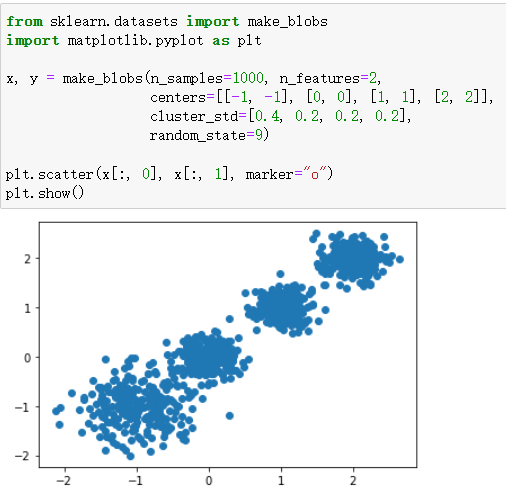
4.KMeans():使用k均值算法对数据集进行聚类。
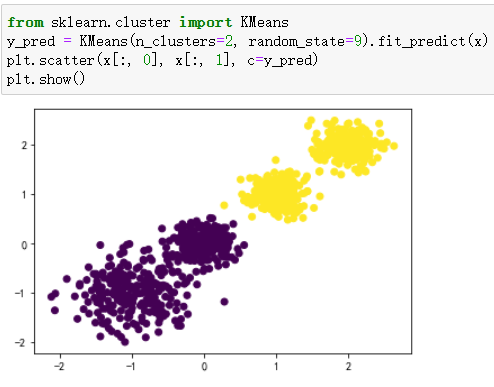
五、课堂练习
使用 make_blobs () 创建数据集,然后对其进行 k 均值聚类。