2025年8月新算法—云漂移优化算法（Cloud Drift Optimization Algorithm, CDO）

1、简介

这项研究介绍了云漂移优化（数位长）算法，这是一种创新的自然启发的元启发式方法来解决复杂的优化问题。CDO模仿受大气力影响的云粒子的动态行为，在探索和利用之间取得了微妙的平衡。它具有自适应权重调整机制，可以改变云的实时漂移行为，从而在搜索空间中进行高效导航。使用基于云的漂移策略，数位长利用概率运动更有效地在优化环境中机动。该算法经过了各种既定的单峰和多模态基准函数的严格测试，与当代顶级优化技术相比，它展示了卓越的性能，具有更快的收敛速度、高鲁棒性和卓越的解算精度。

2、算法

云是大气中的动态形成，由悬浮在空气中的水滴或冰晶组成。它们在地球的天气模式和气候调节中至关重要。云的生命周期和运动是受各种气象因素影响的复杂过程。尽管云经常被单独观察到，但它们也可以形成跨越大地理区域的庞大系统，在大陆范围内影响天气条件。云运动的独特之处在于它对不同大气条件的适应性。在其初始阶段，云形成缓慢，并在当地天气模式的影响下逐渐移动。随着它们的成熟和规模的增长，云可以在强风和压力梯度的驱动下表现出快速和不可预测的运动。
这种行为允许云长距离旅行，影响跨区域的天气状况。云运动的主要特征之一是它能够为生长和发展寻求有利的大气条件。云自然地向含水量较高、温度梯度适宜的地区吸引，这为它们的形成和持续提供了必要的条件。这种目标寻找行为对于云在动态大气中的生存和进化至关重要。在受自然启发的算法的背景下，搜索过程在逻辑上可以分为两种倾向：探索和开发。探索鼓励搜索代理突然移动并探索新的区域，而开发则侧重于局部细化和优化。云通过其自适应运动和环境相互作用自然地执行这两个功能和目标搜索。因此，如果我们能够对这种行为进行数学建模，我们就可以基于云运动原理设计一种新的自然启发算法。虽然接下来的模拟和讨论强调了数位长算法在搜索空间内定位全局最优的有效性，但随后的部分将使用各种数学函数和三个苛刻的现实世界问题来评估算法的性能。
CDO是一种受自然启发的优化算法，基于对地球大气中云的动态行为进行严格的数学建模。与通常使用线性或固定模型的传统元启发式方法不同，数位长独特地利用了云运动的两个自然阶段——开发和探索。这两个阶段相互作用，以实现高效的搜索空间探索和智能收敛以获得最佳解决方案。在该算法中，每个搜索代理（人造云）根据其相对于其他代理的性能获得动态权重，类似于大气中较重和更活跃的云如何对周围云的方向产生更大的影响。
此外，为了防止过早收敛，使用递减概率因子对云中的随机运动和意外扰动（如天气突变）进行数位长模拟。所有这些步骤都被设计成一个全面而连贯的过程，包括：随机初始化、动态加权、双峰位置更新（沉浸/探索）、自适应随机扰动和智能收敛条件。

2.1 问题定义

给定一个优化问题，其目标是最小化（或最大化）目标函数 $f(x)$在有界搜索空间 $\Omega$内，目标是找到：

$$\underset{x\in \Omega }{\min }f(x)\text{\hspace{1em}(1)}$$

其中 Ω={x∈Rd∣lb≤xi≤ub}\Omega = \{x \in \mathbb{R}^d | lb \leq x_i \leq ub\}Ω={x∈Rd∣lb≤xi​≤ub}，$lb$和 $ub$分别是解的第 $i$维的下界和上界。

2.2 初始化

算法以 $N$个候选解（云）在搜索空间内的随机初始化开始，确保对整个空间的无偏探索：

Xi0=lb+(ub−lb)⋅U(0,1),∀i∈{1,2,…,N}(2) X_i^0 = lb + (ub - lb) \cdot U(0, 1), \quad \forall i \in \{1, 2, \ldots, N\} \tag{2} Xi0​=lb+(ub−lb)⋅U(0,1),∀i∈{1,2,…,N}(2)

其中 $U(0,1)$表示在范围 [0, 1] 上的均匀随机分布。此步骤模拟了天空中云粒子的随机初始分布，其中初始位置未知且分散。

2.3 权重自适应

每个云（或粒子）根据其相对于群体中其他粒子的适应度值被分配一个动态权重。这权重决定了粒子受其他粒子位置影响的程度。每个云的权重基于适应度函数更新：

$$w_{i,j}=\{\begin{array}{ll}1+(0.3+0.7\cdot U(0,1))\cdot {\log }_{10}\left(\frac{f^{\ast }-X_i(j)}{f^{\ast }-f_{\max }}+1\right),& \text{if }i\le \frac{N}{2}\\ 1-(0.3+0.7\cdot U(0,1))\cdot {\log }_{10}\left(\frac{X_i(j)-f^{\ast }}{S}+1\right),& \text{otherwise}\end{array}\text{\hspace{1em}(3)}$$

其中 $f^{\ast }$是迄今为止找到的最佳适应度值，$S=f^{\ast }-f_{\max }+\epsilon$，其中 $\epsilon$是一个小值以避免除以零。这种权重自适应允许算法关注适应度较低的粒子，允许适应度较低的粒子探索新区域。适应性权重更新公式中的值0.3和0.7是基于广泛的经验调整确定的。它们使得缩放因子在 [0.3, 1.0] 范围内可控变化，确保有效多样性的同时自适应平衡探索和开发动态。

这种方法复制了云的自然行为，其中主要大气力影响附近粒子。在数学术语中，这类似于进化算法中常见的适应度比例选择方法。通过不断修改权重，CDQ防止早期收敛并继续有效探索，即使在后期阶段。

2.4 位置更新

每个云的位置通过探索和开发行为的组合迭代更新，决定每个云的位置。

2.4.1 开发阶段：局部细化

在此阶段，云向迄今为止找到的最佳解（即全局最佳位置）移动。位置更新方程为：

$$X_i^{(t+1)}(j)=X^{\ast }(j)+0.8\cdot v_b(j)\cdot (w_{i,j}\cdot X_A(j)-X_B(j))\text{\hspace{1em}(4)}$$

其中 $X^{\ast }(j)$是迭代 $t$时的最佳已知解。$v_b(j)\sim U(-0.2a,0.2a)$表示受因子 $a=\text{atanh}(-t/T+1)$影响的小随机调整，控制开发程度。这种细化行为模拟了云在初始运动后如何逐渐细化其形状，根据最佳附近解调整其位置。

2.4.2 探索阶段：全局搜索

在探索阶段，算法通过允许云在搜索空间内随机移动来确保搜索的多样性：

$$X_i^{(t+1)}(j)=v_c(j)\cdot X_i(j)\text{\hspace{1em}(5)}$$

其中 $v_c(j)\sim U(-0.2b,0.2b)$是另一个影响粒子运动的随机因子，其参数随时间递减，使算法从探索转向开发。

2.5 随机扰动

一些云可能会随机重新初始化，以防止过早收敛并引入算法后期阶段的探索。这以概率 $z$发生，随着算法的进展而减小：

$$X_i(j)=lb+(ub-lb)U(0,1),\text{with probability }z=0.002+0.003\cdot \left(1-\frac{t}{T}\right)\text{\hspace{1em}(6)}$$

这种随机化模拟了大气条件中不可预测的变化，可以改变漂移云的路径，确保搜索即使在最后阶段也能继续。这种技术类似于遗传算法中的模拟退火或变异算子。它模拟了突然的天气变化，使漂移的云重新定向，确保即使在后期阶段也能继续探索。通过引入偶尔的大扰动，算法保持了有效逃离局部最优并细化全局解的能力。

2.6 收敛：全局最优

当最佳解的适应度值达到预定阈值 $\epsilon$或达到最大迭代次数 $T$时，算法收敛：

$$\text{Stop if }{f}^{\ast }\le \epsilon \text{ or }t=T\text{\hspace{1em}(7)}$$

在最后阶段，搜索更加本地化，因为云收敛于全局最优，类似于云形成稳定的静止模式。CDQ算法的整体流程可以总结如下：

• 初始化：在搜索空间内随机初始化 $N$个云。
• 权重自适应：根据两个阶段更新权重。
• 探索和开发：根据两个阶段更新位置。
• 随机扰动：引入随机重新初始化以避免过早收敛。
• 收敛检查：当适应度达到迭代限制的阈值时停止。

动态权重调整、概率两阶段搜索方法和随机重新初始化的整合有助于算法可靠地收敛于全局最优。非线性控制函数（如 $\text{atanh}$和 $\tanh$）的引入促进了探索和开发阶段之间的平稳过渡。这些函数使算法能够在搜索强度上自适应地管理，而无需突然改变参数，从而实现稳定的收敛行为。云漂移优化（CDO）算法模拟了云的自然行为，通过探索和开发优化云。运动的数学建模，结合自适应行为（如权重调整和随机扰动），使算法能够避免局部最优并收敛于各种优化问题的全局解。图1展示了云和目标之间的基本相互作用和校正行为。

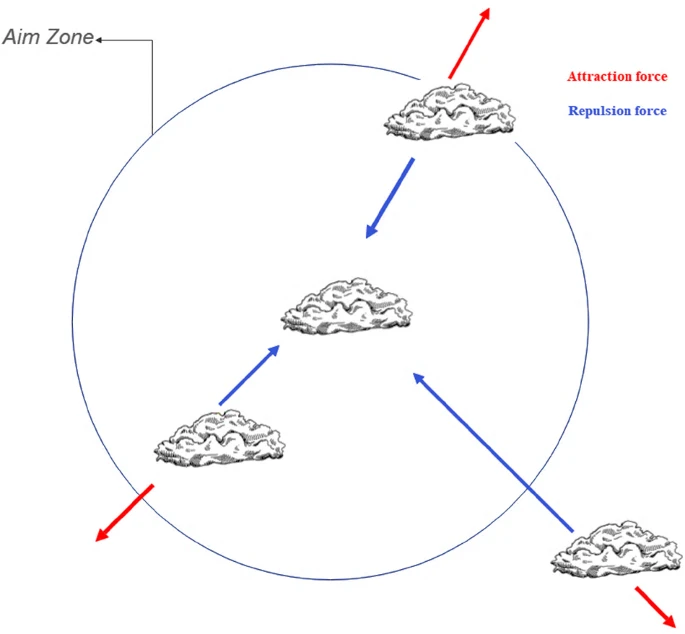
图1展示了云群中的基本相互作用和校正行为。它强调了三个关键力：吸引力：云在一定距离内相互吸引，鼓励它们更接近。排斥力：当云太接近时，排斥力将它们推开，防止重叠并确保有效的搜索空间探索。目标区域：“这代表目标区域，这些力帮助引导云朝向这个最优区域。吸引力和排斥力之间的相互作用帮助引导云朝向这个最优区域。图2展示了这些力如何平衡探索（搜索新区域）和开发（专注于有希望的区域），使群体能够有效地找到最佳解决方案。图2展示了使用该方程在2D空间中20个人工云的行为。在图中，20个人工云被要求在10次迭代中找到全局最优解。

function [Best_fitness, Best_position, Convergence_curve] = CDO(N, Max_iter, lb, ub, dim, fobj)% InitializationBest_position = zeros(1, dim);Best_fitness = inf;AllFitness = inf * ones(N, 1);weight = ones(N, dim);X = initialization(N, dim, ub, lb);Convergence_curve = zeros(1, Max_iter);it = 1;search_history = X;% Algorithm parametersz = 0.005;  % Initial probability of random movementStoppingThreshold = 1e-300;  % Lower stopping threshold for higher precisionwhile it <= Max_iter% Evaluate objective function for each solutionfor i = 1:NX(i, :) = min(max(X(i, :), lb), ub);  % Keep solutions within boundsAllFitness(i) = fobj(X(i, :));end% Sort solutions based on fitness values[SmellOrder, SmellIndex] = sort(AllFitness);bestFitness = SmellOrder(1);worstFitness = SmellOrder(N);S = bestFitness - worstFitness + eps;% Update weights dynamicallyfor i = 1:Nfor j = 1:dimif i <= (N / 2)weight(SmellIndex(i), j) = 1 + (0.3 + 0.7 * rand()) * log10((bestFitness - SmellOrder(i)) / S + 1);elseweight(SmellIndex(i), j) = 1 - (0.3 + 0.7 * rand()) * log10((SmellOrder(i) - bestFitness) / S + 1);endendend% Update the best solution found so farif bestFitness < Best_fitnessBest_position = X(SmellIndex(1), :);Best_fitness = bestFitness;end% Stop early if precision target is reachedif Best_fitness < StoppingThresholddisp(['Converged at iteration ', num2str(it)]);break;end% Adjust control parameters dynamicallya = atanh(-it / Max_iter + 1);b = 1 - it / Max_iter;z = 0.002 + 0.003 * (1 - it / Max_iter);  % Reduce random jumps over iterations% Update particle positionsfor i = 1:Nif rand < z% Random reinitialization of some solutionsX(i, :) = min(max((ub - lb) .* rand(1, dim) + lb, lb), ub);elsep = tanh(abs(AllFitness(i) - Best_fitness));vb = unifrnd(-0.2 * a, 0.2 * a, 1, dim);vc = unifrnd(-0.2 * b, 0.2 * b, 1, dim);for j = 1:dimr = rand();A = randi([1, N]);B = randi([1, N]);if r < p% Exploitation phaseX(i, j) = Best_position(j) + 0.8 * vb(j) * (weight(i, j) * X(A, j) - X(B, j));else% Exploration phaseX(i, j) = vc(j) * X(i, j);end% Fine-tuning in the final iterationsif it > 0.9 * Max_iterX(i, j) = X(i, j) * (1 - 1e-12 * randn());endendendX(i, :) = min(max(X(i, :), lb), ub);end% Store convergence dataConvergence_curve(it) = Best_fitness;it = it + 1;end
end

Alibabaei Shahraki, M. Cloud drift optimization algorithm as a nature-inspired metaheuristic. Discov Computing 28, 173 (2025). https://doi.org/10.1007/s10791-025-09671-6