SLAM文献之-Globally Consistent and Tightly Coupled 3D LiDAR Inertial Mapping

一、简介

该论《Globally Consistent and Tightly Coupled 3D LiDAR Inertial Mapping》是日本先进工业科学技术研究所（AIST）的Koide等人于2022年在IEEE国际机器人与自动化会议（ICRA）上发表的一篇论文。该研究提出了一种基于全局匹配代价最小化和LiDAR-IMU紧耦合的实时三维建图框架，旨在提高在特征稀缺或动态环境中的定位与建图精度。
文由 Koide 等人在 2022 年发表，提出了一种全局一致且紧耦合的三维 LiDAR-IMU 建图方法。其核心目标是提升在特征稀缺或动态环境下的三维定位与建图精度，并保持实时性。与传统基于位姿图优化的方法不同，本文方法直接最小化全局匹配代价，并在前端和后端紧耦合 LiDAR 与 IMU 数据，实现全局一致性和高鲁棒性。

---

二、文章贡献（创新点）

1. 全局匹配代价最小化：不依赖传统位姿图优化，直接优化全局匹配代价以保证地图全局一致性。
2. LiDAR-IMU 紧耦合：前端和后端均融合 IMU 数据，增强系统在特征稀缺环境下的鲁棒性和精度。
3. GPU 加速体素化 GICP 匹配：利用 GPU 提升匹配代价计算速度，实现实时建图。
4. 适应特征稀缺环境：可在缺乏明显几何特征的环境中仍保持高精度定位和地图生成。

---

三、详细内容

1. 算法背景

• 传统方法问题：基于位姿图优化的 LiDAR-SLAM 在特征丰富环境中表现良好，但在特征稀缺或动态环境中容易漂移。
• LiDAR-IMU 融合：通过将 IMU 数据引入前端与后端优化，提供额外约束，减少漂移，提高精度。
• 全局一致性需求：单纯局部优化容易累积误差，影响整体地图质量。

---

2. 需解决的关键问题

1. 特征稀缺环境下定位漂移：在空旷或重复结构场景中，LiDAR 匹配不稳定。
2. 高效融合 LiDAR 与 IMU 数据：前端与后端均需充分利用 IMU 信息，同时保证计算效率。
3. 实时性与计算效率：全局优化和匹配代价计算需高效以支持实时运行。

---

3. 算法流程

1. 预处理

   • 点云去畸变、滤波、体素化。

2. 前端估计

   • 关键帧选择 + 固定滞后平滑（Fixed-Lag Smoother）
   • GPU 加速的体素化 GICP 匹配代价因子
   • IMU 预积分因子约束

3. 局部建图

   • 构建局部因子图
   • 优化局部匹配代价 + IMU 约束

4. 全局建图

   • 构建全局因子图
   • 最小化全局匹配代价，保证全局一致性

---

4. 具体实现步骤

图 1 展示了提出的整体框架。整个系统由一个预处理模块和三个估计模块组成：里程计估计、本地建图和全局建图。这些模块都基于紧耦合的 LiDAR-IMU 融合。里程计估计模块（即前端）负责鲁棒地追踪传感器的运动，并提供最新状态的初始估计。随后，本地建图模块会进一步优化这些状态，并将若干局部帧整合成一个子图。全局建图模块则对这些子图的位姿进行整体优化，以确保地图全局一致性。整个流程通过多线程并行运行，提高效率。

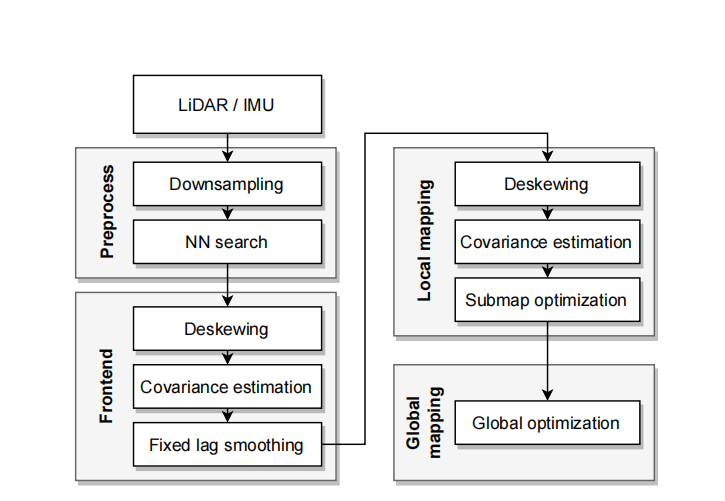
图1

用 $x\_t$ 来表示需要估计的传感器状态：

$$x_t=[T_t,v_t,b_t{]}^T,$$

其中 KaTeX parse error: Undefined control sequence: \[ at position 8: T\_t = \̲[̲R\_t | t\_t] \i… 表示位姿，$v\_t\in {\mathbb{R}}^3$ 为速度，KaTeX parse error: Undefined control sequence: \[ at position 8: b\_t = \̲[̲b^a\_t, b^\omeg… 是 IMU 的加速度和角速度偏置。状态估计依赖 LiDAR 点云 $P\_t$ 以及 IMU 测量（线加速度 $a\_t$ 和角速度 $\omega \_t$）。为了简化处理， 将 LiDAR 点云统一映射到 IMU 坐标系下。

接下来，将介绍两个核心因子：LiDAR 匹配代价因子和 IMU 预积分因子，这些因子是框架中因子图的主要组成部分，然后再详细说明每个模块的实现。

---

4.1、 LiDAR 匹配代价因子

匹配代价因子用来约束两个位姿 $T\_i$ 和 $T\_j$，目标是让它们对应的点云 $P\_i$ 和 $P\_j$ 尽可能对齐。采用体素化 GICP（Voxelized GICP, VGICP）作为代价函数，它是 GICP 的一种变体，适合 GPU 加速计算。

VGICP 会将每个点 $p\_k\in P\_i$ 用高斯分布 $(\mu \_k,C\_k)$ 来建模，其中协方差 $C\_k$ 由邻域点计算得到。点云 $P\_j$ 则被离散为体素，并为每个体素计算均值和协方差。匹配代价定义为：

$$e_M(P_i,P_j,T_i,T_j)=\sum _{p_k\in P_i}{e}_{D2D}(p_k,T_i^{-1}{T}_j),$$

$$e_{D2D}(p_k,T_{ij})=d_k^T(C_k^0+T_{ij}{C}_k{T}_{ij}^T{)}^{-1}{d}_k,$$

其中 $d\_k=\mu \_k^0-T\_ij\mu \_k$ 是点间残差，$p\_k^0=(\mu \_k^0,C\_k^0)$ 来自 $P\_j$ 的体素地图。

每次优化迭代都会重新计算并线性化 $e_M$，相比传统的 SE(3) 相对位姿约束，VGICP 提供了更精确的约束信息。

---

4.2、 IMU 预积分因子

IMU 预积分因子能够高效地将 IMU 测量融入因子图。给定加速度 $a\_t$ 和角速度 $\omega \_t$，传感器状态随时间演化：

$$R_{t+\Delta t}=R_t\exp (({\omega }_t-b_{\omega }^t-{\eta }_{\omega }^t)\Delta t),$$

$$v_{t+\Delta t}=v_t+g\Delta t+R_t(a_t-b_a^t-{\eta }_a^t)\Delta t,$$

$$t_{t+\Delta t}=t_t+v_t\Delta t+\frac{1}{2}g\Delta t^2+\frac{1}{2}{R}_t(a_t-b_a^t-{\eta }_a^t)\Delta t^2.$$

通过预积分，可以在两个时间步 $i$ 和 $j$ 之间获得相对运动约束，从而在缺乏几何特征或 LiDAR 因子受限的环境中仍能保持稳定估计，并减少四自由度漂移，同时提供重力方向约束。

---

4.3、 预处理

输入点云先经过体素滤波下采样。在去畸变过程中，每个体素不仅对点位置取平均，也对时间戳取平均。如果点的时间与体素时间差过大，会将其重新分配到新体素，以避免扫描首尾点被错误融合。

接着，为每个点找到 $k$ 个邻近点，用于协方差估计。假设去畸变过程中点的邻域关系不会发生大的变化，这些邻近点可直接用于后续计算。

---

4.4、 里程计估计

里程计估计模块通过融合 LiDAR 和 IMU 测量，补偿快速传感器运动并稳健地估计传感器状态。首先，根据 IMU 动力学预测，将点云变换到 IMU 坐标系，以去除运动畸变。随后，通过预先计算的邻近点协方差，为每个点建立不确定性模型。

在去畸变后的点云基础上，构建因子图（如图 2 所示）。为了保持实时性能，采用固定时滞平滑（fixed-lag smoothing）方法，并对旧帧进行边缘化。借鉴直接稀疏里程计（Direct Sparse Odometry）的思路，引入关键帧机制来实现高效且低漂移的轨迹估计。关键帧是一组在空间上分布合理、且与最新帧重叠度较高的帧。在最新帧与每个关键帧之间添加匹配代价因子，以减小漂移。若关键帧已被固定时滞平滑器边缘化，则其位姿被视为固定，并通过一元匹配代价因子约束最新帧的位姿。

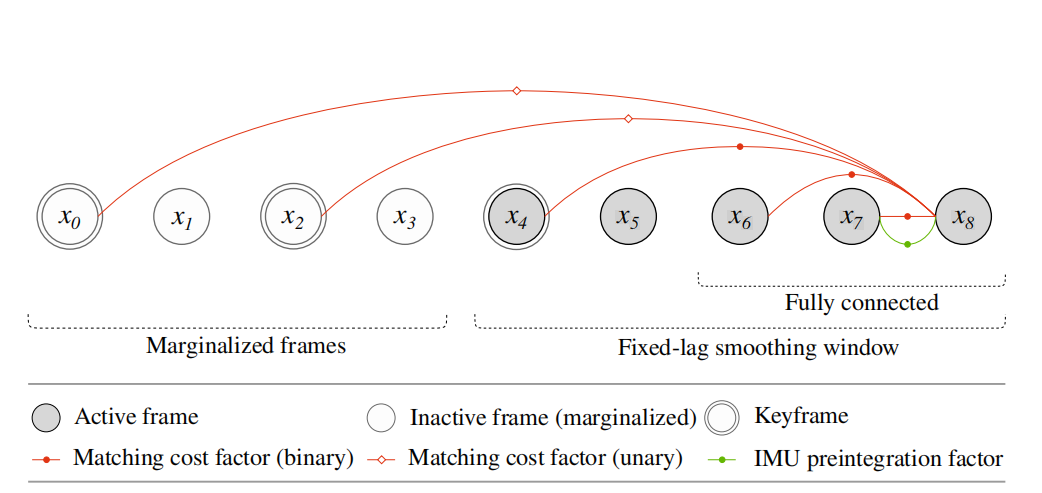
图2

关键帧管理策略如下：

1. 定义两帧 $P\_i$ 和 $P\_j$ 的重叠率为 $P\_i$ 中落在 $P\_j$ 体素内的点占比 。

2. 新帧到达时，若其与最新关键帧重叠率低于阈值（如 90%），则将其加入关键帧列表。

3. 为避免冗余关键帧：

   • 移除与最新关键帧重叠率低于阈值（如 5%）的关键帧；

   • 若关键帧总数超过 $N\_\text{odom}$（如 20），则移除评分最低的关键帧：

     s(i)=o(i,Nodom)∑j∈[1,Nodom−1]∖{i}(1−o(i,j)),s(i) = o(i, N_{\text{odom}}) \sum_{j \in [1, N_{\text{odom}}-1] \setminus \{i\}} (1 - o(i, j)), s(i)=o(i,Nodom​)j∈[1,Nodom​−1]∖{i}∑​(1−o(i,j)),

     其中 $o(i,j)$ 表示第 $i$ 帧与第 $j$ 帧关键帧的重叠率。该评分函数旨在保持关键帧在空间上的均匀分布，同时保留最新帧附近的关键帧。

此外，在最新帧与最近几帧（如最近三帧）之间建立匹配代价因子，以增强里程计对快速运动的鲁棒性。同时，连续帧之间添加 IMU 预积分因子，在特征稀少环境下进一步提升估计稳定性。

---

4.5、 局部建图

里程计估计中被边缘化的帧会被送入局部建图模块，作为子图（submap）的初始状态。局部建图将若干帧组合为子图，从而减少全局优化变量数量。

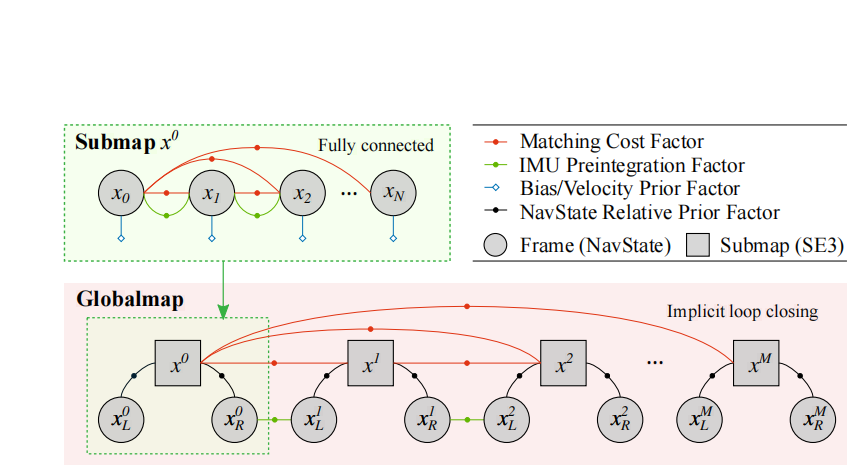
处理流程如下：

1. 使用边缘化状态重新去畸变（deskewing）并计算协方差，从而获得更准确的点云初始估计。
2. 评估新帧与子图中最新帧的重叠率，若低于阈值（如 90%），则将新帧加入子图因子图。
3. 为子图内每一帧组合添加匹配代价因子，实现全帧两两配准。
4. 连续帧间添加 IMU 预积分因子，并为每帧速度与偏置添加边缘化状态先验因子，以增强子图优化的稳定性。

当子图帧数达到 $N\_\text{sub}$（如 15）或首尾帧重叠率低于阈值（如 5%）时，通过 Levenberg-Marquardt 优化器 对因子图进行优化，并将优化结果合并为单个子图。

---

4.6、 全局建图

全局建图模块用于消除累积漂移，实现全局一致的地图构建。每对子图间若重叠率超过阈值（如 5%），则创建匹配代价因子，生成稠密的全局因子图。这样，子图不仅与相邻子图对齐，还能与重新访问的子图对齐，从而实现闭环校正。

由于子图创建间隔较大（如 10 秒），仅依赖 IMU 因子无法有效约束子图间相对位姿，同时会丢失局部建图的速度与偏差信息。为解决这一问题， 为每个子图 $x\_i$ 引入两个“端点”状态：$x\_i^L$ 和 $x\_i^R$，分别对应子图首尾帧相对于子图原点的状态。

具体做法：

1. 子图原点 $T\_i$ 定义为中间帧 $T\_N\_\text{sub}/2$ 的位姿。
2. 将每帧状态 $x\_t$ 表示为相对于子图原点的状态。
3. 在 $x\_i$ 与端点 $x\_i^L,x\_i^R$ 之间创建相对状态因子，以满足公式 11–13。
4. 在$x\_i^R$ 与 $x\_{i+1}^L$ 之间添加 IMU 因子，以覆盖较短时间间隔，既约束子图位姿，又保留局部建图速度与偏差信息。

每当累积若干新子图（如每 5 个）时，使用 GTSAM 的 iSAM2 优化器对全局因子图进行增量优化，持续更新全局一致的地图。

---

四、优势总结

1. 全局一致性：通过全局匹配代价最小化保证地图一致性。
2. 高鲁棒性：紧耦合 LiDAR-IMU，可在特征稀缺或动态环境中保持精度。
3. 实时性：GPU 加速匹配代价计算，前端/后端优化高效。
4. 灵活扩展：方法可适应不同传感器速率、不同点云密度和环境类型。

---

五、参考文献

1. Koide, K., Yokozuka, M., Oishi, S., & Banno, A. (2022). Globally Consistent and Tightly Coupled 3D LiDAR Inertial Mapping. IEEE ICRA 2022. PDF
2. Koide, K., Yokozuka, M., Oishi, S., & Banno, A. (2021). Globally Consistent 3D LiDAR Mapping with GPU-accelerated GICP Matching Cost Factors. IEEE Robotics and Automation Letters, 6(3), 5282–5289.
3. Shan, T., Englot, B., Meyers, D., Wang, W., Ratti, C., & Rus, D. (2020). LIO-SAM: Tightly-coupled Lidar Inertial Odometry via Smoothing and Mapping. arXiv:2007.00258.

---

相关文献