117. 软件构建,拓扑排序,47. 参加科学大会,dijkstra算法
117. 软件构建
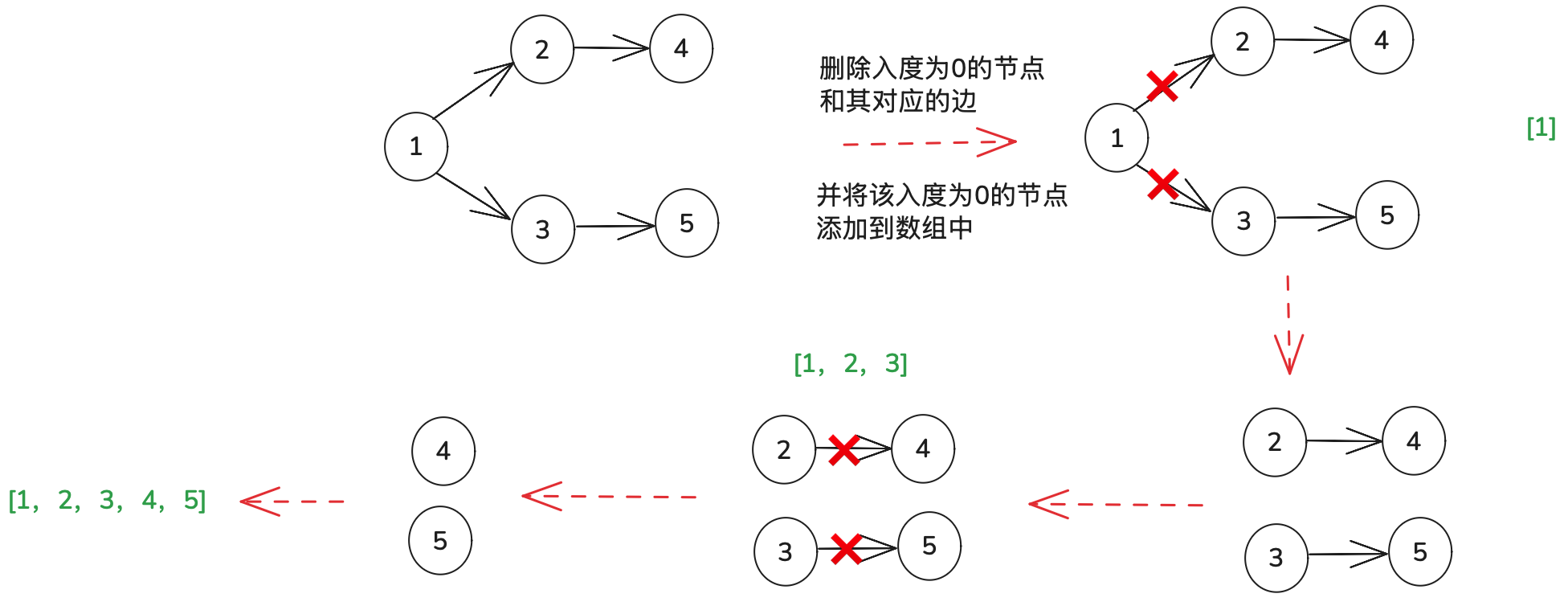
拓扑排序
思路:
- 找到入度为0的节点,并添加到result数组中
- 将该节点从图中移除,并删除其相连的边
- 重复执行这个过程
- 如果result数组的长度 == 图的节点数目,则证明这个图的所有节点可以构成一颗树;否则,则证明图中存在环路。

拓扑排序广搜Code
## 如果能全部处理后所有文件,则输出处理文件的路径(非唯一)。
## 即判断这个图的所有节点能否构成一颗树from collections import deque, defaultdictif __name__ == "__main__":document_size, edge_size = map(int, input().split())graph = [[0]*document_size for _ in range(document_size)]in_edge = [0] * document_size ## 初始化一个入度数组result = []umap = defaultdict(list) ## 存储文件的依赖关系。一个字典,key是int, value是listqueue = deque() ## 存储入度为0的节点for _ in range(edge_size):S_document, T_document = map(int, input().split())umap[S_document].append(T_document)in_edge[T_document] += 1for i in range(document_size):if in_edge[i] == 0:queue.append(i) ## 存储第一轮入度为0的节点,如果这一轮没有入度为0的节点,那么直接输出-1if len(queue) == 0:print(-1) while queue: ## 队列不为空,证明存在入度为0的节点cur_document = queue.popleft()result.append(cur_document) ## 添加此次入度为0的点for next_document in umap[cur_document]: ## 当前document指向next_document的边删除 in_edge[next_document] -= 1 ## 更新in_edgeif in_edge[next_document] == 0: ## 确保继承关系queue.append(next_document)if len(result) != document_size:print(-1)else:print(" ".join(map(str, result)))注意:
要熟悉掌握从collections packiage去使用队列deque,和字典defaultdict的方法。
umap = defaultdict(list) 在这里umap使用了defaultdict,因此是一个字典,而里面是list,则说明了该字典的value是一个数组,掌握这种方式很有利于本题去找到入度为0的点指向的下一个节点。
