决策树的学习

一、整体框架与核心定位

本 PPT 围绕机器学习中的树模型展开，核心聚焦决策树算法，系统讲解其基本概念、组成结构、训练与测试流程、关键技术（特征切分）及实际构造实例，最后辅以课堂练习巩固知识，逻辑清晰，从理论到实践逐步递进。

二、决策树基础概念

1. 核心定义：决策树是从根节点开始，通过逐步判断分支，最终走到叶子节点得出决策的模型。所有数据最终都会落到叶子节点，兼具分类和回归能力。
2. 树的组成结构

根节点：整个决策树的第一个选择点，是特征选择的起点。

非叶子节点与分支：决策过程中的中间环节，每个非叶子节点对应一个特征判断，分支则代表该特征的不同取值。

叶子节点：决策的最终结果，每个叶子节点对应一个具体的分类或回归结论。

三、决策树的训练与测试

1. 训练阶段：核心任务是从给定训练集中构造决策树。关键步骤是 “从根节点开始选择特征，并确定特征的切分方式”，这是决策树构建的难点。
2. 测试阶段：流程简单，只需将测试数据代入已构造好的决策树，从根节点到叶子节点 “走一遍”，即可得到分类或回归结果。

四、特征切分的核心：衡量标准与计算

（一）核心问题

构建决策树的关键是 “如何选择特征作为节点（如根节点、子节点）”，目标是让每个节点能 “更好地切分数据”，提升分类效果。

（二）核心衡量标准：熵

1. 熵的定义：熵是衡量随机变量不确定性的度量，公式为 H(X)=- 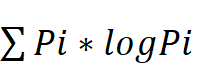(i=1,2,...,n),(pi为随机变量取第i个值的概率）。
2. 熵的规律

不确定性越大，熵值越大；不确定性越小，熵值越小。

极端情况：当(p=0)或(p=1)时，H(p)=0（随机变量完全确定，无不确定性）；当(p=0.5)时，H(p)=1（随机变量不确定性最大）。

1. 实例对比

A 集合[1,1,1,1,1,1,1,1,2,2]：数据类别集中，不确定性小，熵值较低。

B 集合[1,2,3,4,5,6,7,8,9,1]：数据类别分散，不确定性大，熵值较高。

决策树目标：通过节点分支后，使数据类别的熵值变小（降低不确定性，让同类数据更集中）。

（三）特征选择依据：信息增益

1. 定义：信息增益表示 “特征 X 使得类 Y 的不确定性减少的程度”，反映分类后的 “专一性”—— 希望分类后同类数据聚集在一起。
2. 应用逻辑：计算每个特征的信息增益，选择信息增益最大的特征作为当前节点（如根节点选信息增益最大的特征，子节点再从剩余特征中选信息增益最大的，以此类推）。

五、决策树构造实例

（一）实例背景

数据：14 天的打球情况记录（9 天打球，5 天不打球）。

特征：4 种环境特征（outlook / 天气、temperature / 温度、humidity / 湿度、windy / 是否有风）。

目标：基于数据和特征构造决策树，判断 “是否适合打球”。

（二）构造步骤（以 outlook 特征为例）

1. 计算初始熵：14 天中 9 天打球（概率 9/14）、5 天不打球（概率 5/14），初始熵值为 0.940。
2. 按 outlook 特征划分并计算各分支熵

outlook=sunny：对应数据的熵值为 0.971。

outlook=overcast：对应数据全为 “打球”，熵值为 0。

outlook=rainy：对应数据的熵值为 0.971。

1. 计算 outlook 特征的条件熵：根据各分支概率加权求和，即514*0.971+414*0+514*0.971=0.693。
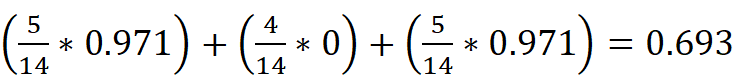2. 计算信息增益：初始熵 - 条件熵 = 0.940 - 0.693 = 0.247。
3. 特征选择：用同样方法计算 temperature、humidity、windy 的信息增益，选择信息增益最大的特征作为根节点；后续子节点再从剩余特征中重复此过程，逐步构建完整决策树。

六、课堂练习

提供 “判断生物是否属于鱼类” 的数据集，包含 2 个特征（不浮出水面是否可以生存、是否有脚蹼）和 5 条数据，要求学员基于所学方法构造决策树，巩固特征选择、熵与信息增益计算等核心知识点。