——分治——
目录
1 颜色分类
2 排序数组 (快排)
3 数组中的第K个最大元素 (快速选择算法)
4 库存管理 III
5 排序数组(归并)
6 交易逆序对的总数
7 计算右侧小于当前元素的个数
8 翻转对
分治顾名思义就是分而治之,我们将一个大问题转换为若干了相同或者相似的子问题,然后将子问题再继续转换为更小的子问题,直到划分足够小,能够快速得出结果。比如我们的快排,他其实就是在一个区间内将数据以key划分为两个子区间,然后在子区间中继续去执行快排的策略,直到只有一个或者没有数据的时候就返回。同时归并排序也是类似的,但是归并排序是先对子区间进行排序,然后在进行归并的操作。
对于传统的快排,其实有一些缺陷,比如当区间中存在多个与key相等的元素时,传统快排的思想是将这些重复的key都放在左子区间或者全部放在右子区间,而后还需要在子区间中进行排序,但是其实我们完全可以将整个数组划分为三个区间, 小于key 的左区间,全部为key的区间以及大于key的右区间,这样一来,中间的key的区间并不需要再去子区间进行排序,在很多时候可以减少子区间排序的数据量。那么具体怎么划分为三个区间呢?我们会先从颜色划分入手,了解如何进行区间划分。
1 颜色分类
75. 颜色分类 - 力扣(LeetCode)

题目解析:给定一个颜色数组,将数组进行排序,使得相同元素相邻,同时数组整体按照红色、白色、蓝色进行排列。 而由于红、白、蓝分别是0,1,2,其实就相当于让我们将数组排序。
最偷懒的做法当前就是调用sort进行排序,但是我们可以有更优秀的算法,也叫三色划分,可以将数组按照性质划分为三个区间。
三色划分的本质其实就类似于双指针的移动零的题目,只不过在移动零中,只有两个指针,只能将已遍历的区间划分为两部分,而我们只需要再加一个指针,就能够将已遍历的区间划分为三个区间。
我们使用 left ,right 来对已遍历的区间进行划分, i 来进行数组的遍历。
那么我们可以维护 [0,left]为 红色的区间,(left,right]为白色区间,(right,i]为蓝色区间。
那么遍历过程中,nums[i]有三种情况:
1、蓝色,那么此时不需要移动指针;
2、白色,此时需要将白色区间扩大,同时蓝色区间右移,我们可以将蓝色区间的第一个元素与nums[i]交换,然后 ++right就可以了。
3、红色,此时红色区间需要扩大,蓝色和白色区间需要右移,此时我们先将nums[i]与nums[++right] 进行交换,先将蓝色区间右移,此时白色区间也相当于扩大了,然后再swap(nums[++left],swap[righjt] ,将白色区间右移以及扩大红色区间。
代码如下:
class Solution {
public:void sortColors(vector<int>& nums) {int left = -1 , right = -1 , n = nums.size();for(int i = 0 ; i < n ; ++i){if(nums[i] == 2) continue;else if(nums[i] == 1){swap(nums[i] , nums[++right]);}else {swap(nums[i] , nums[++right]);swap(nums[++left] , nums[right]);}}}
};
2 排序数组 (快排)
912. 排序数组 - 力扣(LeetCode)

本题我们使用快排对数组进行排序,根据上面所使用的三色划分的算法原理,我们可以将区间划分为三个子区间,小于key的,等于key的,大于key的,这样一来,后续只需要再去排序小于key和大于key的区间就行了,而不需要再处理等于key的区间,相较于传统的快排还是有一些效率的提升的。
代码如下:
class Solution {
public:void _sort(vector<int> & nums, int begin , int end){if(begin >= end) return;int index = begin + random() % (end - begin + 1); //随机选key//然后开始三色划分int left = begin - 1 , right = begin - 1 , key = nums[index];for(int i = begin ; i <= end ; ++i){if(nums[i] > key) continue;else if(nums[i] == key){swap(nums[++right] , nums[i]);}else{swap(nums[i] , nums[++right]);swap(nums[++left] , nums[right]);}}_sort(nums,begin,left); //小于key的区间[begin, left]_sort(nums,right+1,end); //大于key的区间(right,end]}vector<int> sortArray(vector<int>& nums) {srand(time(nullptr));//采用随机取key_sort(nums,0,nums.size()-1);return nums;}
}; 
3 数组中的第K个最大元素 (快速选择算法)
215. 数组中的第K个最大元素 - 力扣(LeetCode)

题目解析:本题是一个topK问题,常规解法就是使用固定大小的堆来处理。
在本题我们会给予快排的思想,使用快速选择算法来解决topK问题。
我们要在nums中求第 K 大的元素,那么当我们对nums进行一次三色划分之后,假设三个区间的大小分别为 a , b , c ,那么如果 K <= c ,说明第K大的元素在大于key的右区间中,此时我们递归去右区间找第K大的元素。 而如果 K > c && K <= b + c ,那么说明第K大的元素就在等于key的区间中,此时直接返回key就行了,而如果 K > b + c,说明第K大的元素在小于key的做区间中,此时我们要递归到左区间去找,但是在左区间找的是第 K-b-c大的元素。
代码如下:
class Solution {
public:int _sort(vector<int>& nums , int k , int begin , int end){if(begin == end) return nums[begin];int index = begin + random() % (end - begin + 1);int key = nums[begin] , left = begin - 1 , right = begin -1;for(int i = begin ; i <= end ; ++i){if(nums[i] > key) continue;else if(nums[i] == key) swap(nums[++right] , nums[i]);else{swap(nums[i],nums[++right]);swap(nums[++left],nums[right]);}}int c = end - right , b = end - left - c , a = left - begin + 1;if(k <= c) return _sort(nums,k,right + 1 ,end);else if(k <= b + c) return key;else return _sort(nums , k - b - c , begin ,begin + a -1);}int findKthLargest(vector<int>& nums, int k) {srand(time(nullptr));return _sort(nums,k,0,nums.size() - 1);}
};
本题是求第k大的数,如果是第k小的数,那么在递归子区间的时候条件换一下就行了。
4 库存管理 III
LCR 159. 库存管理 III - 力扣(LeetCode)

题目解析:本题要求我们找出stock数组的前k小的数并进行返回。
还是使用三色划分的快排的思路,当我们进行完一次三色划分之后,假设左区间数据个数为a,中减区间数据个数为b,右区间数据个数为c。
当 k < a 时,此时我们需要递归左区间找前k小的数。
当 k <= a + b时,此时我们直接将前k个数放进结果返回就行了。
当k > a + b时,此时我们需要将前a + b 个数都放进返回数组,接着递归右区间找前 k - a - b小的数。
代码如下:
class Solution {
public:void _sort(vector<int>& nums , int k , int begin , int end , vector<int>& res){if(begin == end){res.push_back(nums[begin]);return;}int index = begin + random() % (end - begin + 1) , key = nums[index];int left = begin - 1, right = begin - 1;for(int i = begin ; i <= end ; ++i){if(nums[i] > key) continue;else if(nums[i] == key) swap(nums[++right] , nums[i]);else{swap(nums[i],nums[++right]);swap(nums[++left],nums[right]);}}int a = left - begin + 1 , b = right - left , c = end - right;if(k < a) return _sort(nums , k , begin , left , res);else if(k <= a + b){for(int i = 0 ; i < k ; ++i){res.push_back(nums[begin + i]);}return;}else{for(int i = 0 ; i < a + b ; ++i){res.push_back(nums[begin + i]);}_sort(nums,k - a - b,right + 1 ,end ,res);}}vector<int> inventoryManagement(vector<int>& nums, int cnt) {vector<int> res;srand(time(nullptr));_sort(nums,cnt,0,nums.size()-1,res);return res;}
};
5 排序数组(归并)
912. 排序数组 - 力扣(LeetCode)

题目解析:本文第2题,在这里使用归并排序思路。
归并排序的思路和快排类似,都是将数组划分为两个区间,递归展开类似于二叉树的结构,但是快排是一种二叉树的前序遍历,也就是先将整个数组以key值进行划分,然后再去递归排序左右子区间,而归并则是二叉树的后序遍历,将区间划分为左右区间,先将左右子区间进行排序,然后再将排完序的左右子区间进行归并。在归并排序划分做右区间的时候,为了使得二叉树的深度也就是递归的深度尽可能少,我们一般采用平均划分区间,让左右区间长度相等或者差一,使得递归的深度最低。
而递归的结束条件就是区间只有一个元素,此时一个元素就是有序的。
归并排序的特点就是需要开辟额外空间来进行归并,存放合并之后的有序区间,然后再放回数组中。在做算法题的时候,这个额外空间我们可以使用全局的数组。
代码如下:
class Solution {
public:int tmp[50000]; void merge(vector<int>& nums , int begin , int end){if(begin >= end) return ;//先将左右子区间排序int mid = begin + (end - begin) / 2;merge(nums,begin,mid);merge(nums,mid+1,end);//对有序的左右子区间进行归并int left = begin , right = mid + 1 , i = 0;while(left <= mid && right <= end){if(nums[left] < nums[right]) tmp[i++] = nums[left++];else tmp[i++] = nums[right++];}while(left <= mid) tmp[i++] = nums[left++];while(right <= end) tmp[i++] = nums[right++];//将归并之后的数据放回原数组for(int i = 0 ; i < end - begin + 1 ; ++i)nums[begin + i] = tmp[i]; }vector<int> sortArray(vector<int>& nums) {merge(nums,0,nums.size()-1);return nums;}
};
6 交易逆序对的总数
LCR 170. 交易逆序对的总数 - 力扣(LeetCode)

题目解析:要求我们求出数组中逆序对的个数,只要满足i < j && nums[i] > nums[j] 的二元组就是一个逆序对。
暴力解法:枚举所有的 i<j 的二元组,或者说 j > i 的二元组,统计逆序对的个数,两层循环枚举i和j,时间复杂度为O(N^2)。
由于数据范围很大,所以这种暴力解法大概率会超时,我们也就不去尝试了。
对于nums[j],我们要找到nums[j]前面有多少个比nums[j]大的元素,假设我们有两个有序区间,其中,nums[j]在右区间,左区间[0,x],那么左区间中能够与nums[j]构成逆序对的个数,我们可以找到左区间的第一个nums[i] > nums[j] ,那么[i,x]区间内的所有元素都是大于nums[j]的,那么在左区间中,与nums[j]构成的逆序对的个数就是 x - i + 1个。当然右区间中也可能有能与nums[j]构成逆序对的元素,但是我们再划分更小区间的时候,他们也会和nums[j]划分为左右区间,也会被统计到。
那么我们如果把这个过程放到归并排序中,merge(nums,begin,right) ,划分出来两个区间,[begin,mid],[mid+1,end],两个元素都在左区间或者右区间中所有的逆序对,我们在递归过程中就已经统计过了,在本层我们只需要考虑右区间与左区间各一个元素构成的逆序对,其中左区间的元素一定在右区间的元素前面,那么只需要找到左区间中比右区间的元素大的二元组就行了。
我们在归并的过程中,当 nums[left] <= nums[right] ,把nums[left]放入临时空间中,但是当 nums[left] > nums[right] 时,此时说明nums[left] 比 [mid+1, right] 的元素都要大,那么nums[left]可以与[mid+1,right]的所有元素构成逆序对,我们需要做统计,但是有可能nums[left]会比nums[right]+1都还要大,那么可能会出现重复统计的情况,那么我们可以换一种方式,当nums[left]>nums[right]的时候,此时[left,mid]的所有元素都是大于nums[right]的,也就是[left,mid]的所有元素都可以与nums[right]构成逆序对,此时计数增加 mid - left + 1
要注意理解的是,在本层函数归并过程中,我们只需要考虑一个元素在左区间一个元素在右区间的逆序对的情况,其他情况其实在更小的区间的归并过程中就已经计算过了。
代码如下:
class Solution {
public:int tmp[50001];int merge(vector<int>& nums , int begin , int end){if(begin >= end) return 0;int res = 0 , mid = begin + (end - begin) / 2;//统计两个元素都在左区间的逆序对个数res += merge(nums, begin , mid);//统计两个元素都在右区间的逆序对个数res += merge(nums , mid + 1 , end);//然后统计两个元素分别在做右区间的逆序对的个数int left = begin , right = mid + 1 , i = 0;while(left <= mid && right <= end){if(nums[left] <= nums[right]) tmp[i++] = nums[left++]; //说明nums[right]无法与左区间的元素构成逆序对else{ //说明nums[left] > nums[right],那么nums[right]能够与[left,mid]的所有元素构成逆序对res += mid - left + 1;tmp[i++] = nums[right++];}}while(left <= mid){ //nums[left]比右区间所有元素都大,但是已经统计过了tmp[i++] = nums[left++];}while(right <= end){ //nums[right] 比左区间所有元素都大,对于right没有逆序对了tmp[i++] = nums[right++];}//还原到原数组for(int i = 0 ; i < end - begin + 1 ; ++i){nums[begin + i] = tmp[i];}return res;}int reversePairs(vector<int>& record) {return merge(record , 0 , record.size()-1);}
};
7 计算右侧小于当前元素的个数
315. 计算右侧小于当前元素的个数 - 力扣(LeetCode)

题目解析:本题其实也是要找逆序对的个数,但是我
class Solution {
public:int tmp[100000];//对下标数组进行归并排序void merge(const vector<int>& nums, vector<int>& index, vector<int>& res , int begin , int end){if(begin >= end) return;int mid = begin + (end - begin) / 2 ;//对两个元素都在左区间的逆序对进行统计merge(nums,index,res,begin,mid);//对两个元素都在右区间的逆序对进行统计merge(nums,index,res,mid+1,end); //对一左一右的逆序对进行统计,从后往前进行归并int left = mid , right = end , i = end - begin; //元素个数为 end - begin + 1 ,最大下标就是 end - begin//注意index[i] 代表的是 nums[index[i]]while(left >= begin && right >= mid + 1){if(nums[index[left]] > nums[index[right]]){ //说明left 能和[mid+1 ,right] 的所有元素构成逆序对 res[index[left]] += right - mid;tmp[i--] = index[left--]; }else tmp[i--] = index[right--];}while(left >= begin) tmp[i--] = index[left--]; //此时说明left比右区间所有元素都小,无需统计while(right >= mid + 1) tmp[i--] = index[right--]; //此时说明right比左区间所有元素都小,但是已经统计过//还原到原数组for(int i = 0 ; i < end - begin + 1 ; ++i){index[begin + i] = tmp[i];}}vector<int> countSmaller(vector<int>& nums) {int n = nums.size();vector<int> index(n) , res(n);for(int i = 0 ; i < n ; ++i) index[i] = i; //初始化下标数组merge(nums,index,res,0,n-1);return res;}
};们需要分别统计到每个元素的逆序对上。
暴力解法:两层循环遍历所有二元组。
本题思路和上一题一样,需要借助归并排序的思路,但是由于我们需要将逆序对{nums[i],nums[j]}计数到 count[i] 上,所以在归并过程中其实有一点需要变化,如果还是按照上一题的归并思路,当nums[left] > nums[right] 时,nums[right] 与 [left,mid]都能够构成逆序对,那么此时需要一个循环来讲count的 [left,mid] 区间都进行加一操作。我们需要将这个循环优化掉。
其实很简单,我们从前往后不好统计,那么可以从后往前找大的数进行归并。
当nums[left] > nums[right]的时候,说明nums[left] 能够和右区间的 [mid+1,right] 构成逆序对,那么count[left] += right - mid; 同时将left归并。
当nums[left] <= nums[right] 的时候,将nums[right] 归并到临时数组。
但是这样其实就诞生了一个更大的问题,因为我们归并的过程是在排序,那么nums中元素的位置其实是在发生变化的,我们当前栈帧的 nums[left] 不一定是题目给定数组的nums[left] ,那么不应该统计到count[left] ,而应该统计到该数据在数组的原位置的下标上。
遇到这种题目,一般使用的技巧就是不对数据本身进行排序,而是使用下标数组,对下标数组进行排序。
比如我们要排序: nums = [1, 3 ,5 ,4 ,7] ,我们可以初始化一个下标数组为: index=[0,1,2,3,4]
那么我们接下来其实是对index数组进行排序,但是下标数组的元素代表的是 nums[index[i]],大小关系以及排序的时候,使用的是 nums[index[i]] 来比较大小。那么排完序之后,下标数组最终为 index = [0,1,3,2,4] ,这样一来,我们其实得到的是最终排完序的数组的各个元素在原始数组的下标,就不需要担心找不到元素的原始下标了。
代码如下:
class Solution {
public:int tmp[100000];//对下标数组进行归并排序void merge(const vector<int>& nums, vector<int>& index, vector<int>& res , int begin , int end){if(begin >= end) return;int mid = begin + (end - begin) / 2 ;//对两个元素都在左区间的逆序对进行统计merge(nums,index,res,begin,mid);//对两个元素都在右区间的逆序对进行统计merge(nums,index,res,mid+1,end); //对一左一右的逆序对进行统计,从后往前进行归并int left = mid , right = end , i = end - begin; //元素个数为 end - begin + 1 ,最大下标就是 end - begin//注意index[i] 代表的是 nums[index[i]]while(left >= begin && right >= mid + 1){if(nums[index[left]] > nums[index[right]]){ //说明left 能和[mid+1 ,right] 的所有元素构成逆序对 res[index[left]] += right - mid;tmp[i--] = index[left--]; }else tmp[i--] = index[right--];}while(left >= begin) tmp[i--] = index[left--]; //此时说明left比右区间所有元素都小,无需统计while(right >= mid + 1) tmp[i--] = index[right--]; //此时说明right比左区间所有元素都小,但是已经统计过//还原到原数组for(int i = 0 ; i < end - begin + 1 ; ++i){index[begin + i] = tmp[i];}}vector<int> countSmaller(vector<int>& nums) {int n = nums.size();vector<int> index(n) , res(n);for(int i = 0 ; i < n ; ++i) index[i] = i; //初始化下标数组merge(nums,index,res,0,n-1);return res;}
};
8 翻转对
493. 翻转对 - 力扣(LeetCode)
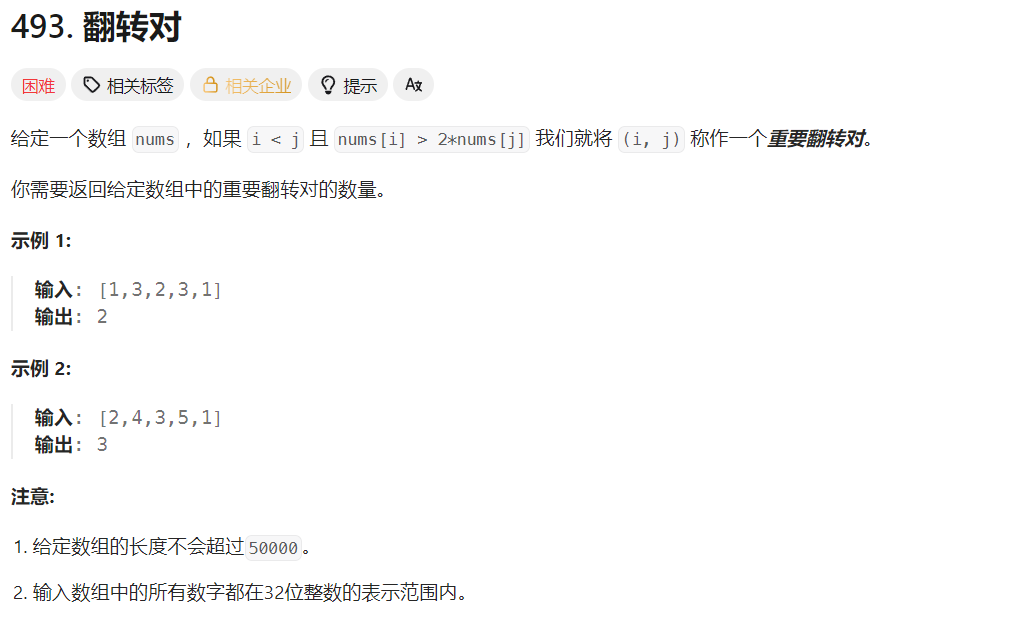
题目解析:重要翻转对的定义就是前面出现的元素比后面出现的元素的两倍都要大,要求我们统计数组的重要翻转对的数量。
暴力解法:两层循环暴力枚举,但是不用想肯定会超时。
我们还是使用归并排序的思想,在归并的过程中进行统计。由于本题我们要找的是前面的元素比后面的元素大,那么我们使用归并进行降序排序。
在排序过程中,我们本层只需要找一左一右的重要翻转对,那么对于nums[i] ,我们需要找到右区间中小于nums[i]/2 的第一个元素的位置,那么我们可以使用二分查找,其实就是一个查找右边界的问题。而每一层的二分查找我们也可以进行一定的优化,当我们找到右区间中第一个 <nums[i]/2的元素的位置的时候,假设下标为 j ,那么nusms[i+1] 是比nums[i]小的,那么对应的右区间的第一个小于nums[i+1]/2的元素下标一定是要比 j 大的,所以后续我们只需要在[j,end]中进行一次二分查找左边界就行了。
代码如下:
class Solution {
public:int tmp[50000];int merge(vector<int>& nums , int begin ,int end){if(begin >= end) return 0;int mid = begin + (end - begin)/2;int res = 0;//统计两个元素都在左区间的重要翻转对的数量res += merge(nums,begin,mid);//两个元素都在右区间res += merge(nums,mid+1,end);//先统计重要翻转对的数量int j = mid + 1; //在[j,end]区间内进行二分for(int i = begin ; i <= mid ; ++i){// int l = j , r = end;// while(l < r){// int m = (l + r) / 2 ; //数据范围不会溢出,我们直接计算就行了// if(nums[m] * 2 >= nums[i]){// l = m + 1;// }// else r = l;// }// j = l;// res += end - j + 1;//或许这里我们直接滑动更好?while( j <= end && (long long)nums[j] * 2 >= nums[i]) ++j;if(j > end) break;else res += end - j + 1;}//然后再进行归并int left = begin , right = mid + 1, i = 0 ;while(left <= mid && right <= end){if(nums[left] >= nums[right]) tmp[i++] = nums[left++]; //注意要排降序else tmp[i++] = nums[right++];}while(left <= mid) tmp[i++] = nums[left++];while(right <= end) tmp[i++] = nums[right++];for(int i = 0 ; i < end - begin + 1 ; ++i) nums[begin + i] = tmp[i];return res;}int reversePairs(vector<int>& nums) {return merge(nums,0,nums.size()-1);}
};
总结
本文主要讲解了分治的两种经典应用: 快排和归并,并使用三色标记法,优化了传统的快排,提高了效率,同时基于三色标记法的快速选择算法,可以用于解决topK问题。而归并算法的递归顺序则是一种二叉树的后续遍历,很适合处理先处理子区间有序,再处理整体有序的问题,比如文中的逆序对等问题。
