pytorch线性回归

一、直线求解与拟合

1.1 两点确定一条直线

对于直线方程可以用如下方程表示：

$$Ax+By+C=0$$

当b≠0时（也就是非垂直于x轴的直线），可以写成

$$y=-\frac{A}{B}x-\frac{C}{B}$$

如果令

$$k=-\frac{A}{B}$$

$$b=-\frac{C}{B}$$

则直线方程可以写为

$$\begin{array}{r}y=kx+b\end{array}$$

其中k也称作斜率，代表直线的倾斜程度；b则表示截距，标明了直线在y轴的位置（x = 0时，y = b），斜率和截距在后文中有重要作用。假设已知直线上两个点的坐标(x1, y1)，(x2, y2)，则可以得到如下二元一次方程组：

$$\begin{array}{r}{y}_1=k{x}_1+b\end{array}$$

$$\begin{array}{r}{y}_2=k{x}_2+b\end{array}$$

可以求解出

$$k=\frac{y_1-y_2}{x_1-x_2}$$

再把求出来的k代入(2)或者(3)中，就可以求出b值，从而得到(1)表达式表示的直线方程。

1.2 从精确求解到优化拟合

在1.1章节中，如果两点坐标是(1, 3)、(2, 5)，则可以求出直线方程为y = 2x + 1，此时数据完全精确，直线穿过所有点。

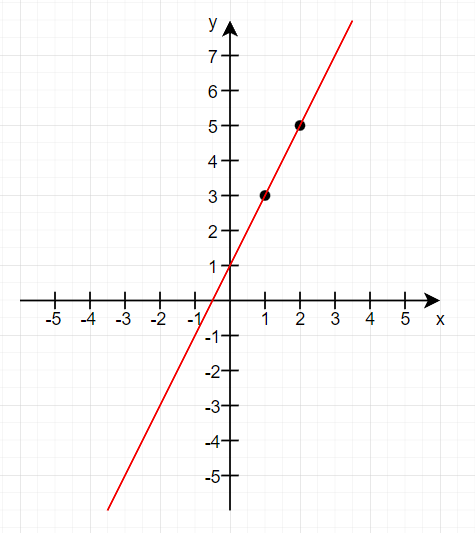
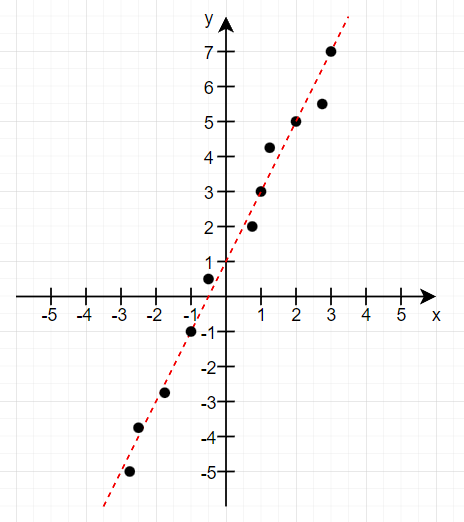
但是现实世界中，数据远远不止两个点，并且数据还会因测量误差（传感器精度限制）、环境干扰（温度、湿度变化）、人为因素（数据记录偏差）、系统噪声（电子设备白噪声）等原因导致不存在任何一条直线能穿过所有点。于是现实中更多不是对这条直线求解，而是让一条直线尽可能的 拟合 所有的点。

二、几何距离与回归残差

可以使用所有点到直线的几何距离或者残差来定义点与线的“拟合程度”，值越小拟合度越高。定义拟合度的函数叫做损失函数（Loss Function），于是问题转换成了：给定一些坐标点，求k和b，使得所给的点到直线y = kx + b的损失函数值最小。

2.1 几何距离

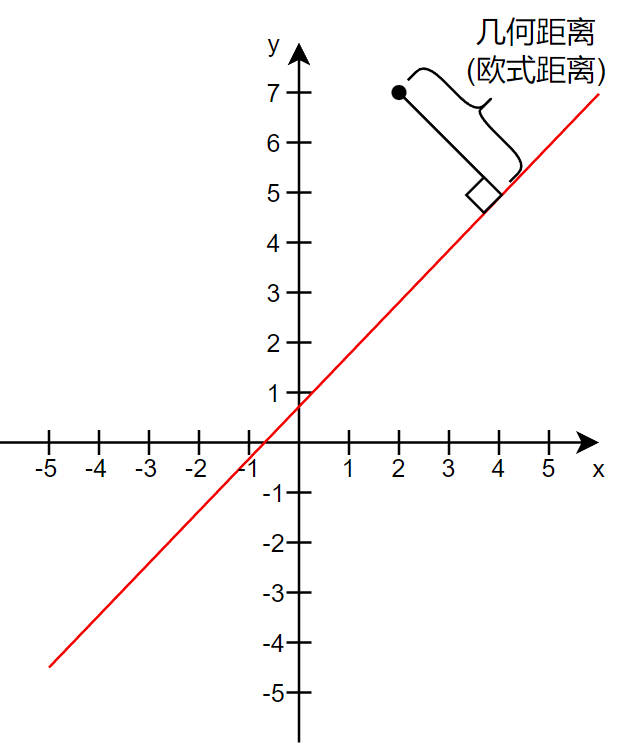
几何距离又叫欧式距离，是指一个点到直线的最短距离（垂线长度）：

$$\begin{array}{r}{d}_i=\frac{|k{x}_i+b-y_i|}{\sqrt{1+k^2}}\end{array}$$

所有点到直线几何距离之和则为：

$$\begin{array}{r}L(k,b)=\sum _{i=1}^n{d}_i=\sum _{i=1}^n\frac{|k{x}_i+b-y_i|}{\sqrt{1+k^2}}\end{array}$$

由于绝对值计算在一些求导场景计算比较繁琐，同时考虑到绝对值函数的值域为[0, +∞)，且二次平方函数在[0, +∞)内单调递增，因此通常用平方和代替绝对值和。于是几何距离拟合解也就是求点到直线损失函数最小时k和b的值：

$$\begin{array}{r}\underset{k,b}{\min }L(k,b)=\underset{k,b}{\min }\sum _{i=1}^n{d}_i^2=\underset{k,b}{\min }\sum _{i=1}^n\frac{(k{x}_i+b-y_i{)}^2}{1+k^2}\end{array}$$

2.2 残差

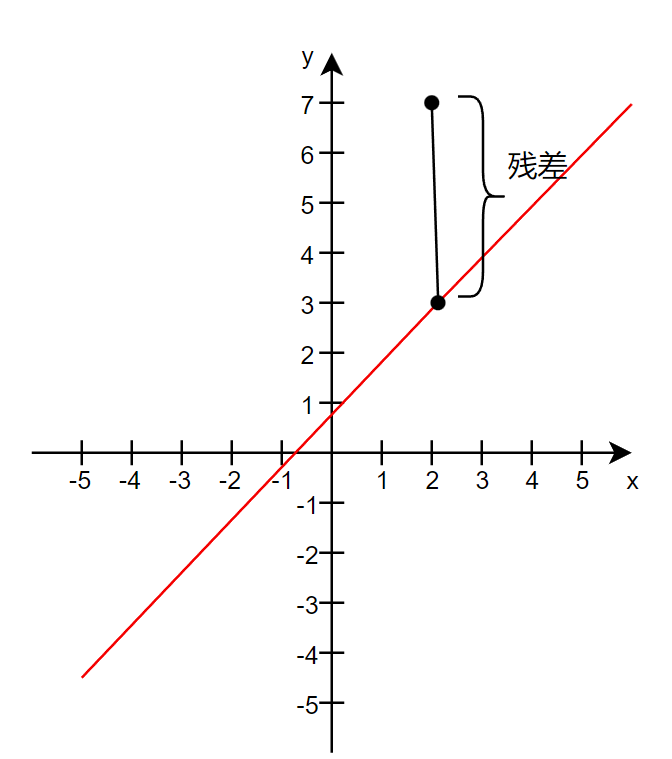
残差是指垂直方向上的偏差，对应数学表达式为：

$$\begin{array}{r}{d}_i=|k{x}_i+b-y_i|\end{array}$$

所有点到直线残差距离之和则为：

$$\begin{array}{r}L(k,b)=\sum _{i=1}^n{d}_i=\sum _{i=1}^n|k{x}_i+b-y_i|\end{array}$$

用平方和（也叫误差平方和，Sum of Squared Error，SSE）代替绝对值求拟合解也就是求点到直线残差平方和最小时k和b的值：

$$\begin{array}{r}\underset{k,b}{\min }L(k,b)=\underset{k,b}{\min }\sum _{i=1}^n{d}_i^2=\underset{k,b}{\min }\sum _{i=1}^n(k{x}_i+b-y_i{)}^2\end{array}$$

也常用均方差（Mean Squared Error, MSE），即误差平方和的平均值：
$$\begin{array}{r}\underset{k,b}{\min }L(k,b)=\underset{k,b}{\min }\sum _{i=1}^n\frac{d_i^2}{n}=\underset{k,b}{\min }\sum _{i=1}^n\frac{(k{x}_i+b-y_i{)}^2}{n}=\underset{k,b}{\min }\frac{1}{n}\sum _{i=1}^n(k{x}_i+b-y_i{)}^2\end{array}$$

2.3 为什么线性回归使用残差而非几何距离？

【知识点补充】

微分商法则：

$$z=\frac{f(x)}{g(x)}，则\frac{\partial z}{\partial x}=\frac{f^{\prime }(x)g(x)-f(x)g^{\prime }(x)}{g^2(x)}$$

微分乘积法则：

$$z=f(x)g(x)，则\frac{\partial z}{\partial x}=f^{\prime }(x)g(x)+f(x)g^{\prime }(x)$$

微分链式法则：

$$z=f(g(x))，则\frac{\partial z}{\partial x}=f^{\prime }(g(x))g^{\prime }(x)$$

• 问题背景：在回归问题中，我们假设自变量x没有误差（或误差很小可以忽略不记），而因变量y存在误差，因此，我们只考虑y方向上的偏差。
• 计算简便：最小化垂直距离的平方和可以得到一个关于k和b的闭式解（通过求导即可得到正规方程）。而最小化几何距离的平方会导致问题变得复杂（例如损失函数对k求偏导，分母含有k的二次项，求导后是非线性方程，没有解析解，需要迭代方法）。

$$\begin{array}{r}\frac{\partial d_i^2}{\partial k}=\frac{\partial }{\partial k}\left[\frac{(kx+b-y{)}^2}{1+k^2}\right]=\frac{2(kx+b-y)(x(1+k^2)-k(kx+b-y))}{(1+k^2{)}^2}\end{array}$$

$$\begin{array}{r}\frac{\partial d_i^2}{\partial b}=\frac{\partial }{\partial b}\left[\frac{(kx+b-y{)}^2}{1+k^2}\right]=\frac{2(kx+b-y)}{1+k^2}\end{array}$$

残差偏导则会简单很多：

$$\begin{array}{r}\frac{\partial d_i^2}{\partial k}=\frac{\partial (kx+b-y{)}^2}{\partial k}=2(kx+b-y)x\end{array}$$

$$\begin{array}{r}\frac{\partial d_i^2}{\partial b}=\frac{\partial (kx+b-y{)}^2}{\partial b}=2(kx+b-y)\end{array}$$

• 可解释性：垂直距离对应于我们想要预测的y值的误差，而几何距离则没有直接的预测解释。

三、矩阵计算

【下面这段是上图的latex语法代码，CSDN好像这块支持的不太好显示不出来，但我还是保留下来了，如果有用到这些语法的可以参考下】

【知识点补充】

矩阵的乘法：

$$
\begin{bmatrix}
a_{11} & a_{12} & \dots & a_{1n} \
a_{21} & a_{22} & \dots & a_{2n} \
\vdots & \vdots & \ddots & \vdots \
a_{m1} & a_{m2} & \dots & a_{mn} \
\end{bmatrix}
\begin{bmatrix}
b_{11} & b_{12} & \dots & b_{1m} \
b_{21} & b_{22} & \dots & b_{2m} \
\vdots & \vdots & \ddots & \vdots \
b_{n1} & b_{n2} & \dots & b_{nm} \
\end{bmatrix}

\begin{bmatrix}
c_{11} & c_{12} & \dots & c_{1m} \
c_{21} & c_{22} & \dots & c_{2m} \
\vdots & \vdots & \ddots & \vdots \
c_{m1} & c_{m2} & \dots & c_{mn} \
\end{bmatrix}
$$

其中：

$$c_{ij}=a_{i1}{b}_{1j}+a_{i2}{b}_{2j}+\cdots +a_{ij}{b}_{ji}$$

例如

$$
\begin{bmatrix}
1 & 2 & 3 \
4 & 5 & 6 \
7 & 8 & 9
\end{bmatrix}
\begin{bmatrix}
2 \
4 \
6
\end{bmatrix}

\begin{bmatrix}
1 \times 2 + 2 \times 4 + 3 \times 6 \
4 \times 2 + 5 \times 4 + 6 \times 6 \
7 \times 2 + 8 \times 4 + 9 \times 6
\end{bmatrix}

\begin{bmatrix}
28 \
64 \
100
\end{bmatrix}
$$

假设n个点的坐标如下：

$$(x_1,y_1),(x_2,y_2),...(x_n,y_n)$$

把x和y轴坐标分别写成矩阵形式，则有：

$$X=\left[\begin{array}{cccc}{x}_1& x_2& \dots & x_n\end{array}\right]$$

$$Y=\left[\begin{array}{c}{y}_1\\ y_2\\ \dots \\ y_n\end{array}\right]$$

把前面章节提到的拟合直线的斜率k和截距b定义成矩阵W：

$$W=\left[\begin{array}{c}k\\ b\end{array}\right]$$

并把kx + b计算出来的实际值y定义成矩阵 Y’ （注意 Y 与 Y’ 两个矩阵的差别）：

$$Y^{\prime }=\left[\begin{array}{c}k{x}_1+b\\ k{x}_2+b\\ \dots \\ k{x}_n+b\end{array}\right]$$

仔细观察可以发现，如果把矩阵 X 转置后加上一列全为1的数组成一个新的矩阵，再把该矩阵与W矩阵相乘，就得到了 Y’ 矩阵：

【知识点补充】

矩阵的转置是将矩阵的行和列互换得到的新矩阵，用右上方加T表示。例如有矩阵A：

$$A=\left[\begin{array}{ccc}1& 2& 3\end{array}\right]$$

则A的转置矩阵为

$$A^T=\left[\begin{array}{c}1\\ 2\\ 3\end{array}\right]$$

$$\begin{array}{r}{X}^{\prime }=X^T加上全为1的列=\left[\begin{array}{cc}{x}_1& 1\\ x_2& 1\\ \dots & 1\\ x_n& 1\end{array}\right]\end{array}$$

乘以W矩阵：

$$\begin{array}{r}{Y}^{\prime }=X^{\prime }\cdot W=\left[\begin{array}{cc}{x}_1& 1\\ x_2& 1\\ \dots & 1\\ x_n& 1\end{array}\right]\left[\begin{array}{c}k\\ b\end{array}\right]=\left[\begin{array}{c}k{x}_1+b\\ k{x}_2+b\\ \dots \\ k{x}_n+b\end{array}\right]\end{array}$$

我们以前文的均方误差作为损失函数，则损失函数为：

$$\begin{array}{r}L(k,b)=L(W)=\frac{1}{n}\sum _{i=1}^n(k{x}_i+b-y_i{)}^2=\frac{1}{n}|X^{\prime }W-Y{|}^2=\frac{1}{n}|Y^{\prime }-Y{|}^2\end{array}$$

三、正规方程求解与梯度下降求解

现在我们要求上述方程 W (也就是k和b)的值，使得整个损失函数最小，通常可以使用正规方程求解或者梯度下降求解。

3.1 正规方程求解

$$L(k,b)=L(W)=\frac{1}{n}|X^{\prime }W-Y{|}^2=\frac{1}{n}(W^T{X}^{\prime T}{X}^{\prime }W-2X^{\prime T}{W}^{T}Y+Y^{T}Y)$$

损失函数是向量 W 的二次函数，求极小值需令梯度为零：

$${\nabla }_{W}L(W)=0$$

计算梯度：

$${\nabla }_{W}L(W)=\frac{1}{n}(2X^{\prime T}{X}^{\prime }W-2X^{\prime T}Y)=\frac{2}{n}(X^{\prime T}{X}^{\prime }W-X^{\prime T}Y)$$

令梯度为0，也就是：

$${\nabla }_{W}L(W)=\frac{2}{n}(X^{\prime T}{X}^{\prime }W-X^{\prime T}Y)=0$$

也就是：

$$X^{\prime T}{X}^{\prime }W=X^{\prime T}Y$$
$$W=(X^{\prime T}{X}^{\prime }{)}^{-1}(X^{\prime T}Y)$$

虽然正规方程存在解析解，但这种计算方法在实际应用中有重大缺陷：

问题类型	原因	后果
计算复杂度高	矩阵求逆 $O(n^3)$ 复杂度	特征维度 > 10,000 时计算不可行
内存消耗大	需要存储 $X^{T}X$ (n×n 矩阵)	当 n > 100,000 时容易内存溢出
数值不稳定性	$X^{T}X$可能不可逆（共线性）	求解失败或结果错误
在线学习限制	需要全部数据一次性计算	无法增量更新模型

3.2 梯度下降求解

梯度下降是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数，即无约束优化问题时，梯度下降（Gradient Descent）是最常采用的方法之一。梯度下降法解决了正规方程上述问题：

• 可扩展性：处理百万级样本和万级特征
• 内存高效：每次只需部分数据（小批量）
• 在线学习：支持流式数据实时更新
• 通用性：可扩展到其他模型（逻辑回归、神经网络）

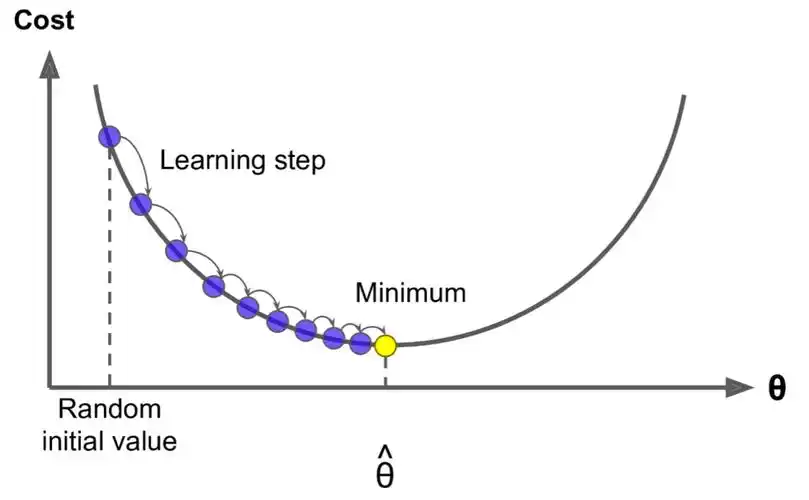
梯度下降核心思想如下（注意:=表示赋值，用于迭代计算）：

$$\begin{array}{rl}\theta & :=\theta -\alpha {\nabla }_{\theta }J(\theta )\end{array}$$

其中梯度：

$$\begin{array}{rl}{\nabla }_{\theta }J(\theta )& =\left[\begin{array}{c}\frac{\partial J}{\partial w}\\ \frac{\partial J}{\partial b}\end{array}\right]\end{array}$$

代表梯度正方向，每次从当前值$\theta$开始，减去步长$\alpha$乘以梯度${\nabla }_{\theta }J(\theta )$（也就是朝梯度的反方向前进），把计算出来的值作为新值重新赋值给$\theta$，迭代一定次数，最终趋近于所需要的结果。

四、张量（tensor）

尽管梯度下降法理论上可以求得拟合解，但如果是手动计算还是计算量过大，好在可以用计算机程序来做这些操作。我们后文用pytorch来实现梯度下降求拟合解，不过在介绍pytorch前先了解下张量这个概念。

4.1 标量(Scalar)

• 维度：0维张量。
• 定义：单个数值，没有方向，只有大小（量级）。
• 表示：通常用小写斜体字母表示，如a, b, x, 5, -3.14。
• 例子：温度(25℃)、质量(5kg)、身高(1.75m)、一个常数(π)。
• 与高维的关系：是构成向量、矩阵、张量的基本元素。可以看作是一个只有一个元素的数组。

4.2 向量(Vector)

• 维度：1维张量。
• 定义：一组有序排列的标量。通常表示在空间中既有大小又有方向的量（几何向量），或者简单地说是一列数值。
• 表示：数学/物理：通常用小写粗体字母表示，如 v, x；计算机科学/编程：常表示为一维数组，如 [1, 2, 3]。
• 结构：包含n个元素的行向量可以表示为：

$$\left[\begin{array}{cccc}{v}_1& v_2& \dots & v_n\end{array}\right]$$

包含n个元素的列向量可以表示为：

$$\left[\begin{array}{c}{v}_1\\ v_2\\ \dots \\ v_n\end{array}\right]$$

• 例子：空间中的位置坐标[x, y, z]、速度向量[vx, vy]、一个数据样本的特征向量[年龄, 收入, 信用分]。
• 与高维的关系：是矩阵的一行或一列，是张量的一个轴。由多个标量组成。

4.3 矩阵(Matrix)

• 维度：2维 张量。
• 定义：一个矩形网格（二维数组），由标量元素按行和列排列组成。
• 表示：数学：通常用大写粗体字母表示，如A, M；计算机科学/编程：表示为二维数组，如 [[1, 2, 3], [4, 5, 6]]。
• 结构： 有m行和n列的矩阵：

$$\left[\begin{array}{cccc}{a}_{11}& a_{12}& \dots & a_{1n}\\ a_{21}& a_{22}& \dots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m1}& a_{m2}& \dots & a_{mn}\end{array}\right]$$

• 例子：灰度图像（每个像素一个灰度值）、线性方程组中的系数矩阵、数据集（行代表样本，列代表特征）、图的邻接矩阵。
• 与高维的关系：是张量的一个特例（当阶数=2时）。由多个向量（行向量或列向量）组成。其元素是标量。

4.4 张量(Tensor)

• 维度：N维张量(N >= 0)。标量、向量、矩阵都是张量的特例。
• 定义：多维数组概念的一般化。张量由其阶数（阶数或秩） 定义，阶数就是它拥有的轴数（维度数）。每个轴对应一个维度长度（大小）。
• 表示：数学/物理：通常用特殊字体或大写字母表示，如T；计算机科学/编程（深度学习框架）：表示为N维数组，是核心数据结构。在NumPy中是ndarray，在TensorFlow/PyTorch中是Tensor。
• 结构：阶数/秩：轴（维度）的数量；形状：一个元组，表示每个轴的长度。
• 例子：0阶张量：标量 (42)；1阶张量：向量 ([1, 2, 3])；2阶张量：矩阵 ([[1, 2], [3, 4]])；3阶张量：RGB 图像 (高度 x 宽度 x 3个颜色通道)；4阶张量：一批 RGB 图像 (批量大小 x 高度 x 宽度 x 通道数)；物理中的张量：应力张量 (2阶，3x3)、电磁场张量 (2阶，4x4，相对论中)。
• 与低维的关系：标量是0阶张量；向量是1阶张量；矩阵是2阶张量；N阶张量 (N>2) 是更高维度的数据容器，无法用简单的行列表格表示。

五、pytorch线性回归求拟合解

5.1 自动微分（Autograd）

可以把复杂的计算抽象成一张图（graph），如下图所示。

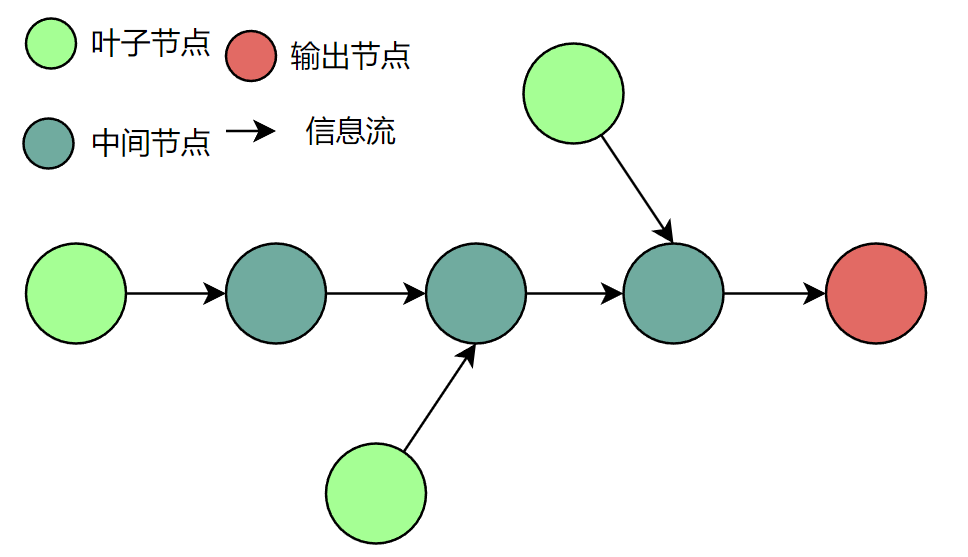
在一张图中可以划分为三种节点，这三种节点在pytorch中对应的都是Tensor：

• 叶子节点：图的末端，没有信息流经过，通常对应输入值
• 中间节点：有信息流经过且不是末端的节点
• 输出节点：图的末端，信息流在这里结束

前文提到的计算矩阵与梯度下降求（偏）导在pytorch中有个重要概念，叫Autograd（自动微分），是pytorch神经网络优化的核心。Tensor在自动微分上有三个重要属性：

• requires_grad：布尔值，默认False，为True时表示该Tensor需要自动微分。
• grad：用于存储微分值
• grad_fn：用于存储微分函数

当叶子节点的requires_grad为True时，信息流经过该节点时，所有中间节点的requires_grad属性都会变成True，只要在输出节点调用反向传播函数backward()，就会自动求出叶子节点的微分值并更新存储到叶子节点的grad属性中。注意：只有叶子节点的grad属性能被更新。

所以反向传播指的就是求微分的过程，而与之对应的概念叫前向传播，前向传播指的是从叶子节点开始追踪信息流并记录下整个过程使用的函数，直到输出节点。

5.2 代码实现

5.2.1 准备数据

我们先用一段程序准备 X 和 Y的值，其中$y‌\approx 1.2x+3$，也就是前面章节提到的k = 1.2，b = 3，$W=\left[\begin{array}{c}1.2\\ 3\end{array}\right]$：

# init_data.py
import torchx = torch.linspace(-5, 5, 50)
y = 1.2 * x + 3 + 0.2 * torch.rand(x.size())// x、y默认是50行一列的矩阵，t()方法是转置，即把结果变成1行50列的矩阵
print(x)
print(y)

为了固定初始数据，我们取一次输出结果：

$ python init_data.py
tensor([[-5.0000, -4.7959, -4.5918, -4.3878, -4.1837, -3.9796, -3.7755, -3.5714,-3.3673, -3.1633, -2.9592, -2.7551, -2.5510, -2.3469, -2.1429, -1.9388,-1.7347, -1.5306, -1.3265, -1.1224, -0.9184, -0.7143, -0.5102, -0.3061,-0.1020,  0.1020,  0.3061,  0.5102,  0.7143,  0.9184,  1.1224,  1.3265,1.5306,  1.7347,  1.9388,  2.1429,  2.3469,  2.5510,  2.7551,  2.9592,3.1633,  3.3673,  3.5714,  3.7755,  3.9796,  4.1837,  4.3878,  4.5918,4.7959,  5.0000]])
tensor([[-2.9354, -2.6106, -2.5070, -2.1573, -2.0062, -1.7503, -1.3872, -1.2434,-1.0399, -0.7758, -0.3666, -0.2873, -0.0095,  0.3227,  0.4873,  0.8658,1.0763,  1.2531,  1.4564,  1.7801,  2.0736,  2.1845,  2.4290,  2.6380,2.9424,  3.3018,  3.3983,  3.6191,  4.0433,  4.1419,  4.5190,  4.7428,4.9229,  5.1000,  5.4449,  5.7140,  5.8567,  6.1416,  6.3126,  6.6015,6.9624,  7.1786,  7.4084,  7.5916,  7.9413,  8.1177,  8.4207,  8.5427,8.8767,  9.1533]])

5.2.2 训练

首先我们基于上述数据准备好输入数据x与目标数据y：

x = torch.Tensor([-5.0000, -4.7959, -4.5918, -4.3878, -4.1837, -3.9796, -3.7755, -3.5714, -3.3673, -3.1633, -2.9592, -2.7551,-2.5510, -2.3469, -2.1429, -1.9388, -1.7347, -1.5306, -1.3265, -1.1224, -0.9184, -0.7143, -0.5102, -0.3061,-0.1020, 0.1020, 0.3061, 0.5102, 0.7143, 0.9184, 1.1224, 1.3265, 1.5306, 1.7347, 1.9388, 2.1429, 2.3469, 2.5510,2.7551, 2.9592, 3.1633, 3.3673, 3.5714, 3.7755, 3.9796, 4.1837, 4.3878, 4.5918, 4.7959, 5.0000])
y = torch.Tensor([-2.9354, -2.6106, -2.5070, -2.1573, -2.0062, -1.7503, -1.3872, -1.2434, -1.0399, -0.7758, -0.3666, -0.2873,-0.0095, 0.3227, 0.4873, 0.8658, 1.0763, 1.2531, 1.4564, 1.7801, 2.0736, 2.1845, 2.4290, 2.6380, 2.9424, 3.3018,3.3983, 3.6191, 4.0433, 4.1419, 4.5190, 4.7428, 4.9229, 5.1000, 5.4449, 5.7140, 5.8567, 6.1416, 6.3126, 6.6015,6.9624, 7.1786, 7.4084, 7.5916, 7.9413, 8.1177, 8.4207, 8.5427, 8.8767, 9.1533])

在(15)式中，我们提到要对x做个转置并且增加一列全为1的列。其中one()函数是创建元素全为1的Tensor，stack()函数则是沿某维度对Tensor序列进行连接，torch.stack((x, x0), dim=1)就是把x和x0按列方向进行连接，也就是把x转置后增加一列全为1的列：

x0 = torch.ones(x.numpy().size)
inputs = torch.stack((x, x0), dim=1)

W（前文k和b组成的向量）初始时使用随机数：

w = torch.randn(2, requires_grad=True)

接下来我们要定义训练函数，函数输入分别为输入inputs、目标值target、k/b（权重）矩阵w、训练次数times（默认50）和步长step（默认0.01）：

def train(inputs, target, w, times=50, step=0.01):global loss, outputfor i in range(times):output = inputs.mv(w)loss = (output - target).pow(2).sum()loss.backward()w.data -= step * w.gradw.grad.zero_()print(w)print(loss)draw_result(output, loss)return w, loss

for循环训练完后打印训练后得到的权重矩阵和损失值，并使用draw_result()函数用可视化图表形式展示原始数据点和最终权重拟合方程的关系。并使用draw_result函数如下：

def draw_result(output, loss):plt.scatter(x.numpy(), y.numpy())plt.plot(x.numpy(), output.data.numpy(), 'r-', lw=2)plt.text(0.5, 0, 'loss=%s' % loss.item())plt.show()

最后再让上述逻辑串起来：

x0 = torch.ones(x.numpy().size)
inputs = torch.stack((x, x0), dim=1)
outputs = y
w = torch.randn(2, requires_grad=True)
# 训练100000次，步长为1e-4
w, loss = train(inputs, outputs, w, times=100000, step=1e-4)

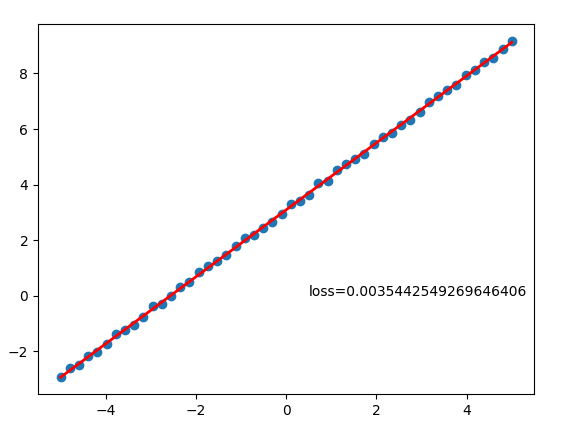
最终得到如下结果，也就是计算出k = 1.2042，b = 3.0891，损失值为0.0035，与初始化数据时的：

$ python liner.py
tensor([1.2042, 3.0891], requires_grad=True)
tensor(0.0035, grad_fn=<MeanBackward0>)

结果图：

完整代码：

# liner.py
import torch
import matplotlib.pyplot as pltx = torch.Tensor([-5.0000, -4.7959, -4.5918, -4.3878, -4.1837, -3.9796, -3.7755, -3.5714, -3.3673, -3.1633, -2.9592, -2.7551,-2.5510, -2.3469, -2.1429, -1.9388, -1.7347, -1.5306, -1.3265, -1.1224, -0.9184, -0.7143, -0.5102, -0.3061,-0.1020, 0.1020, 0.3061, 0.5102, 0.7143, 0.9184, 1.1224, 1.3265, 1.5306, 1.7347, 1.9388, 2.1429, 2.3469, 2.5510,2.7551, 2.9592, 3.1633, 3.3673, 3.5714, 3.7755, 3.9796, 4.1837, 4.3878, 4.5918, 4.7959, 5.0000])
y = torch.Tensor([-2.9354, -2.6106, -2.5070, -2.1573, -2.0062, -1.7503, -1.3872, -1.2434, -1.0399, -0.7758, -0.3666, -0.2873,-0.0095, 0.3227, 0.4873, 0.8658, 1.0763, 1.2531, 1.4564, 1.7801, 2.0736, 2.1845, 2.4290, 2.6380, 2.9424, 3.3018,3.3983, 3.6191, 4.0433, 4.1419, 4.5190, 4.7428, 4.9229, 5.1000, 5.4449, 5.7140, 5.8567, 6.1416, 6.3126, 6.6015,6.9624, 7.1786, 7.4084, 7.5916, 7.9413, 8.1177, 8.4207, 8.5427, 8.8767, 9.1533])def draw_result(output, loss):plt.scatter(x.numpy(), y.numpy())plt.plot(x.numpy(), output.data.numpy(), 'r-', lw=2)plt.text(0.5, 0, 'loss=%s' % loss.item())plt.show()def train(inputs, target, w, times=50, step=0.01):global loss, outputfor i in range(times):output = inputs.mv(w)loss = (output - target).pow(2).sum()loss.backward()w.data -= step * w.gradw.grad.zero_()print(w)print(loss)draw_result(output, loss)return w, lossx0 = torch.ones(x.numpy().size)
inputs = torch.stack((x, x0), dim=1)
outputs = y
w = torch.randn(2, requires_grad=True)
w, loss = train(inputs, outputs, w, times=100000, step=1e-4)

5.3 cuda GPU加速

为了计算训练时长，我们引入time包的perf_counter计时，把输训练数据加大到50w，并去掉绘图相关步骤：

import torch
from time import perf_counterx = torch.linspace(-5, 5, 500000)
y = 1.2 * x + 3 + 0.2 * torch.rand(x.size())def train(inputs, target, w, times=50, step=0.01):global loss, outputfor i in range(times):output = inputs.mv(w)loss = (output - target).pow(2).sum()loss.backward()w.data -= step * w.gradw.grad.zero_()print(w)print(loss)return w, lossx0 = torch.ones(x.numpy().size)
inputs = torch.stack((x, x0), dim=1)
outputs = y
w = torch.randn(2, requires_grad=True)start = perf_counter()
w, loss = train(inputs, outputs, w, times=100000, step=1e-4)
end = perf_counter()
time = end - start
print("time: %s" % time)

再次执行查看训练耗时，结果为39s左右，这是纯cpu的计算结果：

$ python liner.py
$ python liner.py
tensor([nan, nan], requires_grad=True)
tensor(nan, grad_fn=<SumBackward0>)
time: 290.2266564950005

下面我们引入cuda GPU计算：

import torch
import matplotlib.pyplot as plt
from time import perf_counterx = torch.linspace(-5, 5, 500000)
y = 1.2 * x + 3 + 0.2 * torch.rand(x.size())def train(inputs, target, w, times=50, step=0.01):global loss, outputfor i in range(times):output = inputs.mv(w)loss = (output - target).pow(2).sum()loss.backward()w.data -= step * w.gradw.grad.zero_()print(w)print(loss)# draw_result(output, loss)return w, lossx0 = torch.ones(x.numpy().size)
inputs = torch.stack((x, x0), dim=1)
outputs = y
w = torch.randn(2)if torch.cuda.is_available():inputs = inputs.cuda()outputs = outputs.cuda()w = w.cuda()w.requires_grad = Trueprint("cuda available")
else:inputs = inputsoutputs = outputsw = ww.requires_grad = Truestart = perf_counter()
w, loss = train(inputs, outputs, w, times=100000, step=1e-4)
end = perf_counter()
time = end - start
print("time: %s" % time)

查看运行结果，不到45s，相比cpu的290s，有了很大的提升：

$ python liner.py
cuda available
tensor([nan, nan], device='cuda:0', requires_grad=True)
tensor(nan, device='cuda:0', grad_fn=<SumBackward0>)
time: 44.49189568300062

六、梯度下降法求拟合解存在的问题

从上述结果来看，我们用梯度下降法+pytorch了解了线性回归的计算过程，但在实际案例中，梯度下降法可能存在以下问题需要注意。

6.1 局部极小值（Local Minima）

• 问题：在非凸函数（如神经网络）中，损失函数可能存在多个“山谷”。梯度下降可能收敛到某个局部最低点（局部极小值），而非全局最低点（全局最小值）。
• 后果：模型性能次优。
• 缓解方法
  • 使用随机梯度下降（SGD）引入噪声跳出局部极小值。
  • 模拟退火、动量优化（Momentum）等技术。

6.2 鞍点问题（Saddle Points）

• 问题：在高维空间中，梯度接近零的点可能是鞍点（一个方向上升，另一方向下降），而非局部极小值。梯度下降会在此停滞。
• 后果：优化速度大幅下降，尤其影响深度学习。
• 数学形式：Hessian矩阵有正负特征值。
• 缓解方法：
  • 自适应学习率算法（如 Adam、RMSProp）。
  • 二阶优化（如牛顿法，但计算代价高）。

6.3 学习率选择困难

• 问题：
  • 学习率过大：损失函数震荡甚至发散（跳过最优解）。
  • 学习率过小：收敛极慢，易陷入局部极小值。
• 缓解方法：
  • 学习率调度（如指数衰减、余弦退火）。
  • 自适应算法（AdaGrad, Adam 等动态调整学习率）。

6.4 梯度消失/爆炸（Vanishing/Exploding Gradients）

• 问题：
  • 梯度消失：深层网络中，梯度连乘后趋近于零（如Sigmoid激活函数），导致底层参数无法更新。
  • 梯度爆炸：梯度连乘后极大（如RNN），导致参数更新溢出。
• 后果：模型无法训练或数值不稳定。
• 缓解方法：
  • 梯度裁剪（Gradient Clipping）。
  • 使用 ReLU 及其变体替代Sigmoid/Tanh。
  • 残差连接（ResNet）、批量归一化（BatchNorm）。

6.5 批量选择的影响

• 问题：
  • 批量梯度下降（BGD）：计算全数据集梯度，内存需求大、速度慢。
  • 随机梯度下降（SGD）：单样本更新，噪声大、震荡强。
  • 小批量梯度下降（Mini-batch GD）：需手动调批量大小（Batch Size）。
    • 批量过小 → 噪声大、收敛不稳定。
    • 批量过大 → 内存不足、陷入尖锐极小值（泛化性差）。
• 缓解方法：根据硬件和数据集调整批量大小（常用32-256）。

6.6 特征尺度差异（Feature Scaling）

• 问题：若特征量纲差异大（如年龄∈[0,100] vs 收入∈[0,1000000]），损失函数的等高线呈“狭长山谷”状。
• 后果：梯度下降路径震荡，收敛缓慢。
• 解决方法：标准化（Standardization）或归一化（Normalization）。

6.7 收敛判断与停止条件

• 问题：
  • 何时停止迭代？损失函数可能长期波动但未收敛。
  • 提前停止（Early Stopping）需验证集，可能浪费计算资源。
• 缓解方法：
  • 设置最大迭代次数。
  • 监控验证集损失/精度。
  • 设定阈值（如连续10次损失下降<$1e^{-5}$）。

6.8 计算效率与内存限制

• 问题：
  • 大规模数据集下，BGD需遍历全数据计算梯度，计算开销大。
  • 高维参数（如深度学习）需存储海量梯度，内存压力大。
• 缓解方法：
  • 小批量梯度下降（Mini-batch GD）。
  • 分布式计算（如Parameter Server）。
  • 梯度压缩技术。

6.9 非光滑函数的不可导点

• 问题：使用ReLU等激活函数时，函数在零点不可导。
• 后果：梯度计算失效。
• 解决方法：使用次梯度（Subgradient）或近似梯度（如ReLU在0点取0或1）。