【*正确*题解|两种做法】 [JLOI2013] 洛谷 P3256 赛车[半平面交/单调栈]

很折磨的一道题，，调了特别久特别恶心。

前置知识：

半平面交相关知识

可以看我超多图的半平面交笔记

题面：

洛谷P3256

（我第一次看题的时候把起跑线前想成了起跑线后，还纳闷这样例为啥不对。。

关于样例输出为什么有 1，因为一开始它与起跑线的距离是全场最大的之一，也可以得奖）

解析：

（1）半平面交做法

既然是半平面交，就考虑构造很多相交的直线。

我们可以把起跑线前的距离当 y 轴，时间当 x 轴，那么样例的赛车们就可以这样表述：

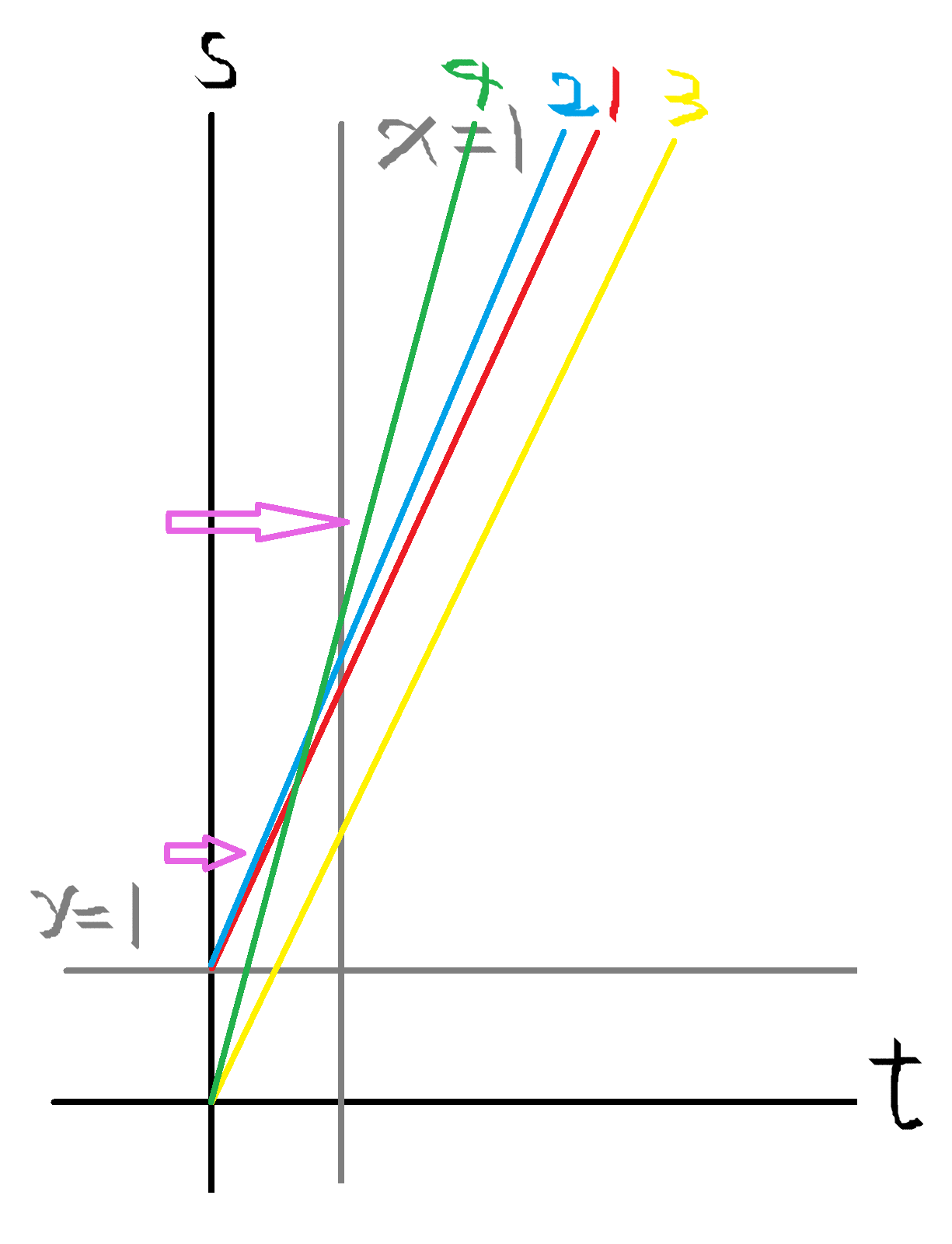
（这个图为了形式画的很不标准！！只是用来演示题面与半平面交的关系）

这样就很明了，最里面的直线围成的多边形，它的轮廓上的线段们就是答案。

（因为在同一 x 的情况下，最靠上的能得奖，总体的围成的图像也就在左上）

直接半平面交，用 x = 0 和 x = 1 连线建图，最后输出双端队列里的所有线。

然而，这题有个线与线之间的斜率差很小的数据，甚至到了需要把精度精确到 1e-18 的程度！

所以把 eps = 1e-18，不要忘记开 long double。

还有个小问题，虽然数据中没有两条完全一样的线，但按照题面是有这种情况的。

比如说这组 hack 数据：

5 
0 2 2 4 4 
4 3 3 2 0

输出：

5

1 2 3 4 5

而半平面交处理会跳过两条一样的线，所以一开始的时候要把一样的线放进同一个 vector 里。

之后输出时，看看这个线有没有 vector 线，有的话一起输出。

代码：

还有些细节，我写注释里了。

#include<bits/stdc++.h>
using namespace std;
#define double long double   //long double const int N = 1e4 + 10;
const double eps = 1e-18;  //对double无效，对long double有效struct point {double x, y;
} ;
struct line {point s, e;int id;
} a[N], q[N];point operator+(point a, point b) {return {a.x + b.x, a.y + b.y};
}point operator-(point a, point b) {return {a.x - b.x, a.y - b.y};
}point operator*(point a, double t) {return {a.x * t, a.y * t};
}double operator*(point a, point b) {return a.x * b.y - a.y * b.x;
}double angle(line a) {return atan2(a.e.y - a.s.y, a.e.x - a.s.x);
}bool cmp(line a, line b) {double A = angle(a), B = angle(b);if (fabs(A - B) > eps) {return A < B;}else {return (a.e - a.s) * (b.e - a.s) < 0;}
}point cross(line a, line b) {point u = a.s - b.s;point v = a.e - a.s;point w = b.e - b.s;double t = (u * w) / (w * v);return a.s + v * t;
}bool right(line a, line b, line c) {point p = cross(b, c);return (a.e - a.s) * (p - a.s) < 0;  //这里可不能等于 0！//当后面那个向量为 (0, 0) 的时候，我们也不应该把队尾踢出去 
}int n, m, ans[N], len;
int vel[N], pos[N];
map<int, map<int, int>> mp;   //辅助 vector存相同线的 map，必须这样开不然会炸 
vector<int> G[N];void half_plane(){n++;a[n] = { {0, 1}, {0, 0}, 0 };   //边界线 sort( a + 1, a + n + 1, cmp );int head = 1, tail = 1;q[1] = a[1];for (int i = 2; i <= n; i++) {if ( angle(a[i]) - angle(a[i - 1]) < eps) {  //跳过相同线段 continue;}while ( head < tail && right(a[i], q[tail - 1], q[tail]) ) {tail--;}while ( head < tail && right(a[i], q[head], q[head + 1]) ) {head++;}tail++;q[tail] = a[i];}for (int i = head; i <= tail; i++) if(q[i].id != 0){len++;ans[len] = q[i].id;}int t = len;for(int i = 1; i <= t; i++) {for(auto j: G[ans[i]]) {len++;ans[len] = j;}}sort(ans + 1, ans + len + 1);cout << len << endl;for (int i = 1; i <= len; i++) {cout << ans[i] << " "; }cout << endl;
}int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> m;for (int i = 1; i <= m; i++) {cin >> pos[i];}for (int i = 1; i <= m; i++) {cin >> vel[i];}n = 0;for (int i = 1; i <= m; i++) {n++;a[n] = { {0, 1.0 * pos[i]}, {1, 1.0 * (pos[i] + vel[i])}, i };int t = mp[pos[i]][vel[i]];if (t != 0) {G[t].push_back(i);}else{mp[pos[i]][vel[i]] = i;}}half_plane();return 0;
} 

（2）单调栈做法

我不想打了，借用这位佬的题解，我做了一些改编，更加易懂：

（但是这位佬没有处理相同线，我给的代码有）

• 如果一辆车比你快（跟你一样快），还比你出发点前，你肯定追不上它。

  即如果 a.k > b.k && a.v >= b.v，则 a 追不上 b，得不到奖。

• 如果一辆车跟你一样快，还跟你出发点一样，那就会并列得奖，之前我们有说过怎么处理。

• 如果一辆车比你出发点前，但比你慢，你就有可能追上它了， 你有可能得奖。

  但可能有比你速度快的在你前面，或在后面，在你追上之前超你车。

• 如果一辆车比你快，但比你出发点后，你就有可能在拿到第一之前被超车，可能得不了奖。

综合的来说，我们先按照速度从小到大排序（线的斜率），第二关键字按距离起跑线从小到大。

（为什么从小到大？因为先处理速度快的赛车，会让后面不那么优的赛车失去得奖机会）

对于每一个即将加入单调栈的赛车：

若 a 为新加入的赛车，b 为 stk[top]，c 为 stk[top - 1]，a 追上 b 的时间小于 b 追上 c 的时间，则 b 不可能拿到第一，可以出栈。

因为在 b 追上 c 之前，a 会先追上 b，b 肯定不可能得奖。

代码：

#include<bits/stdc++.h>
using namespace std;const int N = 1e4 + 10;
int stk[N], n;
map<int, map<int, int>> mp;   //辅助 vector存相同线的 map，必须这样开不然会炸 
vector<int> G[N];struct node{double p, v;int id;
}  a[N];bool cmpa(node x, node y) {return x.p < y.p;
}bool cmpb(node x, node y){if (x.v == y.v) return x.p < y.p;return x.v < y.v;
}bool cmpc(int x, int y){return x < y;
}double calc(node a, node b){   //计算追及时间if (a.v == b.v) {return 2e9;   //防止除 0，为的就是跳过两条一样的 }return double(a.p - b.p) / (b.v - a.v);
}int main() {ios::sync_with_stdio(false);cin.tie(0);cin >> n;for (int i = 1; i <= n; i++) {cin >> a[i].p;}for (int i = 1; i <= n; i++) {cin >> a[i].v;}for (int i = 1; i <= n; i++) {a[i].id = i;int t = mp[a[i].p][a[i].v];if (t != 0) {G[t].push_back(i);}else {mp[a[i].p][a[i].v] = i;}}int top = 0;sort(a + 1, a + n + 1, cmpb);top++;stk[top] = 1;for (int i = 2; i <= n; i++) {while ( (top >= 1) && ( (a[i].p > a[stk[top]].p) ||( (top>1) && calc(a[stk[top]], a[i]) < calc(a[stk[top - 1]], a[stk[top]]) ) ) ) top--;top++;stk[top] = i;}int t = top;for (int i = 1; i <= t; i++) {stk[i] = a[stk[i]].id;for(auto j: G[stk[i]]) {top++;stk[top] = j;}}sort(stk + 1, stk + top + 1, cmpc);top = unique(stk + 1, stk + top + 1) - stk - 1;cout << top << endl;for (int i = 1; i <= top; i++) {cout << stk[i] << " ";}cout << endl;return 0;
}