Leetcode 深度优先搜索 (2)

94. 二叉树的中序遍历

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

示例 1：

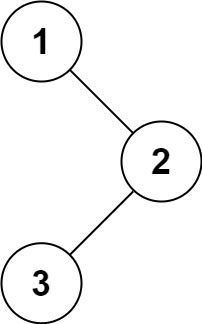
输入： root = [1,null,2,3]
输出： [1,3,2]

问题分析
中序遍历是二叉树遍历的基本方式之一，遍历顺序为：左子树 → 根节点 → 右子树

核心特点

• 递归性质：对每个节点都按照相同的规则处理
• 有序性：对于二叉搜索树，中序遍历结果是有序序列
• 深度优先：需要深入到最左侧节点才开始访问

思路一：递归方法（最直观）

基本思想：

• 利用递归的天然特性，直接按照中序遍历的定义实现
• 每次递归处理：左子树 → 当前节点 → 右子树

算法步骤：

• 如果当前节点为空，直接返回
• 归遍历左子树
• 问当前节点（添加到结果中）
• 递归遍历右子树

时间复杂度： $O(n)$ 每个节点访问一次 空间复杂度：$O(h)$ 递归栈深度，h为树高

思路二：迭代方法（使用栈）

基本思想：

• 用栈模拟递归过程
• 先将所有左子树节点入栈，然后逐个弹出处理

算法步骤：

• 从根节点开始，将所有左子树节点压入栈中
• 栈不为空时：
• 弹出栈顶节点，访问该节点
• 如果该节点有右子树，将右子树作为新的起点，重复步骤1
• 核心理解：栈中存储的是"待访问的节点"，这些节点的左子树已经处理完毕

思路三：Morris遍历（空间优化）

基本思想：

• 利用叶子节点的空指针建立临时连接
• 实现O(1)空间复杂度的遍历

算法核心：

• 对于每个节点，找到其前驱节点（左子树的最右节点）
• 建立前驱节点到当前节点的临时连接
• 遍历完成后恢复树的原始结构

代码实现

递归方法（最直观）

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();inorderHelper(root, result);return result;}/*** 中序遍历递归辅助方法* @param node 当前节点* @param result 结果列表*/private void inorderHelper(TreeNode node, List<Integer> result) {// 递归终止条件：节点为空if (node == null) {return;}inorderHelper(node.left, result);result.add(node.val);inorderHelper(node.right, result);}}

迭代方法（使用栈）

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public List<Integer> inorderTraversal(TreeNode root) {List<Integer> result = new ArrayList<>();Stack<TreeNode> stack = new Stack<>();TreeNode current = root;// 迭代过程：// 1. 先将所有左子树节点压栈// 2. 弹出节点并访问// 3. 转向右子树继续处理while (current != null || !stack.isEmpty()) {// 将当前节点及其所有左子树节点压栈while (current != null) {stack.push(current);current = current.left;}// 弹出栈顶节点（此时左子树已处理完）current = stack.pop();// 访问当前节点result.add(current.val);// 转向右子树current = current.right;}return result;}
}