原码表示法、反码表示法、移码表示法、补码表示法
数学中使用 10 进制数,并在数字前面加一个负号表示负数。计算机中采用二进制,需要找到一种表示负数的方法。
原码表示法
最朴素的方法就是原码表示法,类似于数学中数字前面是正号表示正数,是负号则表示负数。原码表示法用最高位作为符号位,符号位是 0 则表示正数,符号位是 1 则表示负数。
例如对于 8 位的原码表示法的数
0000,0101
转换为 10 进制是 +5, 正号省略不写,则表示的是 5.
要表示负数 -5,则类似于把正号改成负号那样,把
0000,0101
的最高位(最左边是最高位)改成 1,变成
1000,0101
这就是原码表示法下的 -5.
这种表示法,对于 8 位二进制位来说,实际上只有 7 位是用来表示数值大小的,因此值域是 [-127, 127] ,其中低 7 位全为 0 时表示 0, 但是此时符号位可以为 0 也可以为 1,也就是用了 2 种 2 进制组合去表示 0 这个数,有点浪费了。
原码表示法的纯小数
对于 8 位的原码表示法的数,把它看成隐含着一个分母,这个分母的值是
28−1=27=1282^{8-1} = 2^7 = 128 28−1=27=128
于是值域从原本的 [-127, 127] 变成了
[−127128,127128][-\frac{127}{128}, \frac{127}{128}] [−128127,128127]
即相当于每一位的权重发生改变了
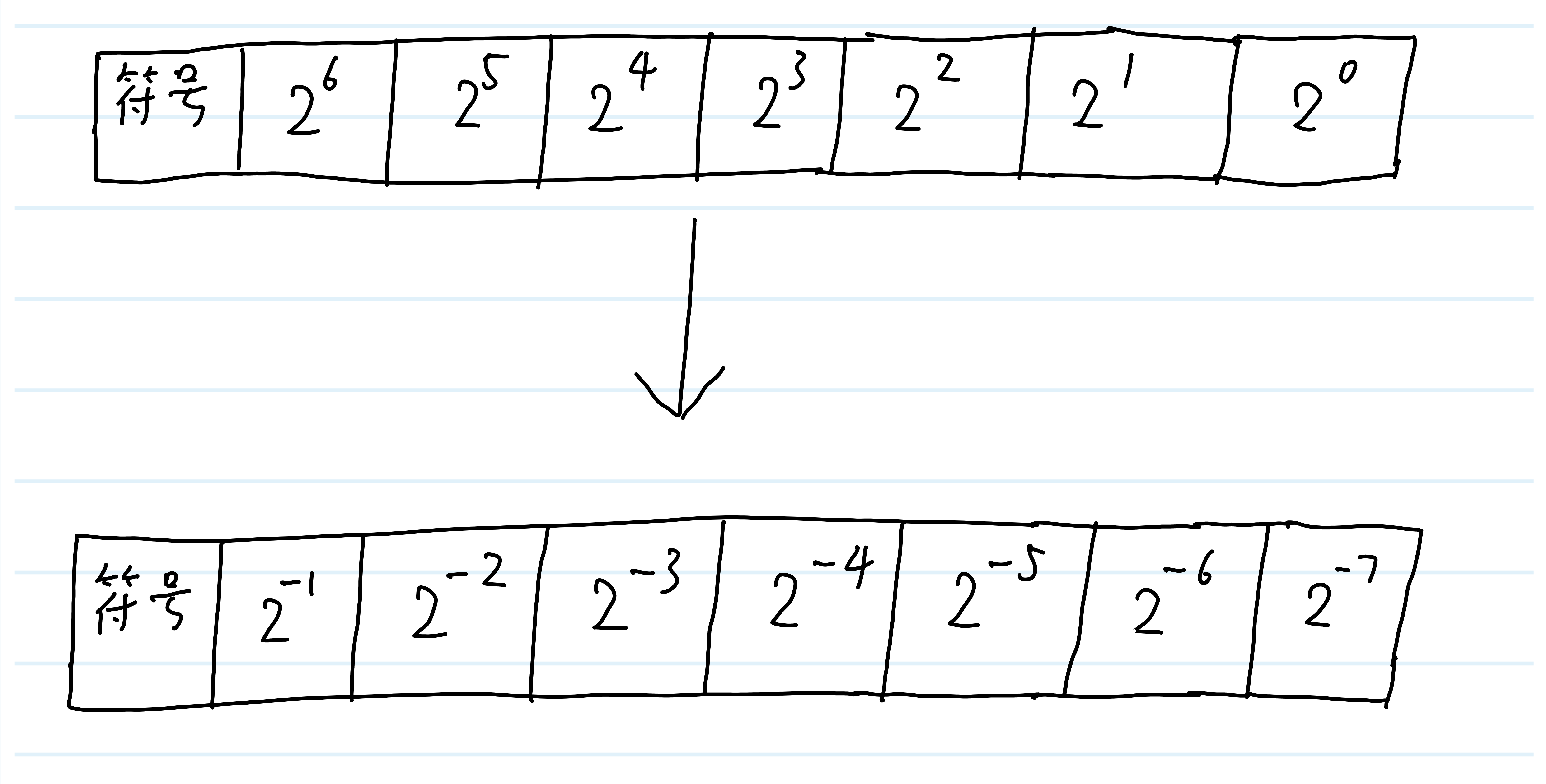
-
想要表示 +0.5,即 +12+\frac{1}2{}+21 ,就让权重是 2−12^{-1}2−1 的位为 1,其他位为 0,并且符号位为 0. 即
0100,0000. -
想要表示 -0.5,即 −12-\frac{1}2{}−21,就让权重是 2−12^{-1}2−1 的位为 1,其他位为 0,并且符号位为 1. 即
1100,0000
或者这样思考:
- 想要表示 -0.5,符号位是 1,然后因为值实际上是隐含着分母 128 的,所以要写出一个二进制原码,它的值除以 128 后等于 12\frac{1}{2}21

反码表示法
前面的原码表示法是把最高位当成正负号来用,现在的反码表示法是:
- 正数就正常写出二进制
- 如果是负数,先写出它的相反数的二进制,再进行位取反操作。
这种表示法最终的现象也是:
- 最高位为 0 时表示的是正数。
- 最高位为 1 时表示的是负数。
但是现在最高位并不再像原码表示法那样具有正负号的含义了,他只是表现出来的现象让它看起来好像是具有像正负号那样的含义。
例如表示 +5 ,把 5 转为二进制:
0000,0101
表示 -5 :
先写出它的相反数,即 5 的二进制
0000,0101
然后把每一位取反,得到
1111,1010
这就是反码表示法下的 -5
全 1 数减去 x, 相当于把 x 按位取反
以 8 位二进制数为例,列一个减法竖式
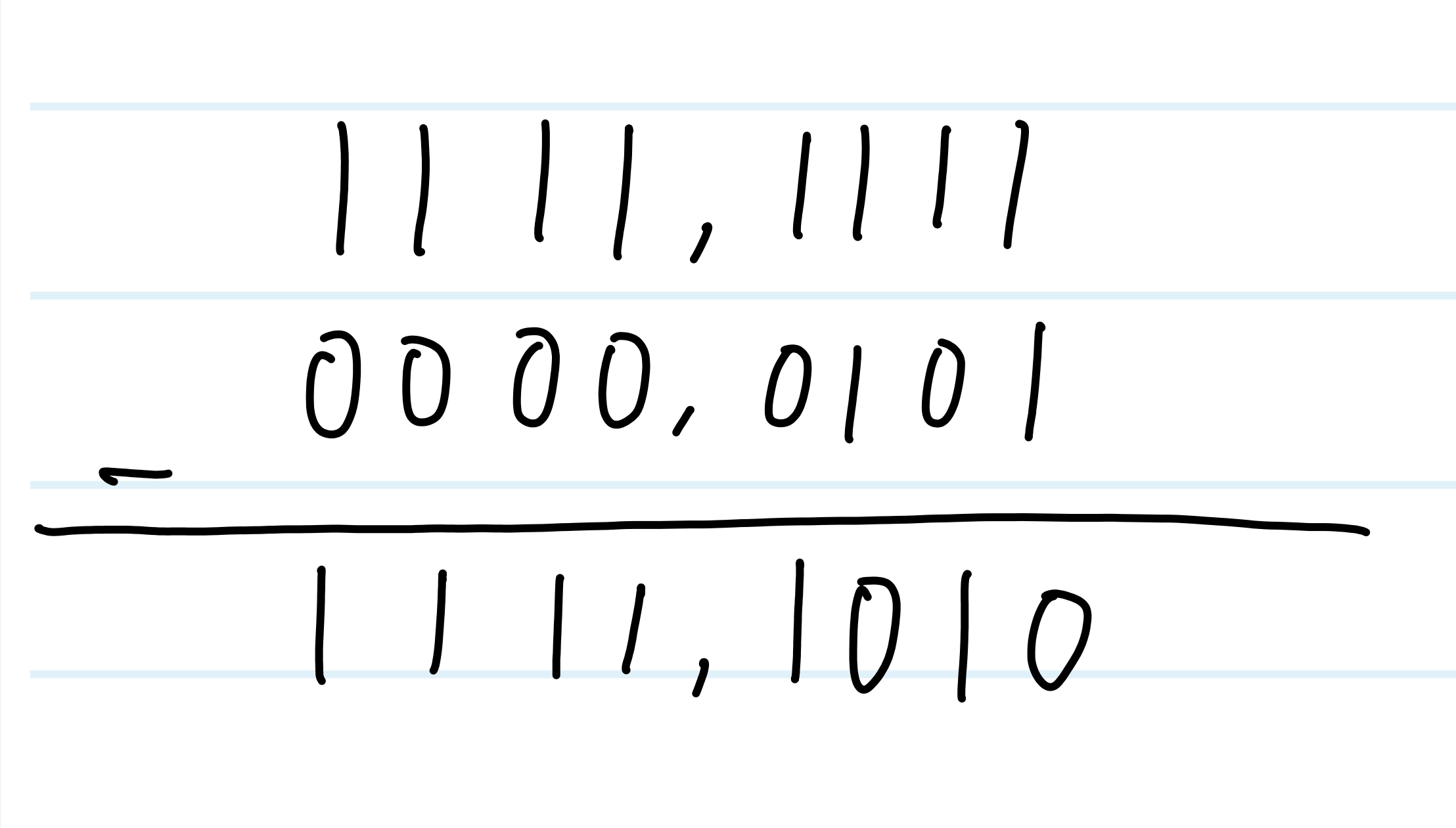
移码表示法
移码的思想也很朴素。本来二进制数只能表示正数,因为没地方给你添加一个负号来告诉计算机这是负数。除非像原码那样用最高位来模拟正负号。于是有人想出了把值域向下移动一段距离,就得到了表示负数的能力。
例如对于 8 位二进制数,本来值域是 [0, 255] ,如果向下移动 28−1=27=1282^{8-1} = 2^7 = 12828−1=27=128,则值域变成了 [-128, 127]
那怎么用移码表示 -5 呢?

移码表示法最大的问题是 0 点与无符号整型不重合,计算不方便,无法自然地进行无符号整型和有符号整型之间的转换。
下面的补码表示法就可以解决这个问题
补码表示法
补码比较复杂,见
无符号整型通过调整数轴的解释方式得到补码形式的有符号整型
