当前位置：首页 > news >正文

初学python的我开始Leetcode题15-3

news 2025/8/17 13:07:56

提示：100道LeetCode热题15-3主要是动态规划相关，包括四题：最长递增子序列、乘积最大子数组、分割等和子集、最长有效括号。由于初学，所以我的代码部分仅供参考。

前言

这是动态规划的最后几题啦，下一周我们探索多维动态规划！

提示：以下是本篇文章正文内容，下面结果代码仅供参考

题目1：最长递增子序列

1.题目要求：

题目如下：

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1：
输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。
示例 2：
输入：nums = [0,1,0,3,2,3]
输出：4
示例 3：
输入：nums = [7,7,7,7,7,7,7]
输出：1
提示：
1 <= nums.length <= 2500
- <= nums[i] <=
进阶：
你能将算法的时间复杂度降低到 O(n log(n)) 吗?

代码框架已经提供如下：

class Solution(object):
def lengthOfLIS(self, nums):
"""
:type nums: List[int]
:rtype: int
"""

2.结果代码：

import bisectclass Solution(object):def lengthOfLIS(self, nums):""":type nums: List[int]:rtype: int"""if not nums:return 0tails = []                  # tails[i] 代表长度为 i+1 的 LIS 的最小末尾元素for x in nums:# 在 tails 中找到第一个 >= x 的位置idx = bisect.bisect_left(tails, x)if idx == len(tails):   # x 比 tails 中所有元素都大tails.append(x)else:                   # 否则替换以保持 tails 递增且最小tails[idx] = xreturn len(tails)

说明：

这个算法之所以这样选择，在于它把「求最长递增子序列的长度」转化成了一个看似无关的「维护一个尽可能小的单调数组 tails」。

1.为什么只关心“长度”就可以忘掉所有序列细节

题目只要长度，不要真正的子序列。
因此，我们不在乎 某个长度对应的具体序列是什么，
只在乎 “长度为 k 的递增子序列能取到的最小末尾值”。
只要这个末尾值越小，后面就有越大机会继续延长。
把这一观察形式化：
tails[k] = “所有长度为 k+1 的递增子序列中，最后一个元素的最小值”

2.tails 数组天然单调递增
反证：
假设存在 i < j，但 tails[i] ≥ tails[j]。
那么长度为 j+1 的子序列至少要包含 j+1 个数，
而它的最后一个数 tails[j] 却比 tails[i] 小或相等。
此时把前 j 个数截掉后 i+1 个数仍然递增且最后一个数 ≤ tails[j] ≤ tails[i]，
于是我们能用更小的末尾值得到一个长度为 i+1 的子序列，
这与 tails[i] 的“最小”定义矛盾。
所以 tails 必严格单调递增。

有了这个单调性，就可以用 二分查找 在 O(log n) 时间内定位插入位置。

3.算法流程的细节
遍历数组时，对每一个元素 x：

如果 x 比 tails 里所有数都大 → 直接 append，
相当于“找到一条更长的递增子序列”。
否则，用 x 替换掉 第一个 ≥ x 的位置 上的值。
这一步不是随意替换，而是 在保证长度不变的前提下把末尾值变小，
从而给后面的数字更多“可接龙”的机会。
虽然替换后旧序列被“破坏”，但长度信息被完美保留在 tails 的大小里。

由于 tails 始终保持“最小末尾”的性质，
遍历结束时它的长度就是全局最长递增子序列的长度。

一句话总结：
把“最长递增子序列”这一看似需要回溯所有可能组合的问题，压缩成 只维护一个单调数组 tails 的长度，并用二分查找在每一步 O(log n) 时间内完成更新~

题目2：乘积最大子数组

1.题目要求：

题目如下：

给你一个整数数组 nums ，请你找出数组中乘积最大的非空连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。
测试用例的答案是一个 32-位 整数。
示例 1:
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
提示:
1 <= nums.length <= 2 *
-10 <= nums[i] <= 10
nums 的任何子数组的乘积都保证是一个 32-位 整数

代码框架已经提供如下：

class Solution(object):
def maxProduct(self, nums):
"""
:type nums: List[int]
:rtype: int
"""

2.结果代码：

class Solution(object):def maxProduct(self, nums):""":type nums: List[int]:rtype: int"""if not nums:return 0max_prod = nums[0]          # 全局答案imax = imin = nums[0]       # 以当前元素结尾的最大/最小乘积for x in nums[1:]:# 如果 x 为负数，imax 与 imin 会互换if x < 0:imax, imin = imin, imaximax = max(x, imax * x)  # 要么自成一段，要么接在前一段后面imin = min(x, imin * x)  # 同理max_prod = max(max_prod, imax)return max_prod

说明：

乘积类 DP 的典型特征：
负数 × 负数会变成正数，因此必须同时记住“以 i 结尾的最大乘积”和“最小乘积”。
一次遍历即可，时间 O(n)、空间 O(1)。

题目3：分割等和子集

1.题目要求：

题目如下：

给你一个 只包含正整数 的非空数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。
示例 1：
输入：nums = [1,5,11,5]
输出：true
解释：数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2：
输入：nums = [1,2,3,5]
输出：false
解释：数组不能分割成两个元素和相等的子集。
提示：
1 <= nums.length <= 200
1 <= nums[i] <= 100

代码框架已经提供如下：

class Solution(object):
def canPartition(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""

2.结果代码：

class Solution(object):def canPartition(self, nums):""":type nums: List[int]:rtype: bool"""total = sum(nums)if total & 1:                 # 总和为奇数，不可能平分return Falsetarget = total // 2n = len(nums)# 一维滚动数组dp = [False] * (target + 1)dp[0] = True                  # 和为 0 总可以for num in nums:# 倒序更新，防止重复选取for s in range(target, num - 1, -1):dp[s] = dp[s] or dp[s - num]return dp[target]

说明：

经典 01 背包 判定：
把问题转化为「能否从数组中选出若干数，使其和为总和的一半」。
若总和为奇数，直接 False；否则做背包即可。

时间：O(n·target) ≈ O(200×10^4) 在 Python 中毫无压力。
空间：O(target)。

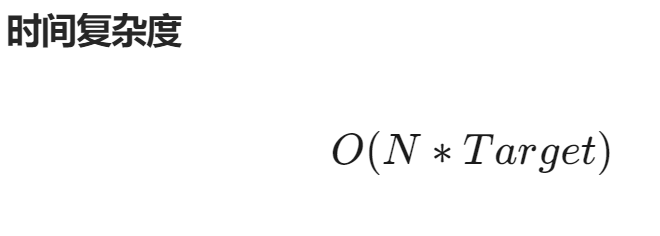
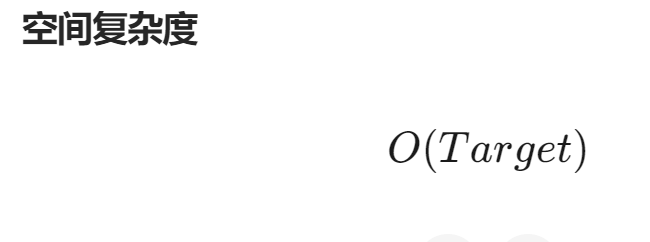
题目4：最长有效括号

1.题目要求：

题目如下：

给你一个只包含 '(' 和 ')' 的字符串，找出最长有效（格式正确且连续）括号子串的长度。
左右括号匹配，即每个左括号都有对应的右括号将其闭合的字符串是格式正确的，比如 "(()())"。
示例 1：
输入：s = "(()"
输出：2
解释：最长有效括号子串是 "()"
示例 2：
输入：s = ")()())"
输出：4
解释：最长有效括号子串是 "()()"
示例 3：
输入：s = ""
输出：0
提示：
0 <= s.length <= 3 *
s[i] 为 '(' 或 ')'

代码框架已经提供如下：

class Solution(object):
def longestValidParentheses(self, s):
"""
:type s: str
:rtype: int
"""

2.结果代码：

class Solution(object):def longestValidParentheses(self, s):""":type s: str:rtype: int"""stack = [-1]          # 栈底哨兵，方便计算长度max_len = 0for i, ch in enumerate(s):if ch == '(':stack.append(i)else:  # ch == ')'stack.pop()if not stack:           # 弹空说明当前右括号无法匹配stack.append(i)     # 作为新的哨兵else:                   # 匹配成功max_len = max(max_len, i - stack[-1])return max_len

说明：

思路（一次遍历 + 栈）：

把「有效括号子串的长度」转化为「两个合法括号之间的索引差」。
维护一个栈，栈底始终放最近一个未匹配左括号的前一个索引，这样每次匹配成功时，栈顶元素就是当前有效子串的起点的前一个位置，长度直接 i - stack[-1] 即可。