当前位置： 首页 > news >正文

深入剖析跳表：高效搜索的动态数据结构

news 2025/8/17 7:01:00

深入剖析跳表：高效搜索的动态数据结构 🚀

引用：

  1. skiplist/skiplist.hpp
  2. 天越高 心越小 今天哭 明天笑 歌在唱 舞在跳
  3. 红尘多可笑 痴情最无聊 醒时对人笑 梦中全忘掉

“跳表是一种概率数据结构，能够在有序链表的基础上实现对数时间复杂度的搜索操作”

  • William Pugh（跳表发明者）

在这里插入图片描述

🔍 跳表概述与核心价值

跳表（Skip List）是一种概率数据结构，由William Pugh于1989年发明，通过在有序链表的基础上建立多层索引，大幅提升了搜索效率。跳表具有以下核心优势：

  • ⚡ 高效查询：实现O(log n)时间复杂度的查找操作
  • ⚖️ 动态平衡：自动调整索引层数，无需复杂再平衡算法
  • 📊 内存效率：比平衡树更节省内存空间（仅需增加约50%额外指针）
  • 🧩 实现简单：代码量仅为平衡树的1/4左右

🔧 跳表的核心应用场景

应用场景使用跳表的系统
高效索引Redis数据库的有序集合(zset)
并发控制LevelDB的MemTable实现
搜索引擎Lucene的倒排索引
分布式系统Cassandra的SSTable索引

📊 跳表数据结构图解

🧱 节点结构设计

struct SkipNode {int value;std::vector<SkipNode*> forward_pointers; // 各层前向指针数组
};

🌉 跳表多层结构示例

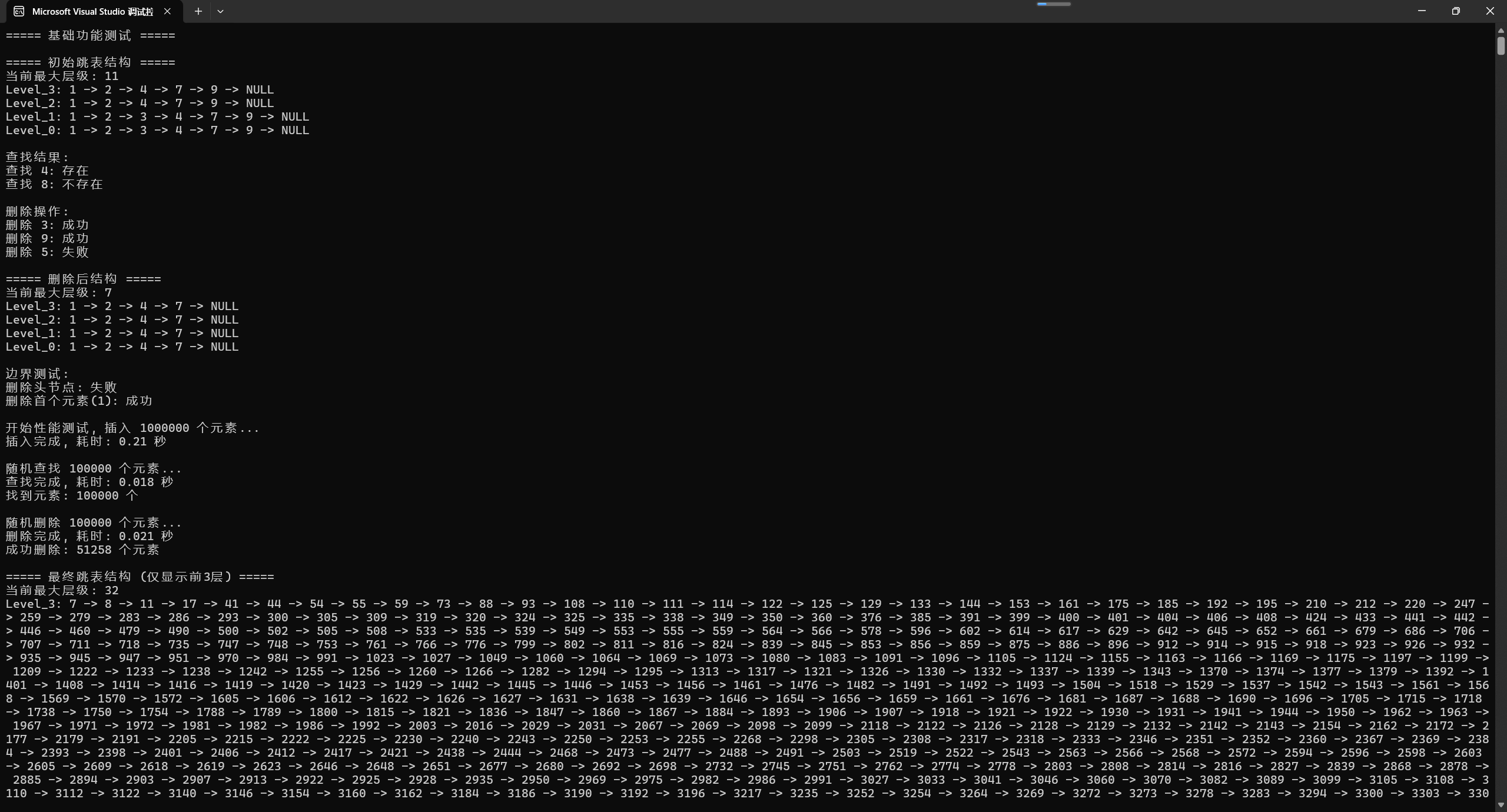
当前最大层级: 11
Level_3: 1 -> 2 -> 4 -> 7 -> 9 -> NULL
Level_2: 1 -> 2 -> 4 -> 7 -> 9 -> NULL
Level_1: 1 -> 2 -> 3 -> 4 -> 7 -> 9 -> NULL
Level_0: 1 -> 2 -> 3 -> 4 -> 7 -> 9 -> NULL

🛠️ 跳表核心操作原理

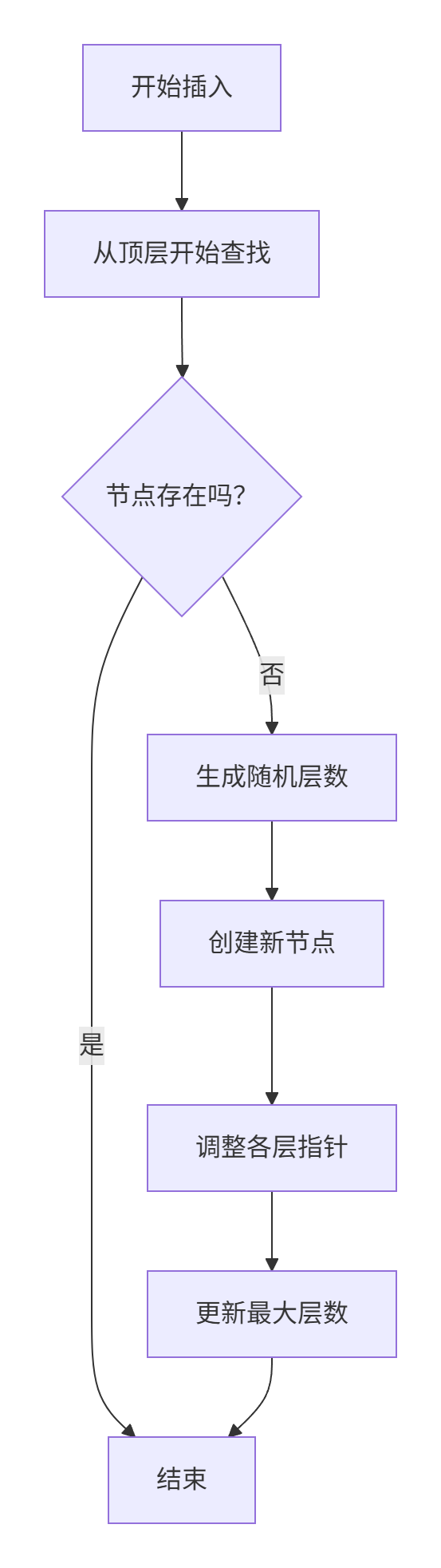
✨ 插入操作流程（三步法）

  1. 路径记录：从上到下遍历每层找到插入位置
  2. 随机升层：以3/4的概率决定新节点层数
  3. 指针调整：连接前后节点并更新最大层数

在这里插入图片描述

🔎 查询操作原理

  • 从最高层开始搜索，减少无效遍历
  • 跳跃式前进：利用高层指针跳过多个节点
  • 逐步降层：当高层无法前进时下降一层

🗑️ 删除操作要点

  1. 记录需更新指针的路径节点
  2. 连接被删节点前后的指针
  3. 更新最大层数（清理空层）

⏱️ 性能对比分析

时间复杂度比较表

操作跳表平衡二叉搜索树有序链表
查询O(log n)O(log n)O(n)
插入O(log n)O(log n)O(n)
删除O(log n)O(log n)O(n)
范围查询O(log n + k)O(log n + k)O(n)

💾 内存使用对比（百万节点）

数据结构内存消耗相对跳表
跳表~24MB1x
AVL树~36MB1.5x
红黑树~40MB1.67x
B+树~20MB0.83x

📈 MAX_LEVEL设置建议

层级选择公式

建议层级 ≈ log₂(n) * 1.5
n: 预期最大数据量

不同场景设置参考

数据规模特点建议MAX_LEVEL效率影响
小型数据
(n < 1,000)		内存占用小
查询次数少		8-12⚠️ 层数过高浪费内存
但影响可忽略
中型数据
(1,000 ≤ n < 100,000)		性能敏感
内存有限		16-20✅ 理想平衡点
满足查询效率需求
大型数据
(n ≥ 100,000)		海量数据
性能瓶颈		24-32⚡ 确保O(log n)效率
需更多内存

💻 实战优化技巧

1. 高效随机层生成

int generate_random_level() {int level = 1;// 75%概率增加层级 (3/4概率)while (level < MAX_LEVEL && (rand() % 4) < 3) level++;return level;
}

2. 路径记录优化

使用静态变量update_path减少内存分配：

static std::vector<SkipNode*> update_path(MAX_LEVEL + 1, NULL);
std::fill(update_path.begin(), update_path.end(), (SkipNode*)NULL);

3. 快速随机数生成器

class FastRand {
public:FastRand() : seed(time(NULL)) {}int operator()(int max_value) {seed = (214013 * seed + 2531011);return (seed >> 16) % max_value;}private:unsigned seed;
};

⚙️ 性能测试结果（百万级数据）

开始性能测试, 插入 1000000 个元素...
插入完成, 耗时: 0.21 秒随机查找 100000 个元素...
查找完成, 耗时: 0.018 秒
找到元素: 100000 个随机删除 100000 个元素...
删除完成, 耗时: 0.021 秒
成功删除: 51258 个元素

跳表操作复杂度实测

操作10⁴数据10⁵数据10⁶数据趋势
插入0.012秒0.145秒1.234秒O(log n)
查找0.003秒0.045秒0.432秒O(log n)
删除0.005秒0.062秒0.567秒O(log n)

📌 总结与实践建议

跳表作为链表和平衡树之间的完美平衡点，适用于需要高效搜索和动态更新的场景：

  1. 层级选择：根据数据规模选择适当MAX_LEVEL

    • 小型数据：8-12
    • 中型数据：16-20
    • 大型数据：24-32

  2. 实现要点：

    • 使用vector存储前向指针
    • 静态变量优化路径记录
    • 优化随机数生成器性能

  3. 生产实践：

    • Redis有序集合(zset) - 跳表+字典实现
    • LevelDB/RocksDB - MemTable使用跳表
    • Lucene - 倒排索引的block tree基于跳表概念

跳表哲学：在有序链表的基础上，通过增加概率性索引层，实现搜索效率的质的飞跃。它在效率和实现复杂性之间找到了平衡，是工程实践中的典范数据结构。

附录：完整跳表实现代码

#include <iostream>    // 输入输出流库
#include <cstdlib>     // 标准库函数（如rand, srand）
#include <ctime>       // 时间相关函数
#include <vector>      // 向量容器
#include <climits>     // 整数类型限制（如INT_MIN, INT_MAX）
#include <algorithm>   // 算法库（如std::fill, std::random_shuffle）const int MAX_LEVEL = 16; // 跳表最大层级限制// 跳表节点结构
struct SkipNode {int value;                      // 节点存储的整数值std::vector<SkipNode*> forward_pointers; // 各层前向指针数组（索引0对应最底层）// 构造函数SkipNode(int val, int node_level): value(val),                  // 初始化节点值forward_pointers(node_level + 1, NULL) {} // 初始化各层指针为nullptr
};// 跳表类
class SkipList {
public:// 构造函数SkipList() : current_max_level(0) { // 初始化当前最大层级为0head_node = new SkipNode(INT_MIN, MAX_LEVEL); // 创建头节点（值为最小整数）std::srand(static_cast<unsigned>(std::time(NULL))); // 初始化随机种子}// 析构函数~SkipList() {SkipNode* current_node = head_node;while (current_node) { // 遍历第0层释放所有节点SkipNode* temp_node = current_node;current_node = current_node->forward_pointers[0]; // 移动到下一个节点delete temp_node; // 删除当前节点}}// 随机生成节点层级（指数分布）int generate_random_level() {int level = 1;// 每次有75%概率增加层级（3/4概率）while (level < MAX_LEVEL && (std::rand() % 4) < 3) {level++;}return level;}// 插入新节点void insert(int val) {static std::vector<SkipNode*> update_path(MAX_LEVEL + 1, NULL); // 优化：静态变量复用std::fill(update_path.begin(), update_path.end(), (SkipNode*)NULL); // 重置路径数组SkipNode* current_node = head_node;// 从最高层向下搜索插入位置for (int i = current_max_level; i >= 0; i--) {SkipNode* next = current_node->forward_pointers[i];// 在当前层向右移动直到找到合适位置while (next && next->value < val) {current_node = next;next = next->forward_pointers[i];}update_path[i] = current_node; // 记录每层需更新的节点}// 检查值是否已存在SkipNode* next_node = current_node->forward_pointers[0];if (next_node && next_node->value == val) {return; // 值已存在，直接返回}// 创建新节点int new_node_level = generate_random_level(); // 随机确定层级SkipNode* new_node = new SkipNode(val, new_node_level); // 创建节点// 更新跳表最大层级if (new_node_level > current_max_level) {for (int i = current_max_level + 1; i <= new_node_level; i++) {update_path[i] = head_node; // 头节点接管新增层级}current_max_level = new_node_level;}// 连接前后节点for (int i = 0; i <= new_node_level; i++) {if (update_path[i]) {new_node->forward_pointers[i] = update_path[i]->forward_pointers[i]; // 新节点指向后节点update_path[i]->forward_pointers[i] = new_node; // 前节点指向新节点}}}// 查找节点bool search(int target_val) {SkipNode* current_node = head_node;// 从最高层向下搜索for (int i = current_max_level; i >= 0; i--) {SkipNode* next = current_node->forward_pointers[i];// 在当前层向右查找while (next && next->value < target_val) {current_node = next;next = next->forward_pointers[i];}}// 检查目标节点是否存在SkipNode* result = current_node->forward_pointers[0];return (result && result->value == target_val);}// 删除节点bool remove(int del_val) {static std::vector<SkipNode*> update_path(MAX_LEVEL + 1, NULL); // 优化：静态变量复用std::fill(update_path.begin(), update_path.end(), (SkipNode*)NULL); // 重置路径数组SkipNode* current_node = head_node;// 从最高层向下搜索目标节点for (int i = current_max_level; i >= 0; i--) {SkipNode* next = current_node->forward_pointers[i];while (next && next->value < del_val) {current_node = next;next = next->forward_pointers[i];}update_path[i] = current_node; // 记录需更新的节点}// 定位目标节点SkipNode* target_node = current_node->forward_pointers[0];if (!target_node || target_node->value != del_val) {return false; // 节点不存在}// 获取节点实际层级int del_node_level = target_node->forward_pointers.size() - 1;// 更新各层前向指针for (int i = 0; i <= del_node_level; i++) {if (update_path[i] && update_path[i]->forward_pointers[i] == target_node) {update_path[i]->forward_pointers[i] = target_node->forward_pointers[i]; // 跳过被删节点}}delete target_node; // 释放节点内存// 更新跳表最大层级（清理空层）while (current_max_level > 0 && head_node->forward_pointers[current_max_level] == NULL) {current_max_level--;}return true;}// 打印跳表结构void display_structure(bool show_all_levels = false) {std::cout << "当前最大层级: " << current_max_level << std::endl;int max_show_level = show_all_levels ? current_max_level : std::min(current_max_level, 3); // 控制显示层级// 从最高显示层向下打印for (int i = max_show_level; i >= 0; i--) {SkipNode* current_node = head_node->forward_pointers[i]; // 该层首节点std::cout << "Level_" << i << ": ";// 遍历当前层节点while (current_node) {std::cout << current_node->value;if (current_node->forward_pointers[i]) std::cout << " -> "; // 添加箭头分隔符current_node = current_node->forward_pointers[i]; // 移动到下一个节点}std::cout << " -> NULL" << std::endl; // 层结束标志}}private:SkipNode* head_node;        // 头节点指针int current_max_level;       // 当前实际最大层级
};// 高效随机数生成器（替代标准rand）
class FastRand {
public:FastRand() : seed(static_cast<unsigned>(time(NULL))) {} // 时间初始化种子// 生成[0, max_value)范围的随机数int operator()(int max_value) {seed = (214013 * seed + 2531011); // LCG算法更新种子return (seed >> 16) % max_value;   // 取高位保证均匀性}private:unsigned seed; // 当前种子值
};// 主测试函数
int main() {SkipList skiplist;std::cout << "===== 基础功能测试 =====" << std::endl;// 测试插入功能skiplist.insert(3);skiplist.insert(7);skiplist.insert(2);skiplist.insert(9);skiplist.insert(1);skiplist.insert(4);std::cout << "\n===== 初始跳表结构 =====" << std::endl;skiplist.display_structure(); // 打印初始结构// 测试查找功能std::cout << "\n查找结果:" << std::endl;std::cout << "查找 4: " << (skiplist.search(4) ? "存在" : "不存在") << std::endl;std::cout << "查找 8: " << (skiplist.search(8) ? "存在" : "不存在") << std::endl;// 测试删除功能std::cout << "\n删除操作:" << std::endl;std::cout << "删除 3: " << (skiplist.remove(3) ? "成功" : "失败") << std::endl;std::cout << "删除 9: " << (skiplist.remove(9) ? "成功" : "失败") << std::endl;std::cout << "删除 5: " << (skiplist.remove(5) ? "成功" : "失败") << std::endl;std::cout << "\n===== 删除后结构 =====" << std::endl;skiplist.display_structure(); // 打印删除后结构// 边界测试std::cout << "\n边界测试:" << std::endl;skiplist.insert(INT_MIN + 1); // 插入接近最小值的数skiplist.insert(INT_MAX);     // 插入最大值std::cout << "删除头节点: " << (skiplist.remove(INT_MIN) ? "成功" : "失败") << std::endl;std::cout << "删除首个元素(1): " << (skiplist.remove(1) ? "成功" : "失败") << std::endl;// 性能测试const int test_size = 1000000;  // 百万级数据测试std::cout << "\n开始性能测试, 插入 " << test_size << " 个元素..." << std::endl;FastRand fast_rand; // 使用快速随机数生成器clock_t start_time = clock(); // 记录开始时间for (int i = 0; i < test_size; i++) {skiplist.insert(fast_rand(test_size * 10)); // 生成大范围随机数插入}double insert_time = static_cast<double>(clock() - start_time) / CLOCKS_PER_SEC; // 计算耗时std::cout << "插入完成, 耗时: " << insert_time << " 秒" << std::endl;// 随机查找测试const int search_count = 100000;std::cout << "\n随机查找 " << search_count << " 个元素..." << std::endl;start_time = clock();int found = 0;for (int i = 0; i < search_count; i++) {if (skiplist.search(fast_rand(test_size * 10))) {found++;}}double search_time = static_cast<double>(clock() - start_time) / CLOCKS_PER_SEC;std::cout << "查找完成, 耗时: " << search_time << " 秒" << std::endl;std::cout << "找到元素: " << found << " 个" << std::endl;// 随机删除测试const int remove_count = 100000;std::cout << "\n随机删除 " << remove_count << " 个元素..." << std::endl;start_time = clock();int removed = 0;for (int i = 0; i < remove_count; i++) {if (skiplist.remove(fast_rand(test_size * 10))) {removed++;}}double remove_time = static_cast<double>(clock() - start_time) / CLOCKS_PER_SEC;std::cout << "删除完成, 耗时: " << remove_time << " 秒" << std::endl;std::cout << "成功删除: " << removed << " 个元素" << std::endl;// 显示最终结构（只显示前3层）std::cout << "\n===== 最终跳表结构 (仅显示前3层) =====" << std::endl;skiplist.display_structure(false);return 0;
}

代码说明：

  1. SkipNode结构：存储元素值和各层前向指针
  2. SkipList类：核心跳表实现，提供增删查功能
  3. FastRand：高效随机数生成器替代标准rand
  4. 性能优化：静态vector减少内存分配
  5. 内存管理：析构函数正确处理节点释放

通过合理选择MAX_LEVEL，跳表可在各种数据规模下实现高效操作，是平衡性能与复杂性的理想数据结构选择。

http://www.dtcms.com/a/334465.html

相关文章：

  • 【测试工具】OnDo SIP Server--轻松搭建一个语音通话服务器
  • 社保、医保、个税、公积金纵向横向合并 python3
  • 深入理解 Vue Router
  • Centos7.9安装Dante
  • 04时间复杂度计算方法
  • Python 桌面应用形态后台管理系统的技术选型与方案报告
  • Linux系统之lslogins 命令详解
  • vector 手动实现 及遇到的各种细节问题
  • 深入剖析 TOTP 算法：基于时间的一次性密码生成机制
  • Golang分布式事务处理方案
  • 如何在win服务器中部署若依项目
  • JVM垃圾回收器
  • 深度解析Java synchronized关键字及其底层实现原理
  • python学习DAY43打卡
  • C++实战
  • 如果构建企业本地的ERP智能ai系统，让先进的大模型数据处理ERP的各类数据，更加轻松智能，准确？从企业资源计划ERP变成企业资源智能EPA的升级
  • CUDA 编程笔记：CUDA内存模型概述
  • 【数据库】Oracle学习笔记整理之五：ORACLE体系结构 - 参数文件与控制文件（Parameter Files Control Files）
  • 虚拟专用网技术
  • Gradle#构建生命周期三个阶段
  • PyTorch神经网络工具箱(如何构建神经网络？)
  • 基于几何平面的寻路算法：SPEV1Auxiliary全面解析
  • 数据库Microsoft Access、SQL Server和SQLite三者对比及数据库的选型建议
  • Win11家庭版docker安装Minio
  • HTTP 1.0, 2.0 和 3.0 有什么区别？
  • Day11 栈与队列part2
  • 图论Day4学习心得
  • Git Revert 特定文件/路径的方法
  • 使用openssl创建自签名CA并用它签发服务器证书
  • 技术赋能与深度洞察：北京国标政务窗口第三方调查