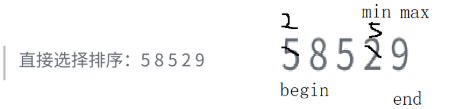【数据结构初阶】--排序(五):计数排序,排序算法复杂度对比和稳定性分析
😘个人主页:@Cx330❀
👀个人简介:一个正在努力奋斗逆天改命的二本觉悟生
📖个人专栏:《C语言》《LeetCode刷题集》《数据结构-初阶》
前言:今天这篇博客就给大家将一个计数排序,然乎就给大家总结一下所有的排序算法的时间复杂度,空间复杂度,稳定性进行一个归纳总结。
目录
一、计数排序
核心步骤:
代码实现:
测试结果:
计数排序的特性:
二.排序算法复杂度及稳定性分析
各排序算法对比表:
代码展现:
Sort.c:
Sort.h:
test.c:
一、计数排序
- 统计相同元素出现次数
- 根据统计的结果将序列回收到原来的序列中
核心步骤:
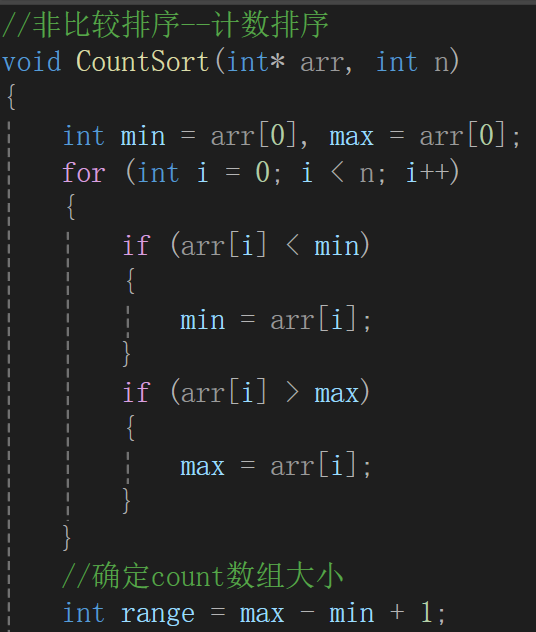
1. 确定数据范围
遍历数组,找到最大值和最小值,然后计算数据范围range=max-min+1确定数组的空间(避免空间浪费)
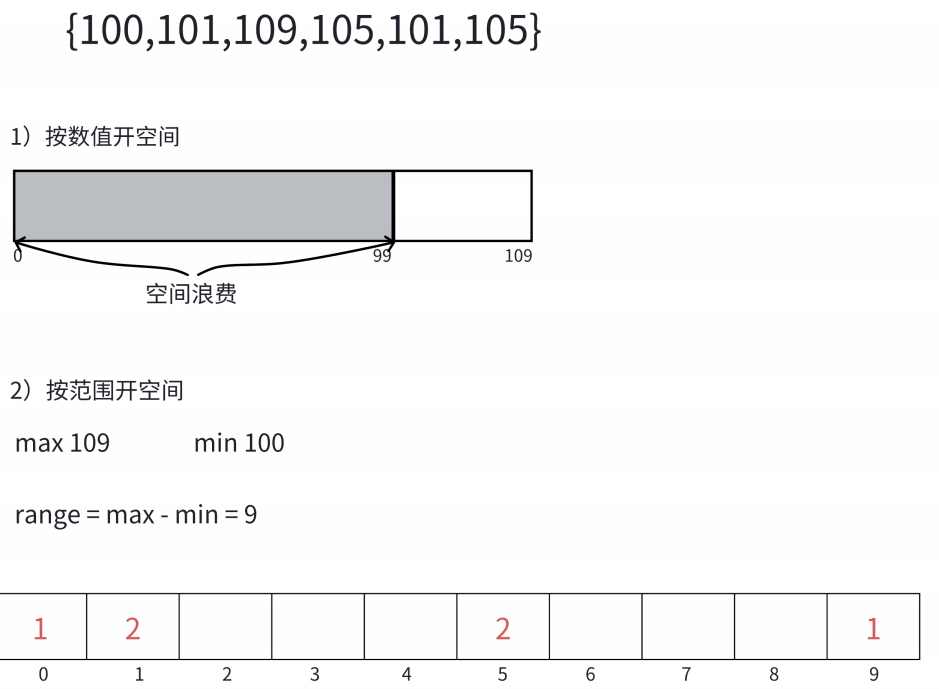
2. 统计元素出现次数
创建一个计数数组count,空间大小为range,并且要给count初始化(calloc或者memset),遍历原数组,将每个元素 arr[i] 映射到 count[arr[i] - min](减去 min 是为了处理包含负数的情况,一定要用arr[i]-min),统计每个值的出现次数。

3. 将count数组中的数据排序还原到原数组中
再定义一个index变量,作为原数组的下标,遍历count数组,根据count[i]统计到的个数进行映射i+min就是原数组的值,循环次数等于该值出现的次数,将数组的原始数据值放入arr原始数组中(对应原始值一定是i+min)

代码实现:
//非比较排序--计数排序
void CountSort(int* arr, int n)
{int min = arr[0], max = arr[0];for (int i = 0; i < n; i++){if (arr[i] < min){min = arr[i];}if (arr[i] > max){max = arr[i];}}//确定count数组大小int range = max - min + 1;int* count = (int*)malloc(sizeof(int) * range);if (count == NULL){perror("malloc fail!");exit(1);}//对count初始化memset(count, 0, sizeof(int) * range);for (int i = 0; i < n; i++){count[arr[i] - min]++;}//将count数组映射到arr数组中int index = 0;for (int i = 0; i < range; i++){while (count[i]--){arr[index++] = i + min ;}}
}test.c:
#include"Sort.h"
void printArr(int* arr, int n)
{for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}void test01()
{int a[] = { 5,3,9,6,2,4,7,1,8 };//int a[] = { 6,1,2,7,9,3 };int n = sizeof(a) / sizeof(a[0]);printf("排序之前:");printArr(a, n);//InsertSort(a, n);//ShellSort(a, n);//SelectSort(a, n);//HeapSort(a, n);//BubbleSort(a, n);//QuickSort(a, 0, n - 1);//QuickSortNorR(a, 0, n - 1);//MergeSort(a, n);CountSort(a, n);//MergeSortNonR(a, n);printf("排序之后:");printArr(a, n);
}void TestOP()
{srand(time(0));const int N = 100000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();SelectSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();int begin5 = clock();QuickSort(a5, 0, N - 1);int end5 = clock();int begin6 = clock();MergeSort(a6, N);int end6 = clock();int begin7 = clock();BubbleSort(a7, N);int end7 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);printf("SelectSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);printf("QuickSort:%d\n", end5 - begin5);printf("MergeSort:%d\n", end6 - begin6);printf("BubbleSort:%d\n", end7 - begin7);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7);
}int main()
{test01();//TestOP();return 0;
}测试结果:

测试完成,打印没有问题,升序排序正确,退出码为0
计数排序的特性:
- 计数排序在数据范围集中时,效率很高,但是适用范围以及场景有限
- 时间复杂度:O(n+range)
- 空间复杂度:O(range)
- 稳定性:稳定
二.排序算法复杂度及稳定性分析
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
各排序算法对比表:
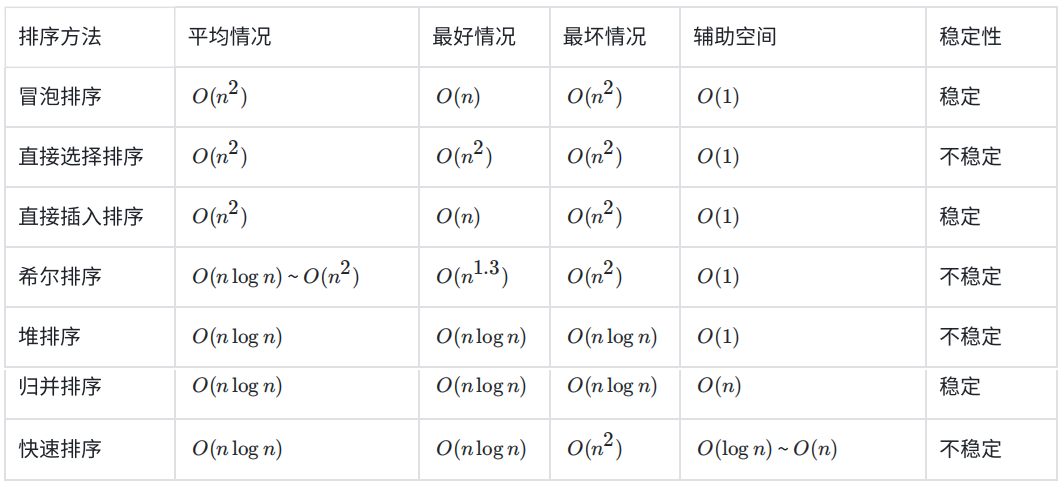
其中冒泡排序,直接插入排序,归并排序是稳定的,这里就不过多介绍了,我们主要通过一些特例来看下那些不稳定的排序算法。至于时间复杂度和空间复杂度,博主大部分都在前面的博客中分享过了。
1.直接选择排序:
2.希尔排序:
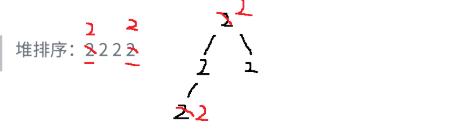
3.堆排序:
4.快速排序:
代码展现:
Sort.c:
#include"Sort.h"
#include"stack.h"
//1)直接插入排序
void InsertSort(int* arr, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = arr[end + 1];while (end >= 0){if (arr[end] > tmp){arr[end + 1] = arr[end];end--;}else{break;}}arr[end + 1] = tmp;}
}//2)希尔排序
void ShellSort(int* arr, int n)
{int gap = n;while (gap > 1){gap = gap / 3 + 1;for (int i = 0; i < n - gap; i++){int end = i;int tmp = arr[end + gap];while (end >= 0){if (arr[end] > tmp){arr[end + gap] = arr[end];end-=gap;}else{break;}}arr[end + gap] = tmp;}}
}void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}
//向下调整
void AdjustDown(int* arr, int parent, int n)
{int child = parent * 2 + 1;while (child < n){ //找大的孩子//建大堆 <//建小堆 >if (child + 1 < n && arr[child] < arr[child + 1]){child++;}//孩子和父亲比较//建大堆 <//建小堆 >if (arr[parent] < arr[child]){Swap(&arr[parent], &arr[child]);parent = child;child = parent * 2 + 1;}else{break;}}
}
void HeapSort(int* arr, int n)
{//向下调整算法--建堆 时间复杂度O(n)for (int i = (n - 1 - 1) / 2; i >= 0; i--){AdjustDown(arr, i, n);//因为这里建的是小堆,所以向下调整,就成了降序}//向上调整算法--建堆 时间复杂度O(n*logn)/*for (int i = 0; i < n; i++){AdjustUp(arr, i);}*///n* lognint end = n - 1;while (end > 0)//循环取最后一个元素与顶交换,再向下调整{Swap(&arr[0], &arr[end]);AdjustDown(arr, 0, end);end--;}
}//冒泡排序
void BubbleSort(int* arr, int n)
{int change = 1;for (int i = 0; i < n-1; i++){for (int j = 0; j < n - 1 - i; j++){if (arr[j] > arr[j + 1]){Swap(&arr[j], &arr[j + 1]);change = 0;}}if (change == 1){break;}}
}//1)直接选择排序
//void SelectSort(int* arr, int n)
//{
// for (int i = 0; i < n; i++)
// {
// int mini = i;
// for (int j = i + 1; j < n; j++)
// {
// if (arr[j] < arr[mini])
// {
// mini = j;
// }
// }
// Swap(&arr[mini], &arr[i]);
// }
//}//直接选择排序
void SelectSort(int* arr, int n)
{int begin = 0, end = n - 1;while (begin < end){int mini = begin;int maxi = begin;for (int i = begin+1; i <= end; i++){if (arr[i] < arr[mini]){mini = i;}if (arr[i] > arr[maxi]){maxi = i;}}//交换if (begin == maxi){maxi = mini;}Swap(&arr[begin], &arr[mini]);Swap(&arr[end], &arr[maxi]);begin++;end--;}
}//找基准值--hoare版本
int _QuickSort1(int* arr, int left, int right)
{int keyi = left;left++;while (left <= right){//right从右往左找比基准值小的,如果大于基准值就--while (left <= right && arr[right] > arr[keyi]){--right;}//left从左往右找比基准值大的,如果小于基准值就++while (left <= right && arr[left] < arr[keyi]){++left;}//left和right交换if(left<=right)Swap(&arr[left++], &arr[right--]);}//right位置就是基准值的位置Swap(&arr[right], &arr[keyi]);return right;
}//找基准值--挖坑法
int _QuickSort(int* arr, int left, int right)
{int hole = left;int key = arr[hole];while (left < right){while (left<right && arr[right] > key){right--;}arr[hole] = arr[right];hole = right;while (left < right && arr[left] < key){++left;}arr[hole] = arr[left];hole = left;}arr[hole] = key;return hole;
}//找基准值--lumoto双指针法
int _QuickSort2(int* arr, int left, int right)
{int prev = left, cur = prev + 1;int keyi = left;while (cur < right){if (arr[cur] < arr[keyi] && ++prev != cur){Swap(&arr[cur], &arr[prev]);}++cur;}Swap(&arr[prev], &arr[keyi]);return prev;
}//快速排序
void QuickSort(int* arr, int left, int right)
{if (left >= right){return;}//找基准值keyiint keyi = _QuickSort(arr, left, right); //左序列[left,keyi-1]右序列[keyi+1,right]QuickSort(arr, left, keyi - 1);QuickSort(arr, keyi + 1, right);
}//找基准值非递归版--栈
void QuickSortNorR(int* arr, int left, int right)
{ST st;STInit(&st);STPush(&st, right);STPush(&st, left);while (!STEmpty(&st)){//取栈顶两次int begin = STTop(&st);STPop(&st);int end = STTop(&st);STPop(&st);//[begin,end]--找基准值int keyi = begin;int prev = begin, cur = prev + 1;while (cur <= end){if (arr[cur] < arr[keyi] && ++prev != cur){Swap(&arr[cur], &arr[prev]);}++cur;}Swap(&arr[prev], &arr[keyi]);keyi = prev;if (keyi + 1 < end){STPush(&st, end);STPush(&st, keyi+1);}if (begin < keyi - 1){STPush(&st, keyi - 1);STPush(&st, begin);}}STDesTroy(&st);
}void _MergeSort(int* arr, int left, int right,int*tmp)
{//分解if (left >= right){return;}//根据mid将[left,right]划分为左右两个序列[left,mid] [mid+1,right]int mid = left + (right - left) / 2;_MergeSort(arr, left, mid,tmp);_MergeSort(arr, mid+1, right,tmp);//合并[left,mid] [mid+1,right]int begin1 = left, end1 = mid;int begin2 = mid+1, end2 = right;int index = left;while (begin1 <= end1 && begin2 <= end2){if (arr[begin1] < arr[begin2]){tmp[index++] = arr[begin1++];}else{tmp[index++] = arr[begin2++];}}//要么begin1越界 //要么begin2越界while (begin1 <= end1){tmp[index++] = arr[begin1++];}while (begin2 <= end2){tmp[index++] = arr[begin2++];}for (int i = left; i <= right; i++){arr[i] = tmp[i];}
}//归并排序
void MergeSort(int* arr, int n)
{int* tmp = (int*)malloc(sizeof(int)*n);//[0,n-1]_MergeSort(arr, 0, n - 1,tmp);free(tmp);tmp = NULL;
}//非比较排序--计数排序
void CountSort(int* arr, int n)
{int min = arr[0], max = arr[0];for (int i = 0; i < n; i++){if (arr[i] < min){min = arr[i];}if (arr[i] > max){max = arr[i];}}//确定count数组大小int range = max - min + 1;int* count = (int*)malloc(sizeof(int) * range);if (count == NULL){perror("malloc fail!");exit(1);}//对count初始化memset(count, 0, sizeof(int) * range);for (int i = 0; i < n; i++){count[arr[i] - min]++;}//将count数组映射到arr数组中int index = 0;for (int i = 0; i < range; i++){while (count[i]--){arr[index++] = i + min ;}}
}//归并排序--非递归版本
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail!\n");exit(1);}int gap = 1;while (gap < n){//根据gap划分组,两两合并for (int i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;int index = begin1;//处理奇数个数据if (begin2 >= n){break;}if (end2 >= n){end2 = n - 1;}//合并while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[index++] = a[begin1++];}else{tmp[index++] = a[begin2++];}}while (begin1 <= end1){tmp[index++] = a[begin1++];}while (begin2 <= end2){tmp[index++] = a[begin2++];}//tmp导入到a数组中memcpy(a + i, tmp+i, sizeof(int)*(end2 - i + 1));}gap *= 2;}free(tmp);
}Sort.h:
#include<stdio.h>
#include<stdlib.h>
#include<memory.h>
#include<time.h>
//插入排序
//1)直接插入排序
void InsertSort(int* arr, int n);
//2)希尔排序
void ShellSort(int* arr, int n);//选择排序
//1)直接选择排序
void SelectSort(int* arr, int n);
//2)堆排序
void HeapSort(int* arr, int n);
//冒泡排序
void BubbleSort(int* arr, int n);
//快速排序
void QuickSort(int* arr, int left, int right);
//找基准值非递归版--栈
void QuickSortNorR(int* arr, int left, int right);
//归并排序--递归版本
void MergeSort(int* arr, int n);
//非比较排序--计数排序
void CountSort(int* arr, int n);
//归并排序--非递归版本
void MergeSortNonR(int* a, int n);test.c:
#include"Sort.h"
void printArr(int* arr, int n)
{for (int i = 0; i < n; i++){printf("%d ", arr[i]);}printf("\n");
}void test01()
{int a[] = { 5,3,9,6,2,4,7,1,8 };//int a[] = { 6,1,2,7,9,3 };int n = sizeof(a) / sizeof(a[0]);printf("排序之前:");printArr(a, n);//InsertSort(a, n);//ShellSort(a, n);//SelectSort(a, n);//HeapSort(a, n);//BubbleSort(a, n);//QuickSort(a, 0, n - 1);//QuickSortNorR(a, 0, n - 1);//MergeSort(a, n);CountSort(a, n);//MergeSortNonR(a, n);printf("排序之后:");printArr(a, n);
}void TestOP()
{srand(time(0));const int N = 100000;int* a1 = (int*)malloc(sizeof(int) * N);int* a2 = (int*)malloc(sizeof(int) * N);int* a3 = (int*)malloc(sizeof(int) * N);int* a4 = (int*)malloc(sizeof(int) * N);int* a5 = (int*)malloc(sizeof(int) * N);int* a6 = (int*)malloc(sizeof(int) * N);int* a7 = (int*)malloc(sizeof(int) * N);for (int i = 0; i < N; ++i){a1[i] = rand();a2[i] = a1[i];a3[i] = a1[i];a4[i] = a1[i];a5[i] = a1[i];a6[i] = a1[i];a7[i] = a1[i];}int begin1 = clock();InsertSort(a1, N);int end1 = clock();int begin2 = clock();ShellSort(a2, N);int end2 = clock();int begin3 = clock();SelectSort(a3, N);int end3 = clock();int begin4 = clock();HeapSort(a4, N);int end4 = clock();int begin5 = clock();QuickSort(a5, 0, N - 1);int end5 = clock();int begin6 = clock();MergeSort(a6, N);int end6 = clock();int begin7 = clock();BubbleSort(a7, N);int end7 = clock();printf("InsertSort:%d\n", end1 - begin1);printf("ShellSort:%d\n", end2 - begin2);printf("SelectSort:%d\n", end3 - begin3);printf("HeapSort:%d\n", end4 - begin4);printf("QuickSort:%d\n", end5 - begin5);printf("MergeSort:%d\n", end6 - begin6);printf("BubbleSort:%d\n", end7 - begin7);free(a1);free(a2);free(a3);free(a4);free(a5);free(a6);free(a7);
}int main()
{test01();//TestOP();return 0;
}往期回顾:
【数据结构初阶】--排序(一):直接插入排序,希尔排序
【数据结构初阶】--排序(二):直接选择排序,堆排序
【数据结构初阶】--排序(三):冒泡排序、快速排序
【数据结构初阶】--排序(四):归并排序
总结:这篇博客到此为止,排序的数据结构就已经全部写完了,数据结构初阶也就结束了,后续我还会写一些某些排序的进阶,然后就正式进入C++的学习了。我们数据结构初阶讲这些数据结构都是用C语言实现的,还有些比较难的数据结构在后续C++的学习中我们也会接触到,但是利用C++来实现就方便很多了,如果文章对你有帮助的话,欢迎评论,点赞,收藏加关注,感谢大家的支持。