[Pyro] 基础构件 | 随机性sample | 可学习参数param | 批量处理plate
链接:https://docs.pyro.ai/en/stable/
docs:Pyro
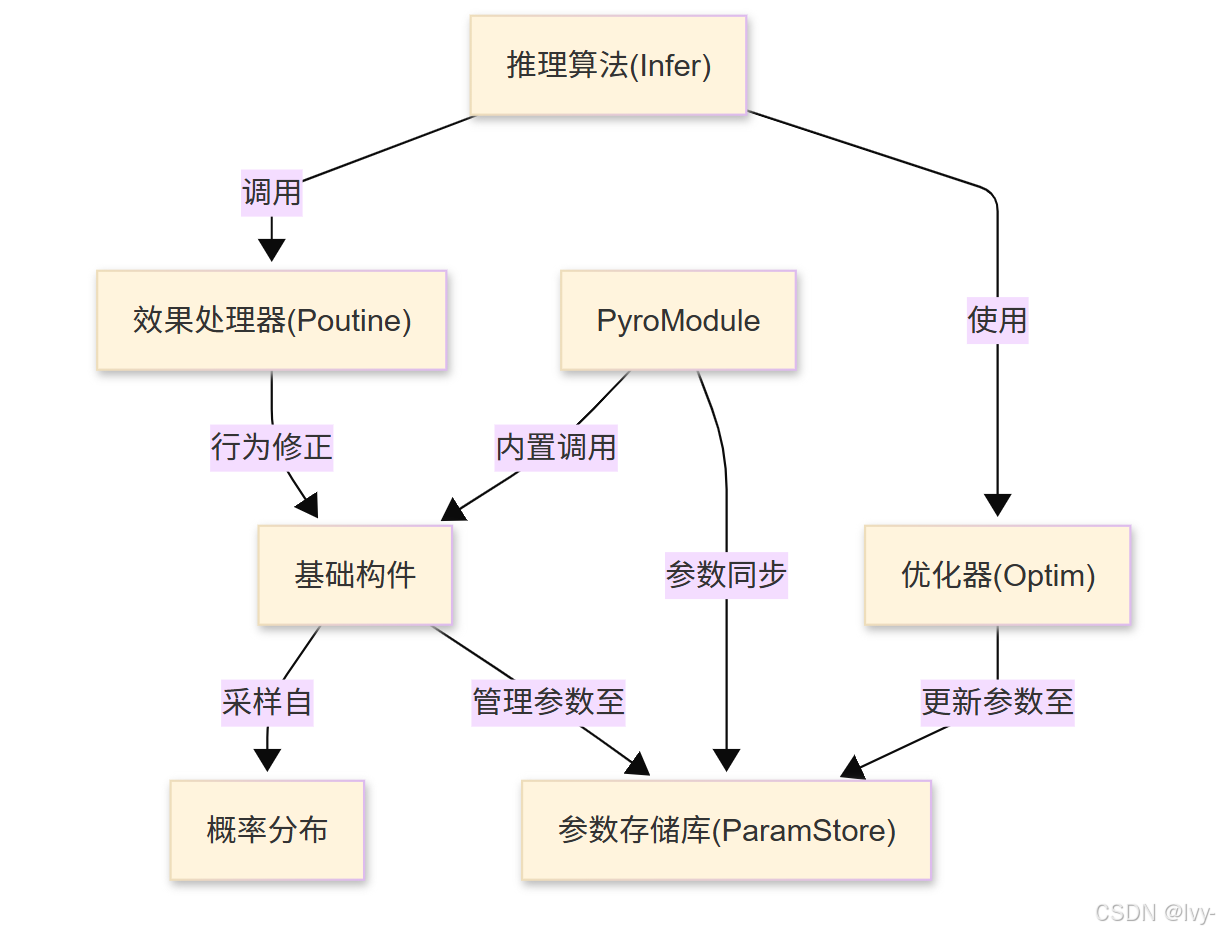
Pyro 是一个基于 PyTorch 构建的**深度概率编程语言**,支持用户构建、组合和学习复杂概率模型。其核心架构包含:
- 基础构件:定义随机变量与可学习参数
- 概率分布:描述不确定性
- 效果处理器(Poutine):动态调整程序行为
- 推理算法:整合SVI与MCMC等优化方法
- 参数存储库:集中管理可学习参数
- PyroModule:实现神经网络与概率模型的无缝集成
架构
章节导航
- 基础构件
- 概率分布
- 参数存储库(ParamStore)
- 效果处理器(Poutine)
- 优化器(Optim)
- 推理算法(Infer)
- PyroModule
第一章:基础构件
欢迎来到Pyro的精彩世界(。・∀・)
在本章中,我们将深入探索构建概率模型的核心机制——“基础构件”。
这些构件如同烹饪食谱中的基础食材,是构建概率世界的基本指令单元。
核心理念
设想我们需要建立计算机模型来模拟不确定性事件
例如咖啡店每小时客流量波动,或根据学习时长预测学生考试通过概率。真实世界的这些现象都具有随机性特征。
构建此类模型需要三个关键步骤:
定义随机事件:“客户数量遵循特定模式的随机分布”声明可学习参数:“客户平均数量可能随时间变化,模型需从数据中自主发现规律”处理事件集合:“拥有多时段的客户数据,各时段客流量相互独立”
这正是Pyro基础构件的核心价值~
这些特殊函数能将上述概念转化为Python代码,构建Pyro可识别并用于学习的"概率程序"。
三大核心构件包括:
pyro.sample:生成随机变量(如"从牌堆抽卡")pyro.param:声明可学习参数(如"调整配方糖量")pyro.plate:声明数据批次的独立性(如"为烤盘每个饼干重复操作")
让我们深入解析每个构件。
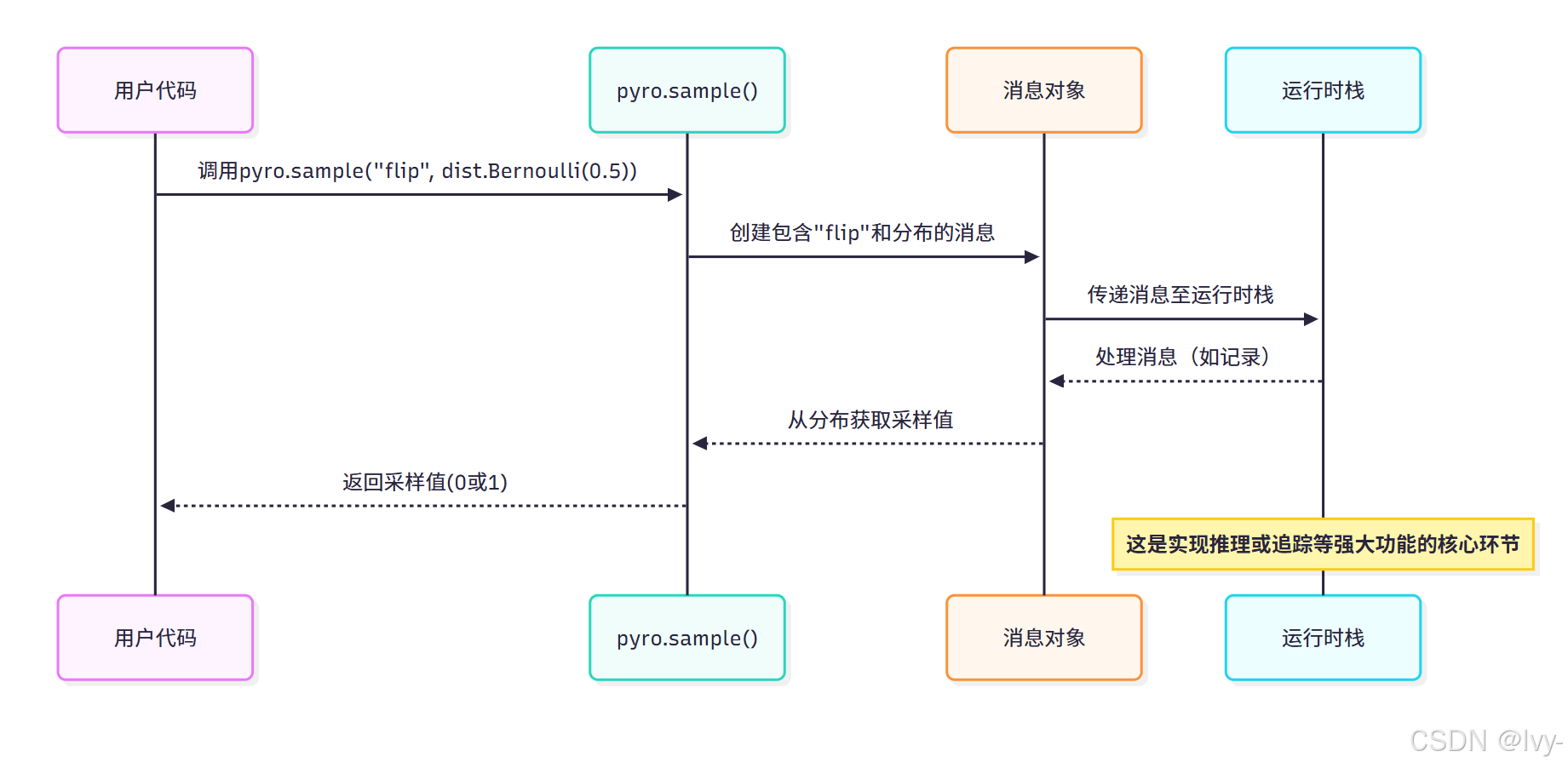
1. pyro.sample:引入随机性
pyro.sample是模型引入随机性的核心方式。使用该构件即告知Pyro:“此处需从指定概率分布抽取随机值”
使用范例
调用pyro.sample时需指定随机变量name和分布对象:
import pyro
import pyro.distributions as dist
import torchdef coin_flip_model():# 定义伯努利分布(类似抛硬币:0反面,1正面)# 设置0.5的正面概率coin_prob = torch.tensor(0.5)# 使用pyro.sample从该分布抽取名为"flip"的随机变量flip = pyro.sample("flip", dist.Bernoulli(coin_prob))return flip# 运行简单模型
outcome = coin_flip_model()
print(f"抛硬币结果: {int(outcome)}")
运行机制:执行coin_flip_model()时,pyro.sample会从Bernoulli(0.5)分布抽取0或1的随机值,每次运行可能获得不同结果,如同真实抛硬币!
底层实现原理
pyro.sample并非简单函数调用,而是创建描述随机事件的"消息对象"(包含名称、分布等信息)。
该消息通过称为"poutine effect handler stack"的内部系统处理(详见Poutine),实现执行过程记录,这对推理算法至关重要。
简化执行流程:
2. pyro.param:声明可学习参数
概率模型常包含需从数据学习的参数。例如模拟偏置硬币时,需根据观测数据学习实际正面概率。
pyro.param正是声明此类可学习参数的核心构件。
使用范例
调用pyro.param需指定参数name和初始值(PyTorch张量),Pyro将自动管理参数优化:
import pyro
import pyro.distributions as dist
import torchdef learnable_coin_model():# 声明名为"coin_bias"的可学习参数# 初始值设为0.5(公平硬币假设)# 参数值将由Pyro存储和更新coin_bias = pyro.param("coin_bias", torch.tensor(0.5, requires_grad=True))# 确保偏置值在[0,1]区间(概率约束)# 使用torch.sigmoid将任意实数映射到[0,1]# 约束与分布的深入解析见[Distributions](02_distributions_.md)constrained_bias = torch.sigmoid(coin_bias)# 基于可学习偏置进行伯努利采样flip = pyro.sample("flip", dist.Bernoulli(constrained_bias))return flip# 运行模型仍会获得随机结果
# 参数学习过程将在后续推理算法中实现
_ = learnable_coin_model()# 访问当前参数值
current_bias = pyro.param("coin_bias")
print(f"当前可学习硬币偏置(初始): {current_bias.item()}")
运行机制:通过pyro.param声明参数后,Pyro将识别其为可优化参数。requires_grad=True是PyTorch标准参数,用于梯度追踪,这对优化过程至关重要。
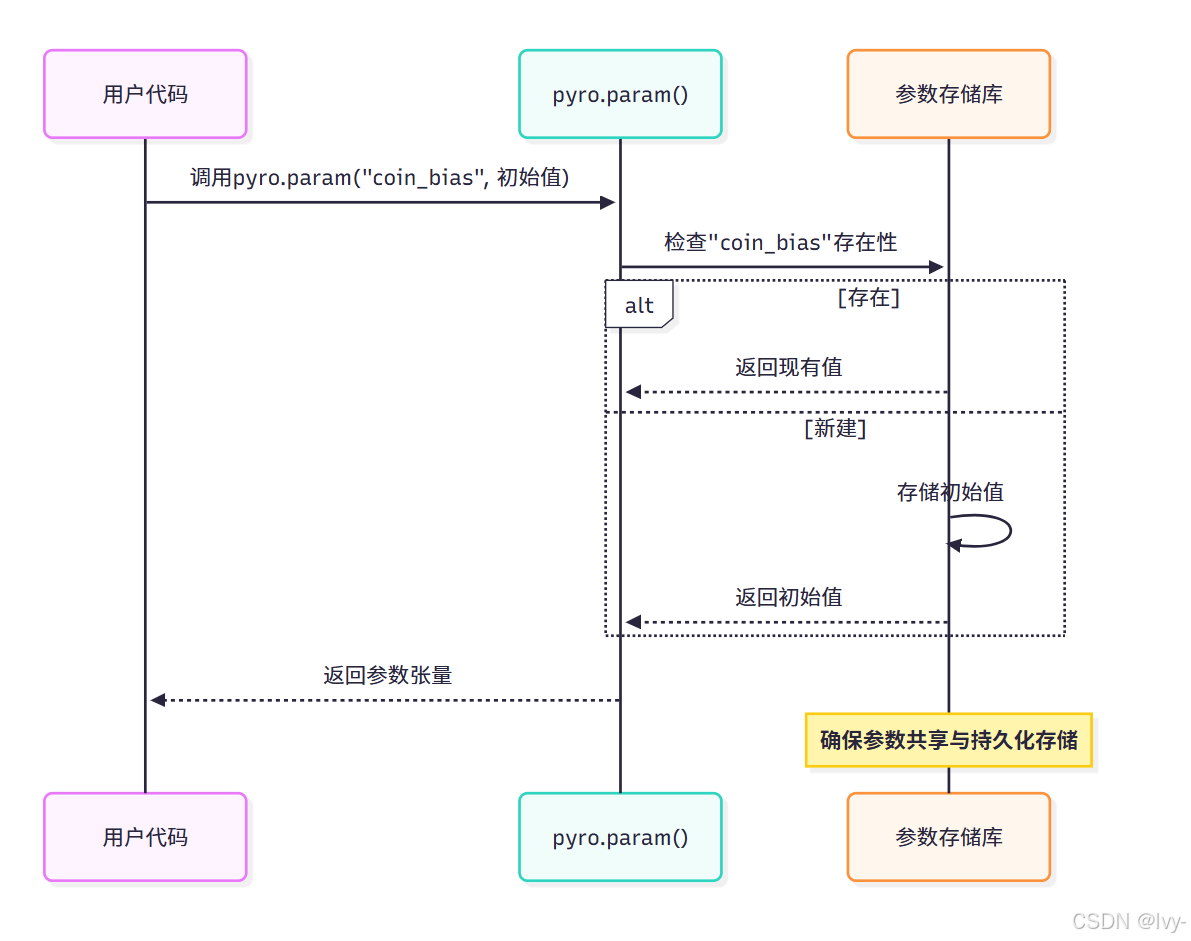
底层实现原理
调用pyro.param时,Pyro会访问全局"参数存储库"。
该存储库类似特殊字典,集中管理所有可学习参数。
-
新参数会被初始化存储
-
已有参数则返回当前值,实现模型不同组件间的参数共享。
详细机制见参数存储库,简化流程:
3. pyro.plate:处理独立性与批次
处理多独立数据点时(如100次抛硬币实验),逐次调用pyro.sample效率低下。pyro.plate通过声明代码块的独立性,支持批量处理。
使用范例
通过上下文管理器使用pyro.plate,指定name、数据总量及可选批次大小:
import pyro
import pyro.distributions as dist
import torchdef hundred_flips_model():# 声明可学习硬币偏置coin_bias = pyro.param("coin_bias", torch.tensor(0.5, requires_grad=True))constrained_bias = torch.sigmoid(coin_bias)# 声明100次独立抛硬币实验# 'data'为唯一标识名# '100'为独立事件总数with pyro.plate("flips_plate", 100):# 该代码块内的pyro.sample调用将视为100次独立采样# 单行代码实现100个独立"flip"采样点flips = pyro.sample("flip", dist.Bernoulli(constrained_bias))# flips将是包含100次结果的张量return flips# 运行模型
all_outcomes = hundred_flips_model()
print(f"100次抛硬币结果维度: {all_outcomes.shape}")
print(f"前10次结果: {all_outcomes[:10].int().tolist()}")
运行机制:pyro.plate实现向量化采样,flips变量成为包含100元素的PyTorch张量,大幅提升大数据集处理效率。
支持子采样处理大规模数据:
import pyro
import pyro.distributions as dist
import torchdef mini_batch_flips_model():coin_bias = pyro.param("coin_bias", torch.tensor(0.5, requires_grad=True))constrained_bias = torch.sigmoid(coin_bias)total_flips = 1000 # 假设总样本量batch_size = 100 # 单次处理100样本# 使用带子采样的pyro.platewith pyro.plate("flips_plate", total_flips, subsample_size=batch_size) as ind:# ind提供当前批次索引print(f"处理批次大小: {len(ind)}")# 模拟大数据集子采样flips_batch = pyro.sample("flip", dist.Bernoulli(constrained_bias).expand([len(ind)]).to_independent(1))# 注:expand和to_independent用于匹配批次维度,暂不需深究# 实际应用中可通过ind索引数据子集print(f"采样批次维度: {flips_batch.shape}")_ = mini_batch_flips_model()
运行机制:带subsample_size的pyro.plate会从1000样本中随机抽取100个索引。
Pyro自动处理概率缩放,确保推理算法正确运作,这对大规模数据处理至关重要。
底层实现原理
pyro.plate通过向运行时栈添加特殊"messenger",通知代码块内的pyro.sample处理批次维度和独立性。当使用子采样时,自动应用缩放因子确保推理正确性。具体实现详见Poutine。
总结
本章解析了Pyro三大基础构件:
| 构件 | 功能定位 | 类比说明 |
|---|---|---|
pyro.sample | 定义随机变量 | 随机抽牌 |
pyro.param | 声明可学习参数 | 调整配方成分 |
pyro.plate | 声明数据批次的独立性 | 批量处理饼干制作步骤 |
这些构件是构建概率模型的核心语言。
通过组合运用,可实现强大灵活的模型构建。
掌握基础构件后,下一步是理解如何描述各类随机现象,这将引导我们进入概率分布的探索。
