当前位置： 首页 > news >正文

扩展卡尔曼滤波EKF、自适应扩展卡尔曼滤波AEKF、HIF/H∞、粒子滤波PF、卡尔曼粒子滤波EKPF在BJDST动态工况下的SOC估计效果

news 2025/8/17 18:11:45

       

        在电动汽车与储能系统中，电池荷电状态（SOC）的精确估计是保障系统安全运行与性能优化的核心环节。然而，实际工况（如BJDST动态循环）中电池模型的强非线性、噪声时变特性及复杂电流波动，对传统估计算法提出了严峻挑战。为应对这一难题，扩展卡尔曼滤波（EKF）通过线性化处理非线性模型，成为经典解决方案；自适应扩展卡尔曼滤波（AEKF）则进一步引入自适应机制，实时调整噪声统计特性，显著提升动态工况下的跟踪精度与鲁棒性。与此同时，H∞滤波（HIF）针对模型不确定性设计，在抗干扰能力上表现突出；粒子滤波（PF）通过蒙特卡洛采样逼近后验概率，适用于强非线性非高斯系统；而卡尔曼粒子滤波（EKPF）则融合EKF与PF优势，以提升状态估计的收敛性与稳定性。本文将详细分析上述算法估计SOC估计的关键代码，为电池管理系统优化提供理论依据与实践参考。

        为了大家可以更好的理解几种不同的算法，接下来在描述原理的时候，同时也使用通俗的例子来解释不同的算法。

1. EKF（扩展卡尔曼滤波）的详细比喻

场景： 想象你是一个手机电池管家，每天要估算手机剩余电量（SOC）。你有一个电池模型（比如：每用1小时，电量下降10%），但你知道这个模型并不完美，因为实际使用中电量下降速度会变化（比如玩游戏时掉电快，待机时掉电慢）。

工作过程：

  • 预测阶段（Predict）：
    你根据当前用电情况（比如当前在玩游戏，每小时掉电15%），预测下一分钟后的电量。比如当前电量是70%，你预测1分钟后电量是69.75%（因为1分钟是1/60小时，15%×1/60=0.25%）。

  • 更新阶段（Update）：
    1分钟后，你查看手机实际显示的电量（通过电压换算得到），发现实际电量是69.8%。你发现预测值（69.75%）和实际值（69.8%）有0.05%的误差。

  • 线性化处理：
    你知道电池的电压和电量关系不是直线（比如电量低时，同样1%电量变化对应的电压变化更大），但你简化处理：在当前电量70%附近，你假设1%电量变化对应0.02V电压变化（线性近似）。这样你就能用简单的线性关系来计算误差。

  • 调整预测：
    你根据误差（0.05%）调整你的预测模型，比如稍微调整一下“玩游戏时每小时掉电15%”这个参数，变成14.9%，这样下次预测会更准。

比喻总结：
EKF就像一个电池管家，他根据当前用电情况预测下一刻电量，然后用实际电量读数来修正预测。为了简化计算，他把复杂的电池特性（非线性）在当前点附近用直线（线性）来近似。这样他就能快速调整预测，但前提是电池特性变化不大（比如电池没老化，温度稳定）。

2. AEKF（自适应扩展卡尔曼滤波）的详细比喻

场景： 你是一个智能电池管家，负责管理一部用了两年的手机。你发现随着电池老化，原来的电池模型（比如新电池时每小时掉电10%）已经不准了，现在同样的用电量，实际掉电更快（比如每小时掉电12%）。而且电池老化程度还在变化。

工作过程：

  • 监测误差：
    你持续记录预测值和实际值的误差。比如你预测1小时后电量从70%降到60%，但实际发现降到58%（误差2%）。你发现最近一周的预测总是比实际偏高2%左右。

  • 自适应调整：
    你意识到电池模型已经老化，需要调整。你自动降低对电池模型的信任度（因为模型不准），同时提高对实际测量值的信任度。比如原来你相信模型70%，相信测量30%；现在调整成相信模型50%，相信测量50%。

  • 动态优化：
    你根据误差大小实时调整信任比例。如果误差变大（比如预测偏高3%），你就更相信测量值（比如模型40%，测量60%）；如果误差变小（比如预测偏高1%），你就稍微增加对模型的信任（比如模型60%，测量40%）。

  • 更新模型：
    你还根据误差趋势更新电池模型参数。比如你发现电池老化导致掉电速度变快，就把模型参数从“每小时掉电10%”更新为“每小时掉电12%”。

比喻总结：
AEKF就像一个聪明的电池管家，他能发现电池老化导致模型不准，然后自动调整策略：减少对旧模型的依赖，更相信实际测量值。同时，他还会根据误差大小动态调整信任比例，并更新电池模型参数，让预测越来越准。

3. HIF（H∞滤波）的详细比喻

场景： 你是一个极端环境下的电池工程师，负责管理火星探测器的电池。火星环境恶劣，温度剧烈变化（-100℃到20℃），而且有宇宙辐射干扰电池电压读数。你的任务是确保电池电量估计绝对可靠，因为探测器一旦电量耗尽就会报废。

工作过程：

  • 最坏情况考虑：
    你不追求最精确的估计，而是确保在最坏情况下估计也不会太离谱。比如你估计电量是60%，但实际电量可能在55%-65%之间（误差±5%），你要求这个误差范围必须覆盖所有可能情况（包括极端温度和干扰）。

  • 鲁棒性设计：
    你设计了一个非常保守的估计策略：即使遇到最大干扰（比如电压读数突然波动10%），你的估计误差也不会超过5%。为了做到这点，你牺牲了一些精度——在正常情况下，你的估计可能不如其他方法精确，但绝不会出现大错误。

  • 抗干扰处理：
    当你收到一个异常的电压读数（比如突然显示电量从60%跳到50%），你不会立即相信它。你会结合历史数据和电池模型判断：如果当前温度是-100℃，电池电压确实可能突然下降，你就接受这个读数；但如果温度正常，你就认为这是干扰，忽略这个读数。

  • 安全边界：
    你总是留出安全余量。比如你估计剩余电量能支持探测器工作10小时，但你会告诉地面控制中心“只能工作8小时”，多留2小时作为缓冲，防止意外情况。

比喻总结：
HIF就像一个保守的电池工程师，他不追求最精确的估计，而是确保在最恶劣环境下估计也不会出错。他宁可牺牲一些精度，也要保证估计的可靠性。这种策略特别适合对安全性要求极高的场景，比如航天、医疗设备。

4. PF（粒子滤波）的详细比喻

场景： 你是一个侦探队长，带领100名侦探（粒子）来估算一个神秘电池的剩余电量。这个电池很特殊，它的电压和电量关系非常复杂（非线性），而且受温度、老化等多种因素影响。

工作过程：

  • 初始化侦探：
    你让100名侦探各自猜测一个电量值（比如侦探1猜50%，侦探2猜51%，…侦探100猜100%），每个侦探代表一个可能的电量状态。

  • 预测阶段：
    你告诉所有侦探：“电池正在以1A电流放电，根据电池模型，1分钟后电量会下降0.5%”。每个侦探根据这个信息更新自己的猜测（比如猜50%的侦探更新为49.5%）。

  • 测量阶段：
    1分钟后，你测量电池电压（比如3.7V），然后告诉所有侦探：“根据电压-电量对照表，3.7V对应的电量可能是48%-52%之间”。每个侦探根据这个信息评估自己的猜测有多靠谱（比如猜49.5%的侦探觉得“我在48%-52%范围内，靠谱程度80%”；猜55%的侦探觉得“我不在范围内，靠谱程度10%”）。

  • 重采样阶段：
    你淘汰掉不靠谱的侦探（比如猜55%的），让靠谱的侦探（比如猜49.5%的）“繁殖”出多个新侦探（新侦探的猜测值在原侦探附近随机波动）。这样侦探队伍就集中在最可能的电量值附近。

  • 结果输出：
    你计算所有侦探猜测的平均值（比如49.8%），作为最终的电量估计值。

比喻总结：
PF就像一个侦探队，用大量侦探（粒子）覆盖所有可能的电量状态。通过预测（根据放电模型更新猜测）和测量（根据电压读数评估靠谱程度），不断淘汰不靠谱的侦探，让靠谱的侦探“繁殖”，最终集中在最可能的电量值上。这种方法能处理非常复杂的电池特性，但需要大量计算（管理100名侦探）。

5. EKPF（扩展卡尔曼粒子滤波）的详细比喻

场景： 你是一个智能侦探队长，管理一个电池电量侦探队。你结合了EKF的快速计算和PF的高精度，用更少的侦探实现精准估计。

工作过程：

  • EKF助手分析：
    你先让一个EKF助手快速分析：“根据当前电压3.7V和放电电流1A，真实电量在49%-51%之间的概率最大”。这个助手用线性近似快速缩小了范围。

  • 高效部署侦探：
    你不需要再让侦探覆盖0%-100%的整个范围，而是只在49%-51%这个小区间内部署侦探（比如侦探1猜49.0%，侦探2猜49.1%，…侦探20猜51.0%）。这样你只需要20名侦探就能达到原来100名侦探的精度。

  • 双重优化：

    1. EKF优化： 助手用线性近似快速锁定高概率区间，节省了计算资源。
    2. PF优化： 侦探队在小范围内用粒子滤波精确估计，处理了非线性问题。

  • 结果输出：
    你计算20名侦探猜测的平均值（比如49.85%），作为最终电量估计。这个结果既精确（因为侦探集中在小范围内），又高效（因为侦探数量少）。

比喻总结：
EKPF就像一个智能侦探队，先用EKF助手快速锁定高概率区间（比如49%-51%），然后在这个小区间内部署少量侦探（20名）进行精确估计。这样既保持了PF的高精度（能处理复杂非线性），又大大减少了计算量（因为侦探数量少）。它结合了EKF的效率和PF的精度，特别适合需要高精度但计算资源有限的场景（比如高端电动车）。

1.共有初始化部分

n = 4;  % 状态维度
N = length(t);
Q = 0.000000000001; % 过程方差
W = sqrt(Q)*randn(n,N); 
R = 0.01;  % 测量方差
V = sqrt(R)*randn(1,N);
s = [0;0;0;1]; 
x = [0;0;0;0.6];
xV = zeros(n,N); % 最优估计值
sV = zeros(n,N); % 真实值
zV = zeros(n,N); % 状态测量值
zIV = zeros(n,N); % 电流激励
z1v = zeros(1,N);
  • 状态维度：n=4，表示状态向量有4个分量（RC网络的电压、SOC）。
  • 时间点数：N，由时间向量t的长度决定。
  • 过程噪声方差：Q非常小（1e-12），说明过程噪声很小。
  • 测量噪声方差：R=0.01，相对较大。
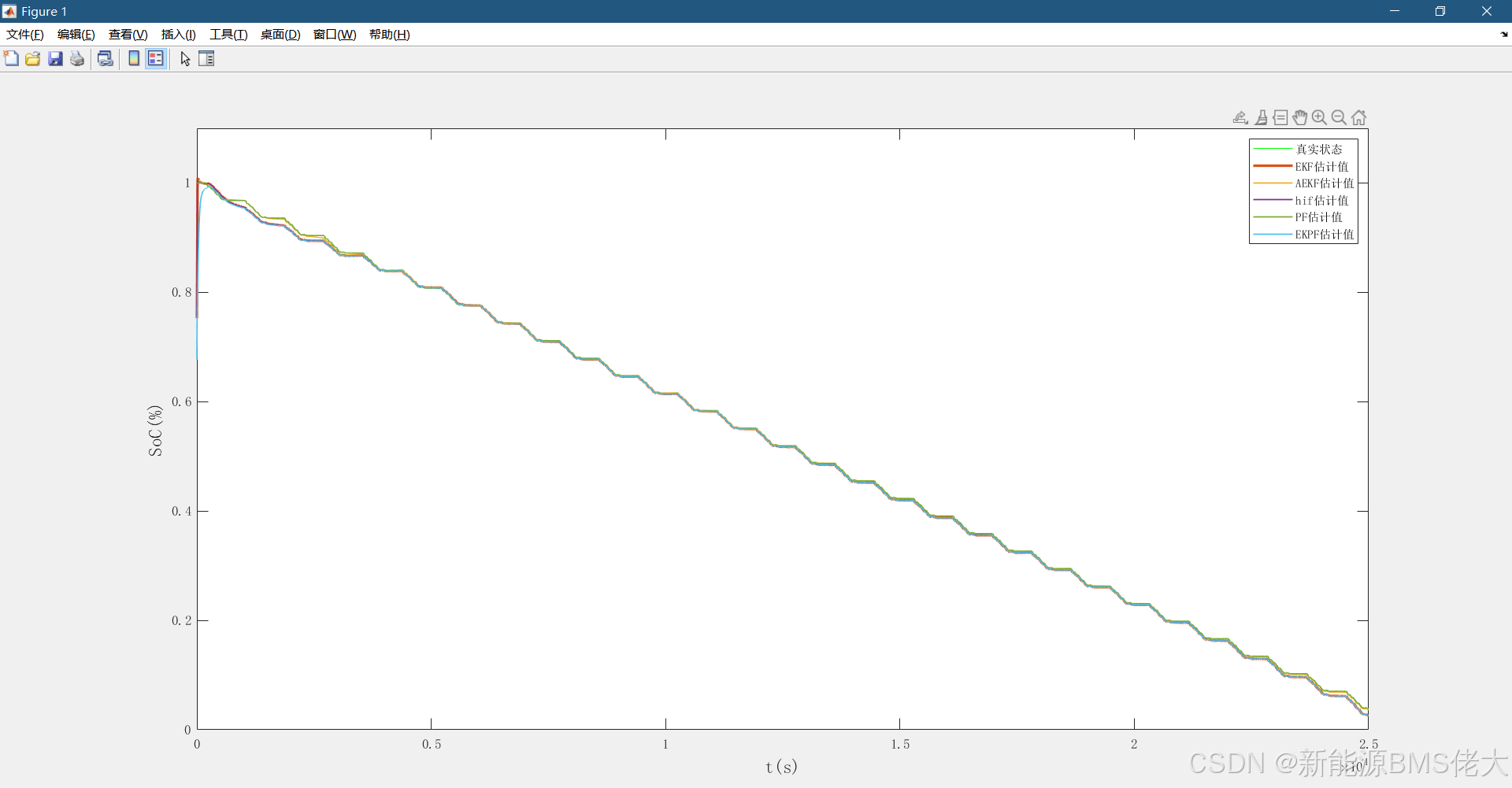
  • 真实状态初始值：s=[0;0;0;1]，其中最后一个分量（SOC）初始为1（100%）。表示从满电开始进行放电。
  • 估计状态初始值：x=[0;0;0;0.6]，SOC初始估计为0.6（60%）。
  • 存储变量：xV（估计值）、sV（真实值）、zV（测量值）、zIV（电流激励）、z1v（可能用于存储端电压估计值）。

2.EKF初始化

P_ekf = eye(n);

3.AEKF初始化

  • 协方差矩阵初始化：P_ekf为单位矩阵，表示初始状态估计的不确定性。
q0 = zeros(n,1); % 更新的状态噪音
r0 = 1; % 更新的测量噪音
b = 0.97; % sage-husa更新用
T = 0.01*eye(n);
P_aekf = eye(n);
  • 自适应参数：q0（状态噪声初始估计）、r0（测量噪声初始估计）、b（遗忘因子，用于Sage-Husa自适应滤波）。
  • T矩阵：用于噪声更新的协方差矩阵。
  • 协方差矩阵：P_aekf初始化为单位矩阵。

4.HIF初始化

L = 0.1;  %倒数是边界,但是L越大，K越小，失去纠偏能力
%S = [0.2 0 0 0;0 0.2 0 0;0 0 0.2 0;0 0 0 0.5];                %未知  
S=1;
P_hif = eye(n);
  • L：H_inf滤波器的性能边界参数，L越大，滤波器增益越小，纠偏能力越弱。
  • S：H_inf滤波器的权重矩阵，这里设为1（标量），也可以是对角矩阵。
  • P_hif：HIF的初始协方差矩阵，单位矩阵。

5. PF初始化

x1 = [0;0;0;1];
NN = 100;
Nth =100; %重采样阈值
xhatPart = x1;
P_pf = eye(n);
xpart = zeros(n,NN);
xhatPartArr = zeros(n,N); %存储估计的SOC值
xpartminus = zeros(n,NN);
for i = 1 : NNxpart(:,i) = x1 + sqrt(Q)* randn(n,1);
end
  • x1：PF的初始状态估计，设为[0;0;0;1]（SOC=100%）。
  • NN：粒子数，100个。
  • Nth：重采样阈值，当有效粒子数低于此值时进行重采样。
  • xhatPart：当前的状态估计（单个粒子）。
  • P_pf：PF的初始协方差矩阵，单位矩阵。
  • xpart：粒子矩阵，每列代表一个粒子的状态。
  • xhatPartArr：存储每个时间步的状态估计（用于后续绘图）。
  • xpartminus：预测步的粒子矩阵。
  • 循环初始化粒子：每个粒子由初始状态加上高斯噪声（均值为0，标准差为sqrt(Q)）生成。

6. EKPF初始化

R_ekpf =2;
ekpfxhatPart = x;
ekpfxpart = zeros(n,NN);
ekpfp = zeros(n,n,NN);
ekpfxhatPartArr = zeros(n,N); %存储估计的SOC值
z1v_ekpf = zeros(1,N);
for i = 1 : NNekpfxpart(:,i) = x + sqrt(Q)* randn(n,1);ekpfp(:,:,i) = eye(n);
end
ekpfpupdate = ekpfp;
ekpfxpartupdate = ekpfxpart;
  • R_ekpf：EKPF的测量噪声方差，设为2。
  • ekpfxhatPart：EKPF的初始状态估计，设为x（[0;0;0;0.6]）。
  • ekpfxpart：粒子矩阵，初始化方式与PF类似。
  • ekpfp：每个粒子的协方差矩阵，三维矩阵（n×n×NN），初始为单位矩阵。
  • ekpfxhatPartArr：存储状态估计。
  • z1v_ekpf：存储EKPF的端电压估计。
  • 循环初始化粒子和协方差矩阵。
  • ekpfpupdate和ekpfxpartupdate：更新后的粒子和协方差矩阵。

7. 初始函数（定义电池模型）

R0 = @(x)(-0.07495*(x(4))^4+0.2187*(x(4))^3-0.1729*(x(4))^2+0.01904*(x(4))+0.1973);
R1 = @(x)(0.07826*(x(4))^4-0.2208*(x(4))^3+0.217*(x(4))^2-0.08761*(x(4))+0.01664);
R2 = @(x)(0.1248*(x(4))^4-0.2545*(x(4))^3+0.1254*(x(4))^2-0.03868*(x(4))+0.05978);
C1 = @(x)(2431*(x(4))^4-4606*(x(4))^3+3084*(x(4))^2-589*(x(4))+209.8);
C2 = @(x)(681.1*(x(4))^4-3197*(x(4))^3+4595*(x(4))^2-3114*(x(4))+1444);
U_HPPC_OCV = @(x)(4.715*(x(4))^5-14.53*(x(4))^4+16.32*(x(4))^3-8.031*(x(4))^2+2.438*(x(4))+3.247);
U_OCV = @(x)(0.008488*(x(4))^5-0.03224*(x(4))^4+0.004118*(x(4))^3+0.06053*(x(4))^2+0.2167*(x(4))+3.683);
h = @(x)(4.715*(x(4))^5-14.53*(x(4))^4+16.32*(x(4))^3-8.031*(x(4))^2+2.438*(x(4))+3.247-x(3)-x(2)-x(1));  % 测量方程A = [0 0 0 0;0 exp(-1/(R1(x)*C1(x))) 0 0;0 0 exp(-1/(R2(x)*C2(x))) 0;0 0 0 1]; 
B = [R0(x);R1(x)*(1-exp(-1/(R1(x)*C1(x))));R2(x)*(1-exp(-1/(R2(x)*C2(x))));-1/3.18/3600];
As = [0 0 0 0;0 exp(-1/(R1(s)*C1(s))) 0 0;0 0 exp(-1/(R2(s)*C2(s))) 0;0 0 0 1];
Bs = [R0(s);R1(s)*(1-exp(-1/(R1(s)*C1(s))));R2(s)*(1-exp(-1/(R2(s)*C2(s))));-1/3.18/3600];
  • 定义了电池模型的参数（R0, R1, R2, C1, C2）和OCV（开路电压）函数，它们都是SoC（x(4)）的函数。
  • h：测量方程，计算端电压（OCV减去两个RC网络的电压降）。
  • A和B：状态方程的系数矩阵，依赖于当前状态x（特别是SoC）。状态方程为：x_k = Ax_{k-1} + BI_k + w_k，其中I_k是电流。
  • As和Bs：使用真实状态s计算的系数矩阵，用于生成真实状态序列。

8. 真实值估计

sV = sV_fucn(As,Bs,s,sV,N,I,Q,n);
  • 调用函数sV_fucn生成真实状态序列sV，使用真实模型（As, Bs）和初始状态s，并加入过程噪声。

9. 加入算法（运行各种滤波器）

[xV,z,z1v] = EKF_fucn(n,Q,R,I,z,x,P_ekf,xV,zV,zIV,z1v,A,B,h,N);
[xV_aekf,z_aekf,z1v_aekf] = AEKF_fucn(n,Q,R,q0,r0,I,z,x,P_aekf,xV,zV,zIV,z1v,b,T,A,B,h,N);
[xV_hif,z_hif,z1v_hif] = HIF_fucn(n,Q,R,z,x,P_hif,xV,zV,zIV,z1v,L,S,A,B,h,N,I);
[xV_pf,z1v_pf] = PF_fucn(n,Q,R,W,t,I,z,x1,P_pf,xpart,xhatPartArr,xhatPart,xpartminus,z1v,N,NN,Nth,A,B,h);
[xV_ekpf,zlv_ekpf] = EKPF_fucn(n,Q,R_ekpf,I,z,x,ekpfp,ekpfxpart,ekpfxhatPartArr,ekpfxhatPart,ekpfxpartupdate,z1v,N,NN,Nth,A,B,h);
  • 分别调用五种滤波算法的函数：EKF、AEKF、HIF、PF、EKPF。
  • 每个函数返回状态估计序列（如xV）和端电压估计序列（如z1v）。

10. 计算安时积分法的SOC（作为对比）

soc = zeros(1,N);
soc(1) = 1;
for k = 2:Nsoc(k) = soc(k-1)+I(k)/3.18/3600;
end
  • 安时积分法计算SoC：初始SoC为1，然后根据电流积分（除以容量3.18Ah和时间单位转换3600）更新SoC。

11. 误差分析

% RMSE
RMSE_AH = sqrt(sum((soc-sV(4,:)).^2)/N);
RMSE_EKF = sqrt(sum((xV(4,:)-sV(4,:)).^2)/N);
RMSE_AEKF = sqrt(sum((xV_aekf(4,:)-sV(4,:)).^2)/N);
RMSE_HIF = sqrt(sum((xV_hif(4,:)-sV(4,:)).^2)/N);
RMSE_PF = sqrt(sum((xV_pf(4,:)-sV(4,:)).^2)/N);
RMSE = [RMSE_EKF,RMSE_AEKF,RMSE_HIF,RMSE_PF]';
RMSE_EKPF = sqrt(sum((xV_ekpf(4,:)-sV(4,:)).^2)/N);
% MAE
MAE_AH = sum(abs(soc-sV(4,:)))/N;
MAE_EKF = sum(abs(xV(4,:)-sV(4,:)))/N;
MAE_AEKF = sum(abs(xV_aekf(4,:)-sV(4,:)))/N;
MAE_HIF = sum(abs(xV_hif(4,:)-sV(4,:)))/N;
MAE_PF = sum(abs(xV_pf(4,:)-sV(4,:)))/N;
MAE = [MAE_EKF,MAE_AEKF,MAE_HIF,MAE_PF]';
MAE_EKPF = sum(abs(xV_ekpf(4,:)-sV(4,:)))/N;
% MAXE
MAXE_AH = max(abs(soc-sV(4,:)));
MAXE_EKF = max(abs(xV(4,:)-sV(4,:)));
MAXE_AEKF = max(abs(xV_aekf(4,:)-sV(4,:)));
MAXE_HIF = max(abs(xV_hif(4,:)-sV(4,:)));
MAXE_PF = max(abs(xV_pf(4,:)-sV(4,:)));
MAXE = [MAXE_EKF,MAXE_AEKF,MAXE_HIF,MAXE_PF]';
MAXE_EKPF = max(abs(xV_ekpf(4,:)-sV(4,:)));
  • 计算安时积分法（AH）和五种滤波算法的SoC估计的均方根误差（RMSE）、平均绝对误差（MAE）和最大误差（MAXE）。

12. 绘制图形

  • 代码中包含多个figure，分别绘制：

  • Figure 1：真实SoC和各算法估计的SoC随时间变化曲线
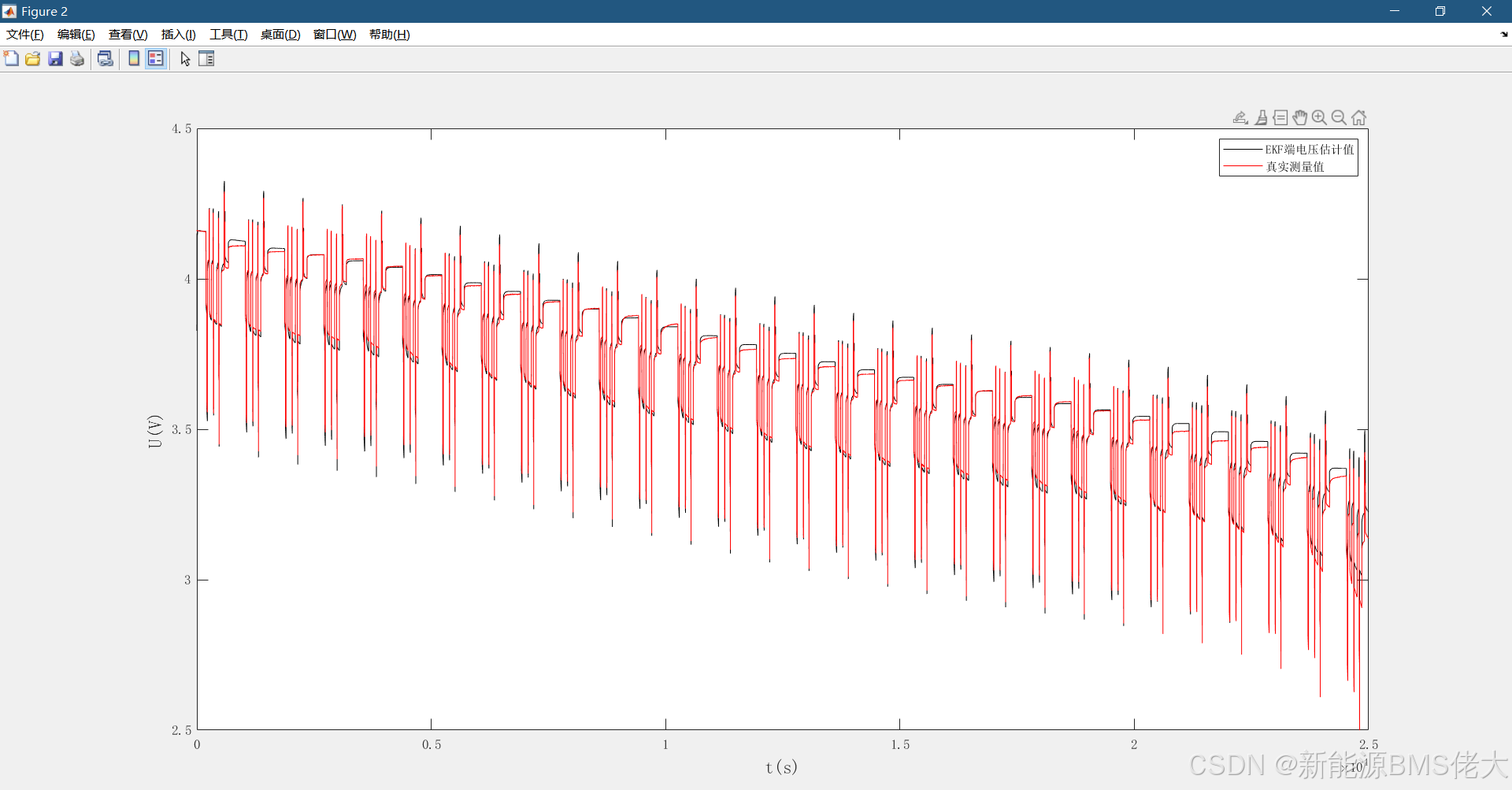
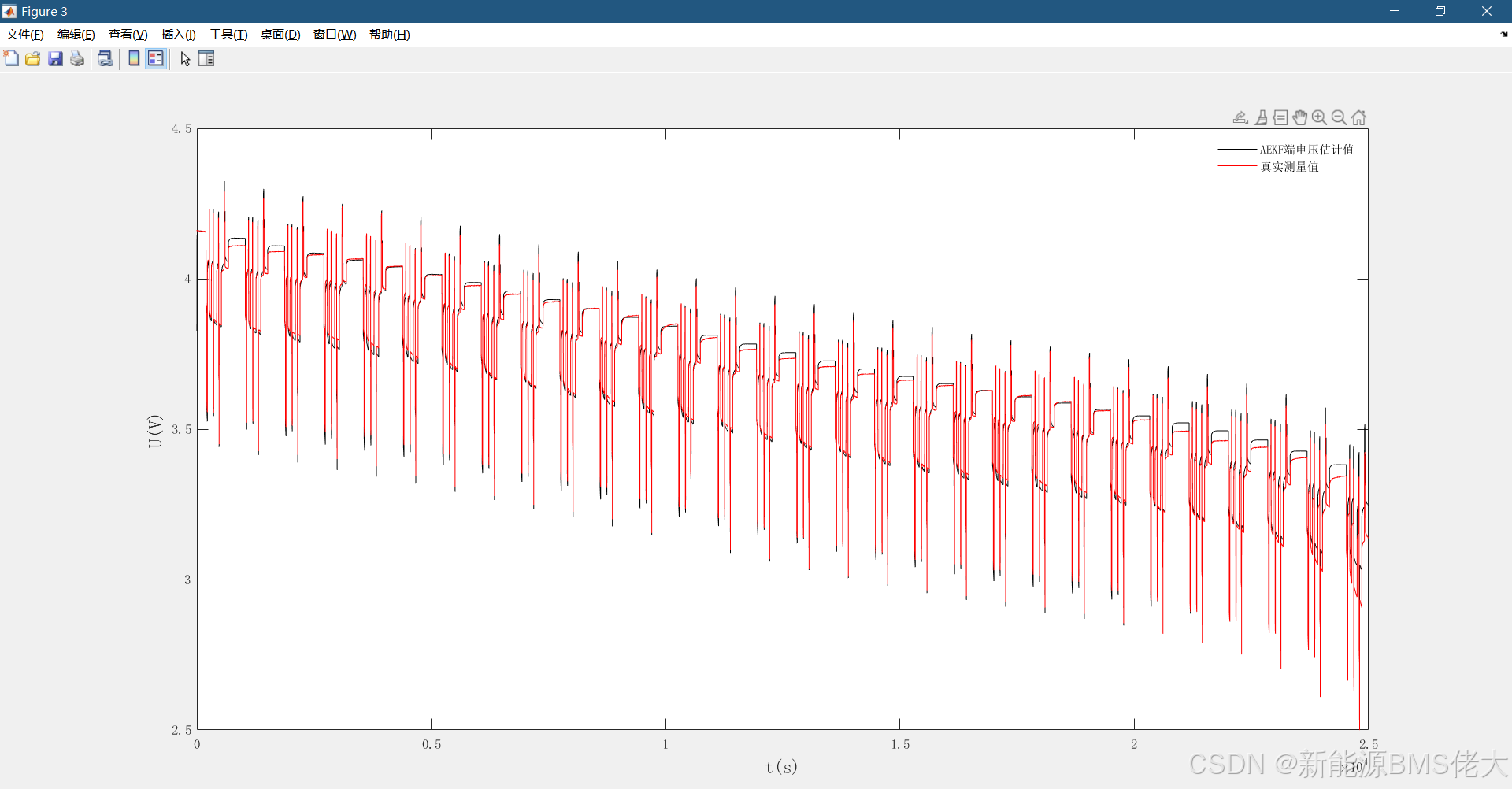
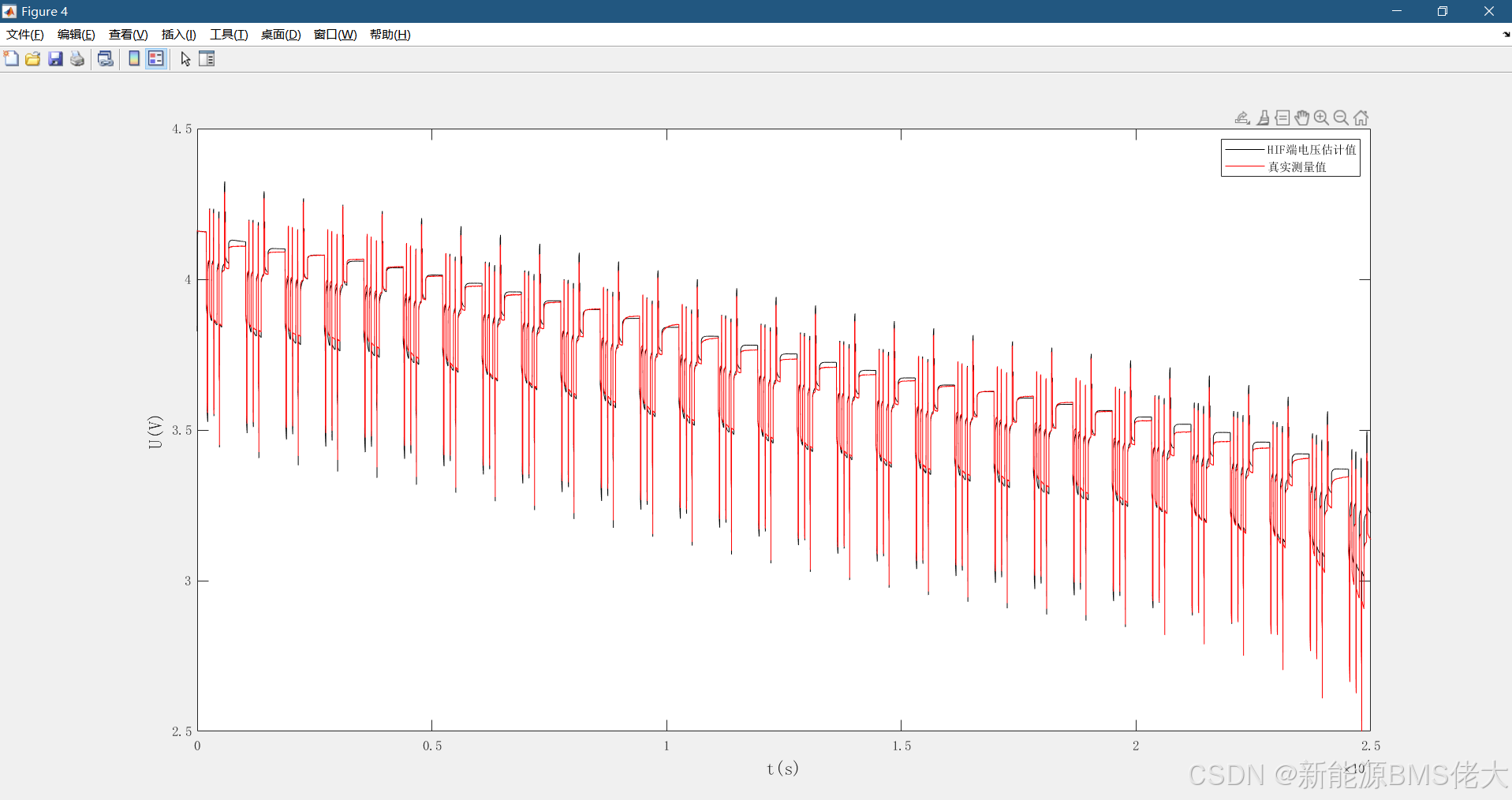
  • Figure 2-5：EKF、AEKF、HIF、PF估计的端电压与真实测量值的对比
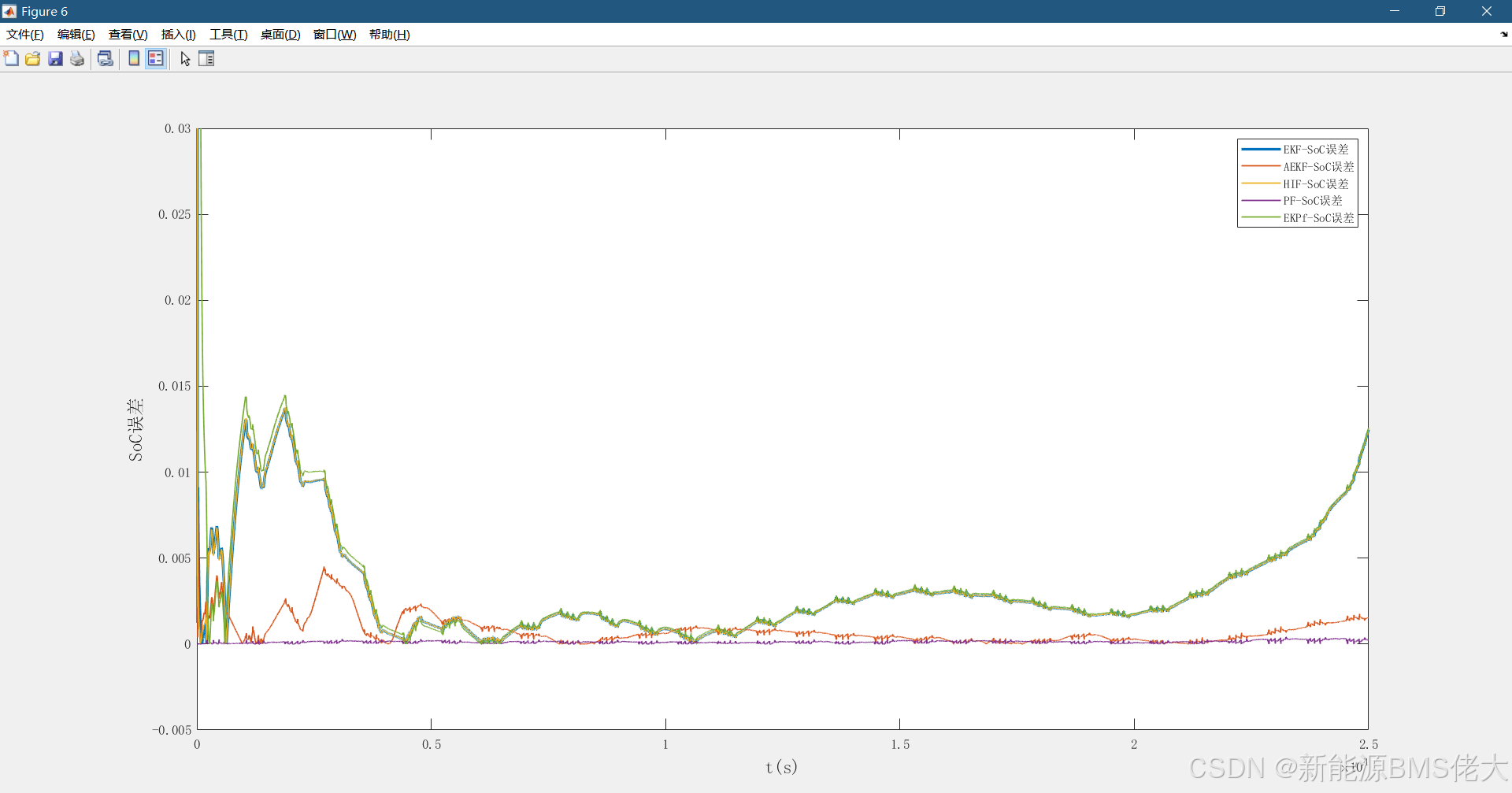
  • Figure 6：各算法SoC估计的绝对误差
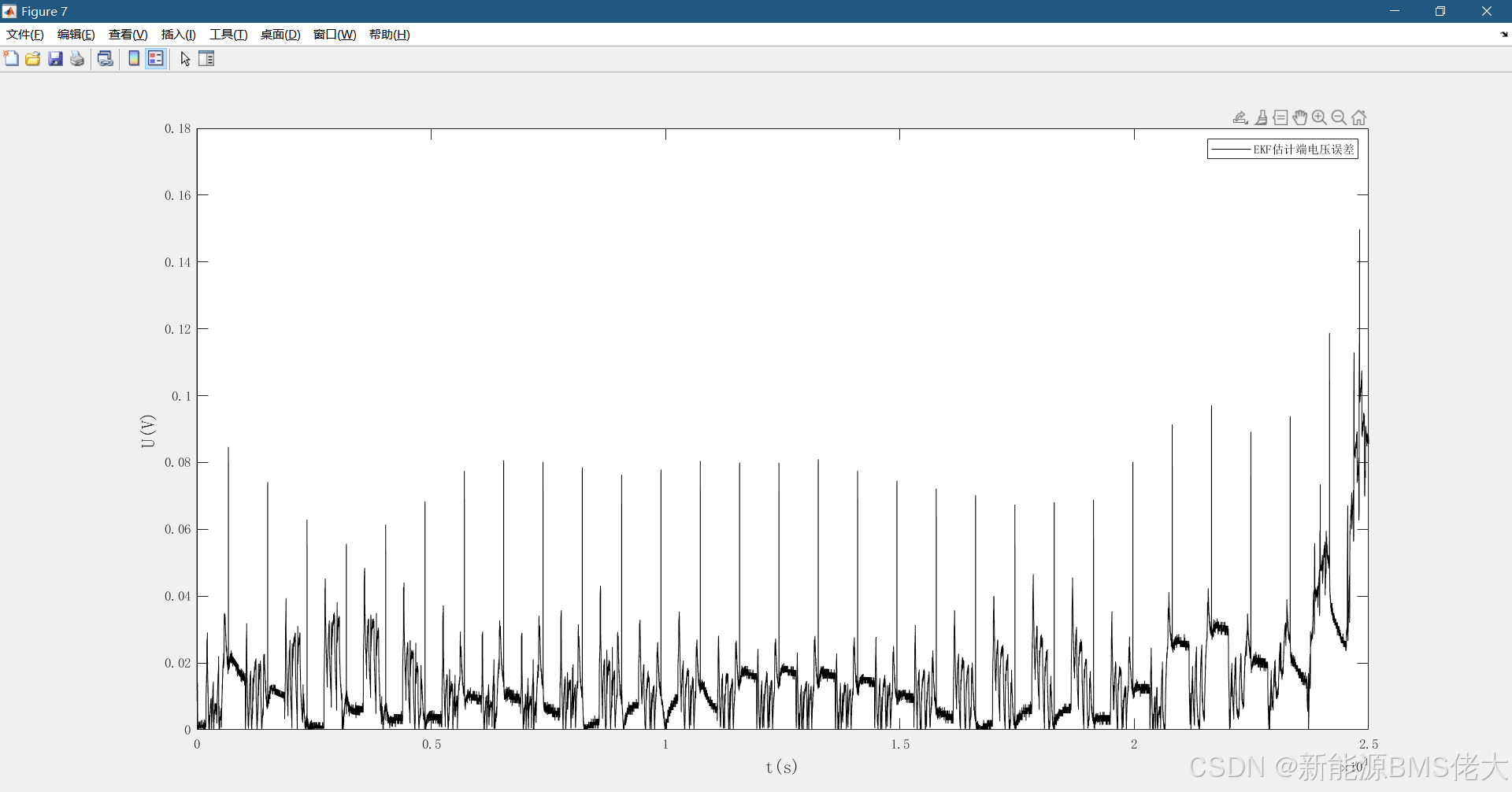
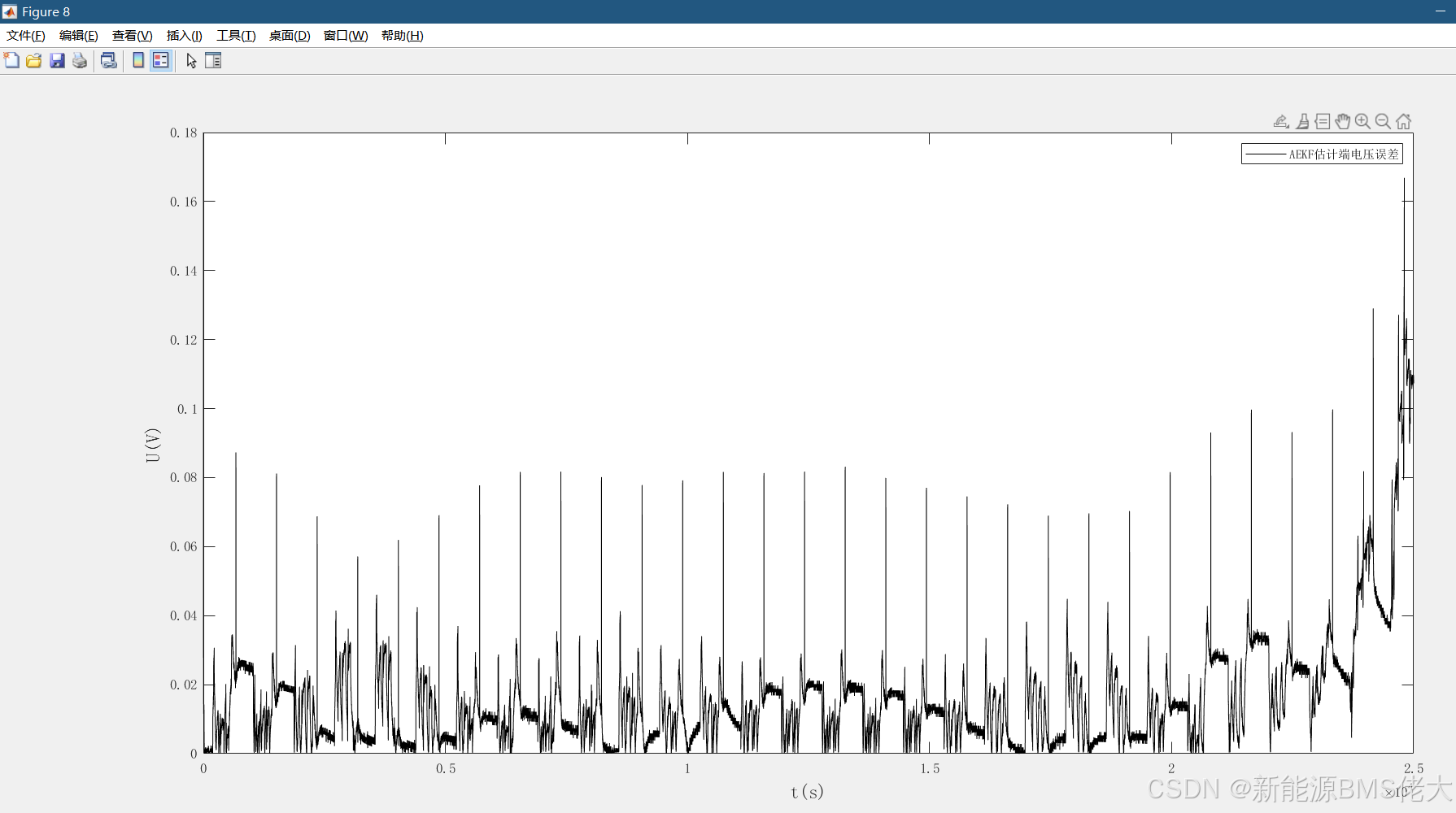
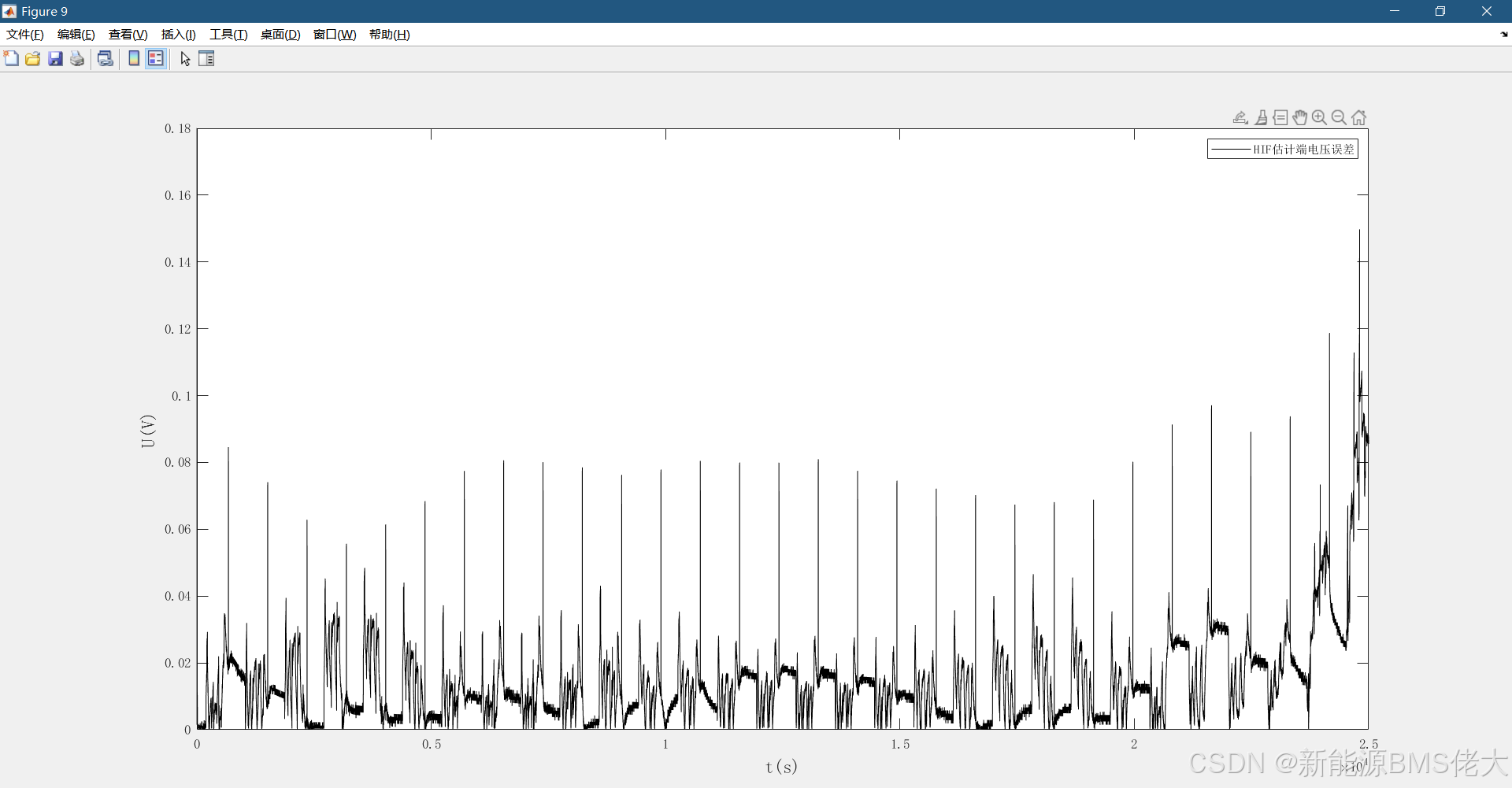
  • Figure 7-10：EKF、AEKF、HIF、PF端电压估计的绝对误差

相关代码模型资料点赞评论关注后吗，私信我获取。

http://www.dtcms.com/a/333137.html

相关文章：

  • TDengine IDMP 高级功能（2. 事件模板）
  • Stability AI技术浅析（二）：LDM
  • 【国内电子数据取证厂商龙信科技】如何识别与查杀木马程序
  • 音视频面试题集锦第 23 期
  • 应急救援智能接处警系统——科技赋能应急，筑牢安全防线
  • Day60--图论--94. 城市间货物运输 I（卡码网），95. 城市间货物运输 II（卡码网），96. 城市间货物运输 III（卡码网）
  • PaddleNLP进行Bart文本摘要训练
  • Linux系统——进程与线程
  • PyTorch 进行人脸训练和 Java 实现人脸识别的解决方案
  • 权重迁移笔记
  • Android RxJava 过滤与条件操作详解
  • CPU性能篇-系统的软中断CPU使用率升高如何处理-Day 06
  • Pytest项目_day16（yaml和parametrize结合）
  • 【R语言】更换电脑后，如何在新设备上快速下载原来设备的 R 包？
  • 神经网络、深度学习与自然语言处理
  • Linux程序内存布局分析
  • ROS2 setup.bash和setup.sh区别差异
  • 【JAVA】实现word添加标签实现系统自动填入字段
  • Python匿名函数的具体用法
  • 堕落之主 单机+联机 全DLC 送修改器（Lords of the Fallen）免安装中文版
  • 【机器人-基础知识】ROS常见功能架构
  • 【JAVA高级】实现word转pdf 实现，源码概述。深坑总结
  • JavaScript（JS）DOM（四）
  • 提词器电脑版哪个好用？芦笋提词器优势评测与下载
  • 算法02 二进制与位运算
  • 解锁AI大模型：Prompt工程全面解析
  • 迭代器模式C++
  • Unity中 terriaria草，在摄像机拉远的时候就看不见了，该怎么解决
  • week1-[循环嵌套]蛇
  • 低资源语言翻译：数据增强与跨语言迁移学习策略