01数据结构-拓扑排序

1.基础概念

• 1.什么是活动

  所有的工程或者某种流程都可以分为若干个小的工程或者阶段，我们称这些小的工程或阶段为“活动”。打个比方，如何把一只大象装到冰箱里，很简单，分三步。第一，打开冰箱⻔；第二，将大象装进去；第三，关上冰箱⻔。这三步中的每一步便是一个 “活动” 。

• 2.什么是有向无环图？

  一个无环的有向图 称为 有向无环图（Directed Acycline Graph），简称 DAG 图。（这不等于没说吗？）所以直接看图。

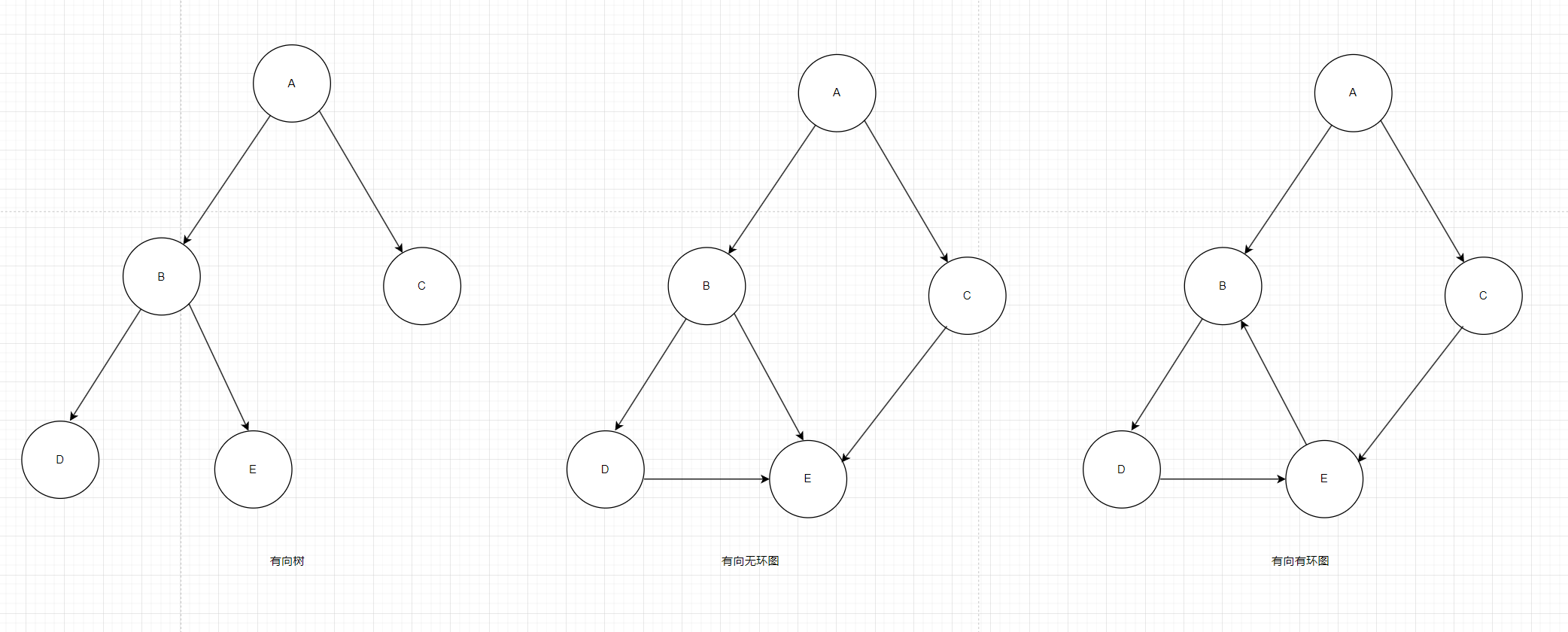
图1

图中最左边的是有向树，中间的是有向无环图，最右则的是有向图（因为图中BED三个顶点之间构成一个有向环）。

• 3.什么是AOV网？

  在一个表示工程的有向图中，用 顶点表示活动，用弧表示活动之间的优先关系的有向图 称为顶点表示活动的网（Activity On Vertex Network），简称AOV网。

  日常生活中，一项大的工程可以看作是由若干个子工程组成的集合，这些子工程之间必定存在一定的先后顺序，即某些子工程必须在其他的一些子工程完成后才能开始。

  AOV网中的弧表示活动之间存在的某种制约关系，比如上面说到将大象装入冰箱，必须先打开冰箱⻔，才能将大象装进去，大象装进去才能关上冰箱⻔，从而完成我们的任务。还有一个经典的例子那就是选课，通常我们是学了C语言程序设计，才能学习数据结构，这里的制约关系就是课程之间的优先关系。（之后我们会讲一个完整的例子，大家就会更清楚AOV网）。

• 4.什么是拓扑序列？

  设G=(V,E)是一个具有n个顶点的有向图，V中的顶点序列 V1,V2,V3…Vn满足若从顶点Vi到Vj有一条路径，则在顶点序列中顶点Vi必在顶点Vj之前。则我们称这样的顶点序列为一个拓扑序列。

• 5.什么是拓扑排序

  拓扑排序就是对一个有向无环图构造拓扑序列的过程。

  例如：一个项目包括A,B,C,D四个子部分来完成，并且A依赖于B和D，C依赖于D，现在要指定一个计划，写出A,B,C,D的执行顺序，这时就可以用到拓扑排序，它就是用来确定事务发生的顺序的。

  在拓扑排序中如果存在一条从顶点A到顶点B的路径，那么在排序结果中B就在A的后面。

2.拓扑排序

2.1拓扑排序逻辑思想

• 1找到图中，入度为0(没有前驱)的顶点，把这些顶点放入缓存区(栈,队列)，我们一般推荐栈来当我们的缓存区，虽然队列和我们现实世界的逻辑很像，但是队列要维护两个指针，栈只需要维护一个指针。
• 2从缓存区中取出一个顶点，放入结果集。这个顶点的任务执行完毕。
• 3这个顶点的出度对应的其余顶点的入度清0。
• 4再次查找入度为0的点，如果有继续放入缓存区
• 5重复2-3-4
• 6 缓存区为空时判断结果集中的顶点个数和实际图中顶点的个数相比，若相等则没有环。

2.2拓扑排序算法模拟

我们需要知道图中各个的入度顶点，由于还是有向图还需要知道入度我们很容易想到应该用邻接表来存任意图。

如图2，我们用邻接表来存图，创建一个一维数组表示顶点的入度值，初始化时所有的入度值都为0，在遍历邻接表的时侯，例如0能出到1，2，3，就给顶点1，2，3的入度加1。1能到2，4就给2，4顶点的入度加1，一直到遍历完所有顶点，就算时把这个图的所有顶点的初始时的入度值计算好了。

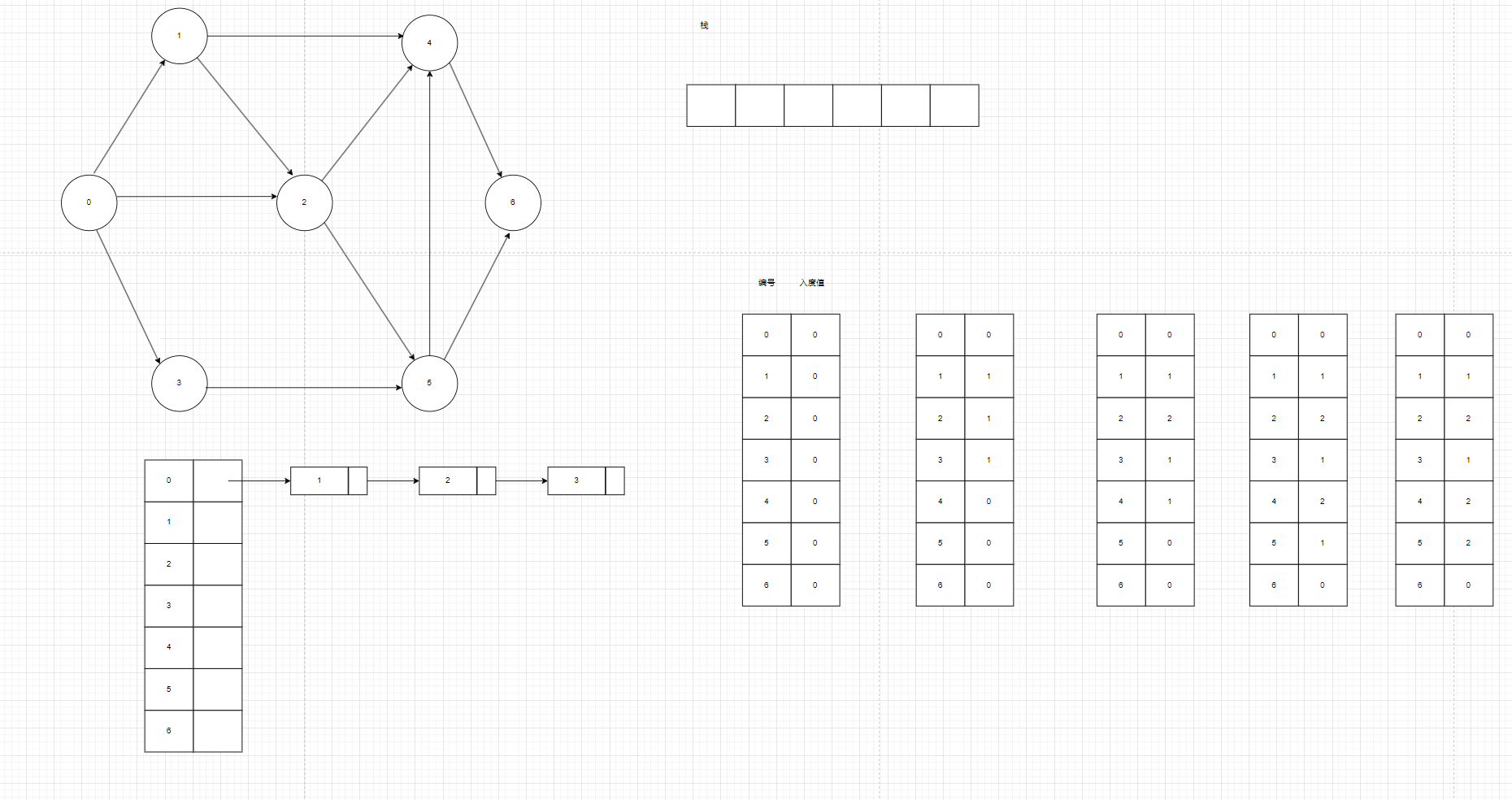
图2

找到数组中入度值为0的点，把它放入缓存区中，弹栈到结果集并在数组中对应的入度值-1。

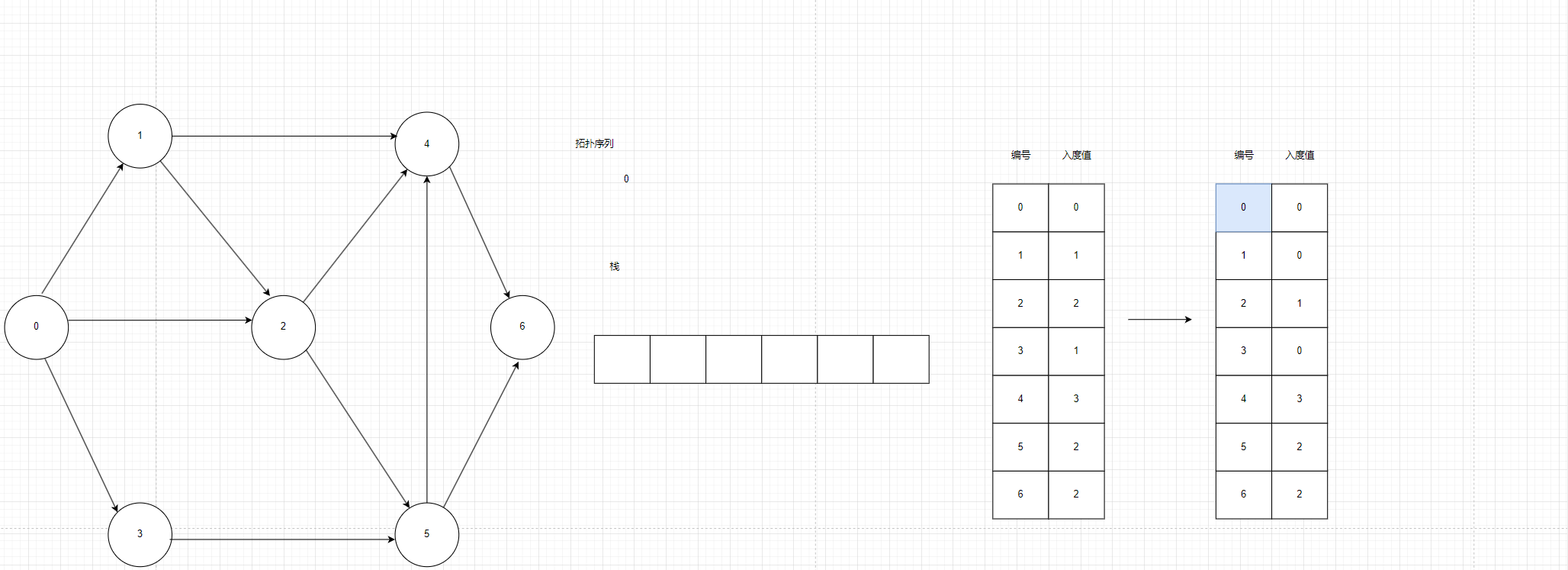
图3

把1，3放进缓存区，弹1到结果集中并在数组中对应的入度值-1。在弹栈的过程中若发现有入度为0的就顶点就弹入缓存区中。

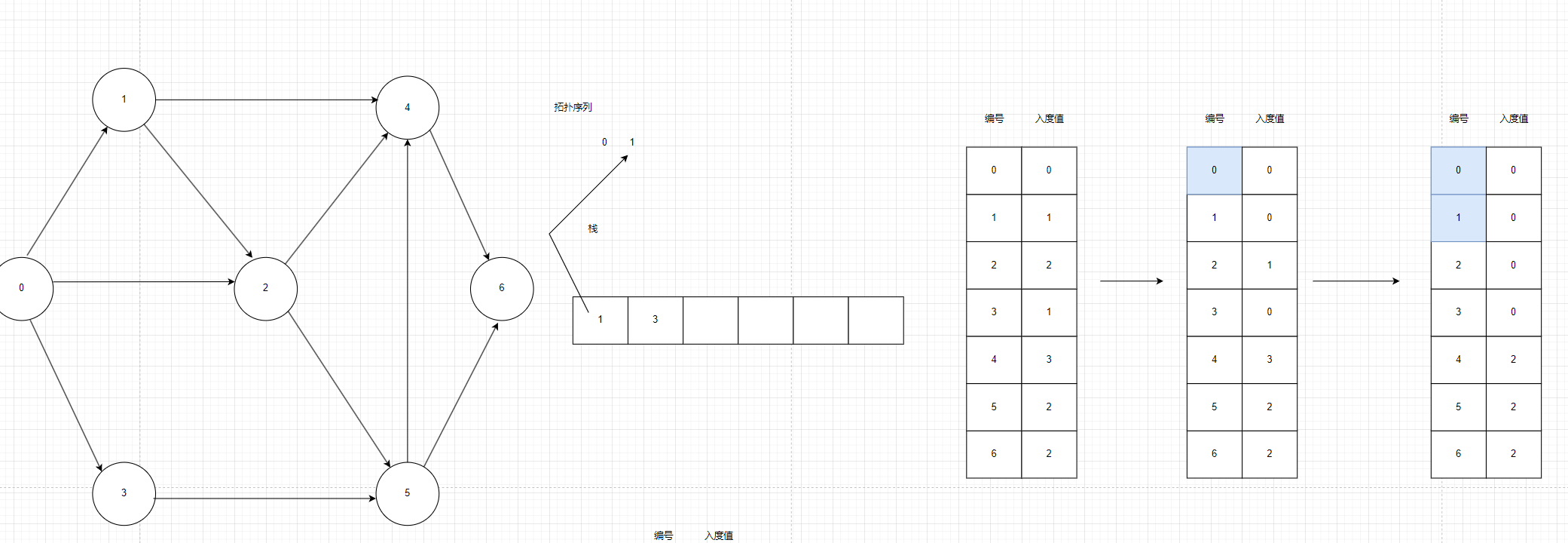
图4

重复上述操作，一直处理完所有的顶点。

2.3拓扑排序代码实现

拓扑排序核心接口实现:int TopologicalSortAGrap(const AGraph *graph)；

#include "topologicalSort.h"
#include <stdlib.h>
#include <string.h>int TopologicalSortAGrap(const AGraph *graph) {//记录结果集中的顶点数int count=0;// 定义一个入度记录表，便于发现入度为0时，放入缓存区int * inDegree = malloc(sizeof(int) * graph->nodeNum);if (inDegree == NULL) {return -1;}memset(inDegree, 0, sizeof(int) * graph->nodeNum);// 初始化入度记录表for (int i = 0; i < graph->nodeNum; ++i) {if (graph->nodes[i].firstEdge) {ArcEdge *edge=graph->nodes[i].firstEdge;while (edge) {++inDegree[edge->no];edge=edge->next;}}}// 查找入度记录表，度为0的顶点，设计一个链式栈的缓存区，更新入度记录表时，发现0，就放入任务栈int *stack = malloc(sizeof(int) * graph->nodeNum);if (stack == NULL) {free(stack);return -1;}int top = -1;for (int i = 0; i < graph->nodeNum; ++i) {if (inDegree[i] == 0) {stack[++top] = i;}}// 根据任务栈里的数据，弹出第一个任务，这个任务对应的节点相关的入边个数删除// 更新入度记录表，如果更新过程中，发现入度为0，直接入栈while (top != -1) {//出度循环逻辑部分int index=stack[top];--top;ArcEdge *edge=graph->nodes[index].firstEdge;visitAGraphNode(&graph->nodes[index]);while (edge) {--inDegree[edge->no];if (inDegree[edge->no] == 0) {stack[++top] = edge->no;}edge=edge->next;}++count;}free(stack);free(inDegree);//判断是否有环，1表示有向有环，0表示无环，-1表示错误return count==graph->nodeNum?0:1;
}

这里就是把2.1和2.2的逻辑用代码实现了一下，大家应该能看懂。

最后测一下:

#include <stdio.h>
#include "topologicalSort.h"
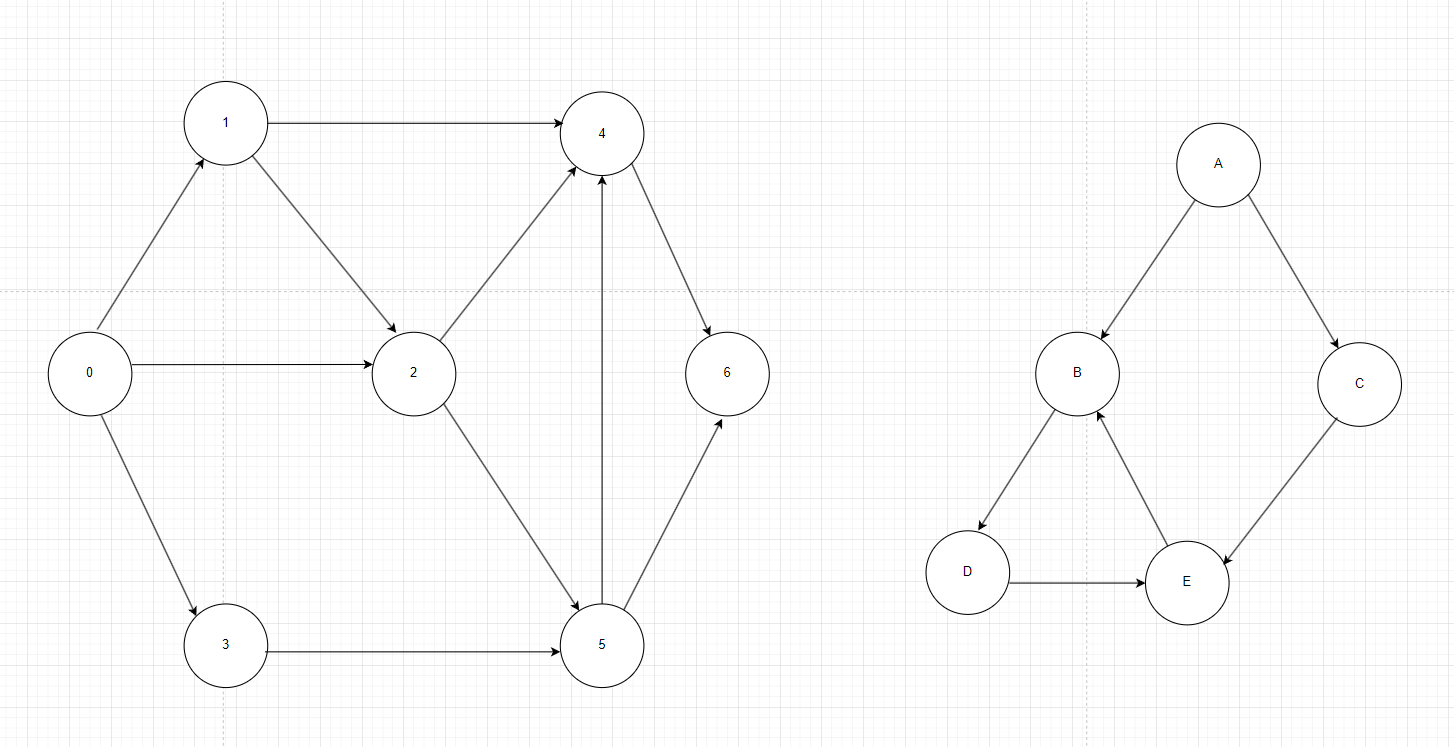
AGraph *createAGraph1() {char *names[] = {"0", "1", "2", "3", "4", "5", "6"};int n = sizeof(names)/sizeof(names[0]);AGraph *graph = createAGraph(n);if (graph == NULL) {return NULL;}initAGraph(graph, names, n, 1);addAGraph(graph, 0, 1, 1);addAGraph(graph, 0, 2, 1);addAGraph(graph, 0, 3, 1);addAGraph(graph, 1, 2, 1);addAGraph(graph, 1, 4, 1);addAGraph(graph, 2, 4, 1);addAGraph(graph, 2, 5, 1);addAGraph(graph, 3, 5, 1);addAGraph(graph, 4, 6, 1);addAGraph(graph, 5, 4, 1);addAGraph(graph, 5, 6, 1);return graph;
}AGraph *createAGraph2() {//                0    1    2    3    4char *names[] = {"A", "B", "C", "D", "E"};int n = sizeof(names)/sizeof(names[0]);AGraph *graph = createAGraph(n);if (graph == NULL) {return NULL;}initAGraph(graph, names, n, 1);addAGraph(graph, 0, 1, 1);addAGraph(graph, 0, 2, 1);addAGraph(graph, 1, 3, 1);addAGraph(graph, 2, 4, 1);addAGraph(graph, 3, 4, 1);addAGraph(graph, 4, 1, 1);return graph;
}int main() {AGraph *graph1 = createAGraph1();AGraph *graph2 = createAGraph2();int result1 = TopologicalSortAGrap(graph1);printf("\nresult1 is %d\n", result1);printf("=================\n");int result2 = TopologicalSortAGrap(graph2);printf("\nresult2 is %d\n", result2);return 0;
}

这里写了两个测试用例，一个是有向无环图，一个是有向有环图。

结果:

D:\work\DataStruct\cmake-build-debug\03_GraphStruct\TopSort.exe
0       1       2       3       5       4       6
result1 is 0
=================
A       C
result2 is 1进程已结束，退出代码为 0

大概先写这些吧，今天的博客就先写到这，谢谢您的观看。